Бланк завдання

Вихідні дані згідно індивідуального завдання:

1. Статистична обробка результатів експериментальних досліджень

§1.1. Визначення основних статистичних характеристики отриманої вибірки міцності будівельного матеріалу

Для нормування міцності будівельного матеріалу нам необхідно визначити основні статистичні характеристики, зокрема:

1) Математичне очікування:

;

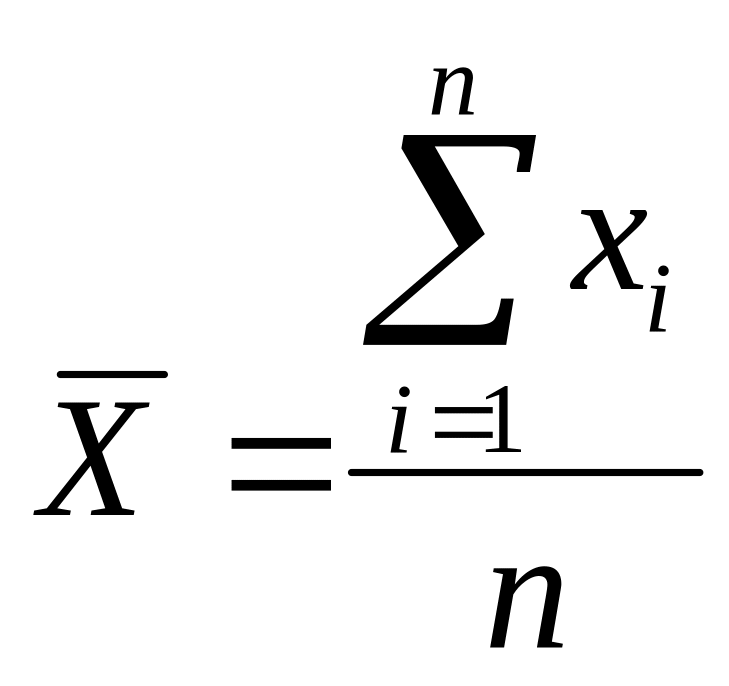2) Дисперсія:

;

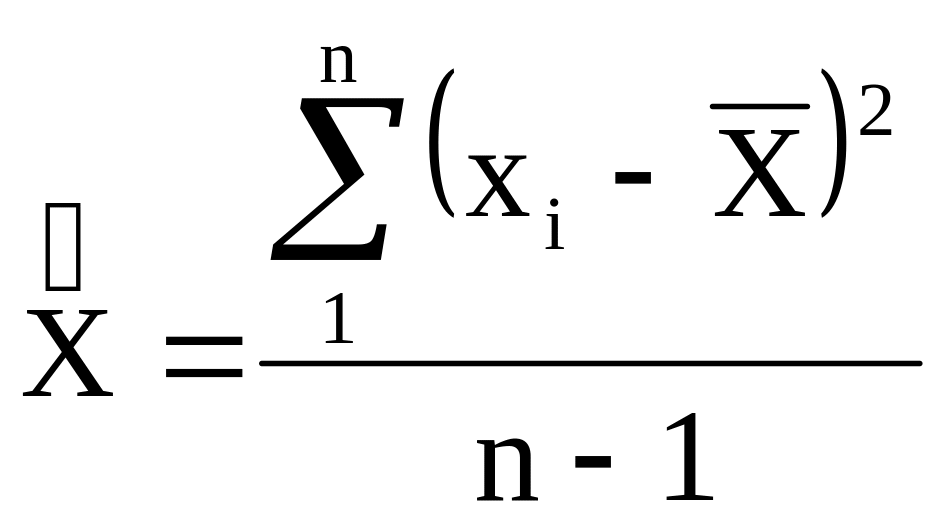3) Стандарт:

;

4) Коефіцієнт варіації: .

Використавши формули статистичної обробки, автоматизуємо визначення основних статистичних характеристик та представимо результати у таблиці MSExcel для перших двадцяти значень із сотні даних:

Примітка: значення випадкових величин міцності наведені у (кН/см²)

Коефіцієнт варіації, який характеризує ступінь мінливості міцності будівельного матеріалу визначаємо як:

.

§1.2. Побудова гістограм розподілу щільності ймовірностей міцності будівельного матеріалу

Поняття розподілу випадкових величин є одним з основних у теорії ймовірностей і математичної статистики. Співвідношення, що встановлюють зв’язок між можливими значеннями випадкової величини і відповідними до них імовірностями, називають законом розподілу випадкової величини. Для неперервних випадклвих величин закон розподілу описують функціями розподілу та щільності розподілу. Графік щільності розподілу називають кривою розподілу.

Для візуального оцінювання закону розподілу дослідженого будівельного матеріалу побудуємо гістограми, для цього розглянемо інтервальне упорядкування статистичного масиву. Групуючи всі значення у кілька інтервалів, кількість яких приймемо рівним п’яти. Для кожного інтервалу визначаємо відповідну частоту, а також відносну частоту – частість, яка показує як часто міцність трапляється у межах даного інтервалу.

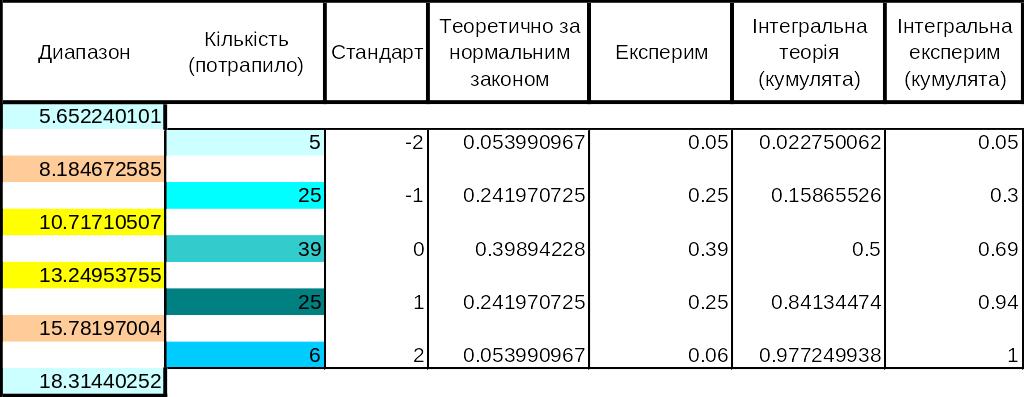
Далі наведемо гістограми розподілу випадкових величин міцності будівельного матеріалу, які є вибірковим аналогом кривої розподілу. Гістограми відносних частот – це ступінчаста фігура, яка складається з прямокутників, основами яких є часткові інтервали, а висоти дорівнюють щільності відносних частот. Площа окремого прямокутника дорівнює відносній частоті значень міцності, а площа всієї гістограми дорівнює сумі всіх відносних частот, тобто одиниці.

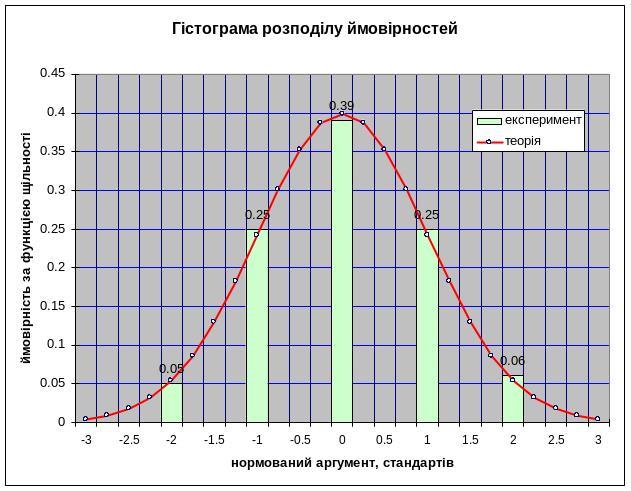
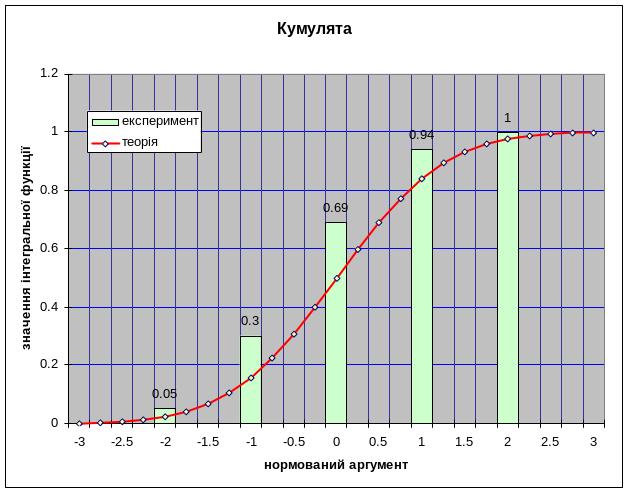
Як зазначено у публікаціях наукових досліджень міцності будівельних матеріалів, розподіл випадкових величин міцності підпорядкований статистичному закону нормального розподілу Гауса, ця гіпотеза буде нами перевірена у наступному п .1.3.

§1.3. Перевірка відповідності отриманого розподілу до закону нормального розподілу за критерієм Пірсона

Про передбачуваний закон розподілу випадкової величини можна судити по гістограмі, яку будують за даними варіаційного ряду. Однак точнішу оцінку відповідності вибіркового і теоретичного розподілів можна дати за допомогою спеціальних критеріїв. Ми скористаємось критерієм Пірсона. За цим критерієм встановимо приналежність нашого статистичного закону вибіркового розподілу до теоретичного розподілу Гауса. Статистику, за допомогою якої перевіряють гіпотези називають критерієм перевірки гіпотез. Параметри розподілу перевіряють за допомогою критеріїв значущості.

Головна вимога критерію перевірки гіпотези полягає у тому, щоб він не віжхиляв правильну гіпотезу, але з великим ступенем ймовірності відхиляв хибну. Під рівнем значуваності розуміємо ймовірність зробити помилку першого роду, для задачі нормування міцності рівень значущості приймають рівним 0.05, що означає 5% рівень значущості критерію перевірки гіпотези. Імовірність зробити помилку другого роду пов’язують із поняттям потужності критерію – ймовірності правильного відхилення хибної гіпотези. Емпіричне значення критерію Пірсона знаходять за формулою:

, де

К - кількість інтервалів,

n - об’єм вибірки,

- ймовірність того, що випадкова величина набуває значення, яке належить відповідному і-му інтервалу .

За табл. визначаємо теоретичне (критичне) значення критерію за заданим рівнем значущості критерію і кількістю ступенів вільності , при та :

.

Наведемо таблицю обчислення критерію Пірсона для наших даних:

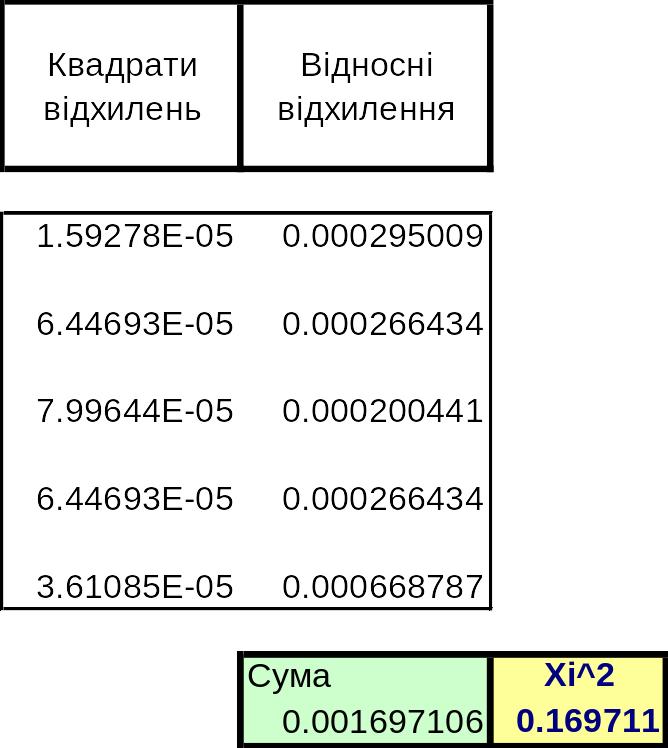
Завдяки тому, що 0,169711<6 тобто , приймається нормальний закон Гауса. За умовами індивідуального завдання статистичний ряд узгоджується із кривою Гаусса за критерієм ² -Пірсона. За умови такого закону розподілу міцності, всі подальші розрахунки нормативної міцності будуть виконуватись за відповідною функцією Лапласа.