4. Сдвиг. Кручение

4.13. Чистый сдвиг. Расчет на сдвиг (срез)

4.14. Крутящий момент. Деформации и напряжения

4.15. Расчет на прочность при кручении

4.15. Расчет на жесткость при кручении

4.13 Чистый сдвиг. Расчет на сдвиг (срез)

Такое напряженное состоя­ние, когда на гранях выделенного элемента возникают только касательные напряжения τ (рис. 4,1), называется чистым сдвигом.

Наиболее простой однородный чистый сдвиг может быть осуществлен непосредственным нагружением пластины, захваченной в жесткие контурные шарнирно соединенные накладки (рис. 4.2). Для всех точек пластины касательные напряжения τ будут, очевидно, следующими:

,

где δ – толщина пластины.

Исключение составляет узкая краевая зона, где пластина сопрягается с накладками. Здесь напряженное состояние будет отличным от чистого сдвига. Однако в соответствии с принципом Сен-Венана эти отклонения носят чисто местный характер, и область их распространения мала по сравнению с общими размерами напряженной пластины.

В качестве второго примера, иллюстрирующего состояние одно­родного чистого сдвига, можно рассмотреть тонкостенную цилиндрическую трубку, нагруженную моментами, при­ложенными в торцевых плоскостях (рис. 4.3). Здесь и далее внешний момент, в отличие от внутреннего, обозначается через М.

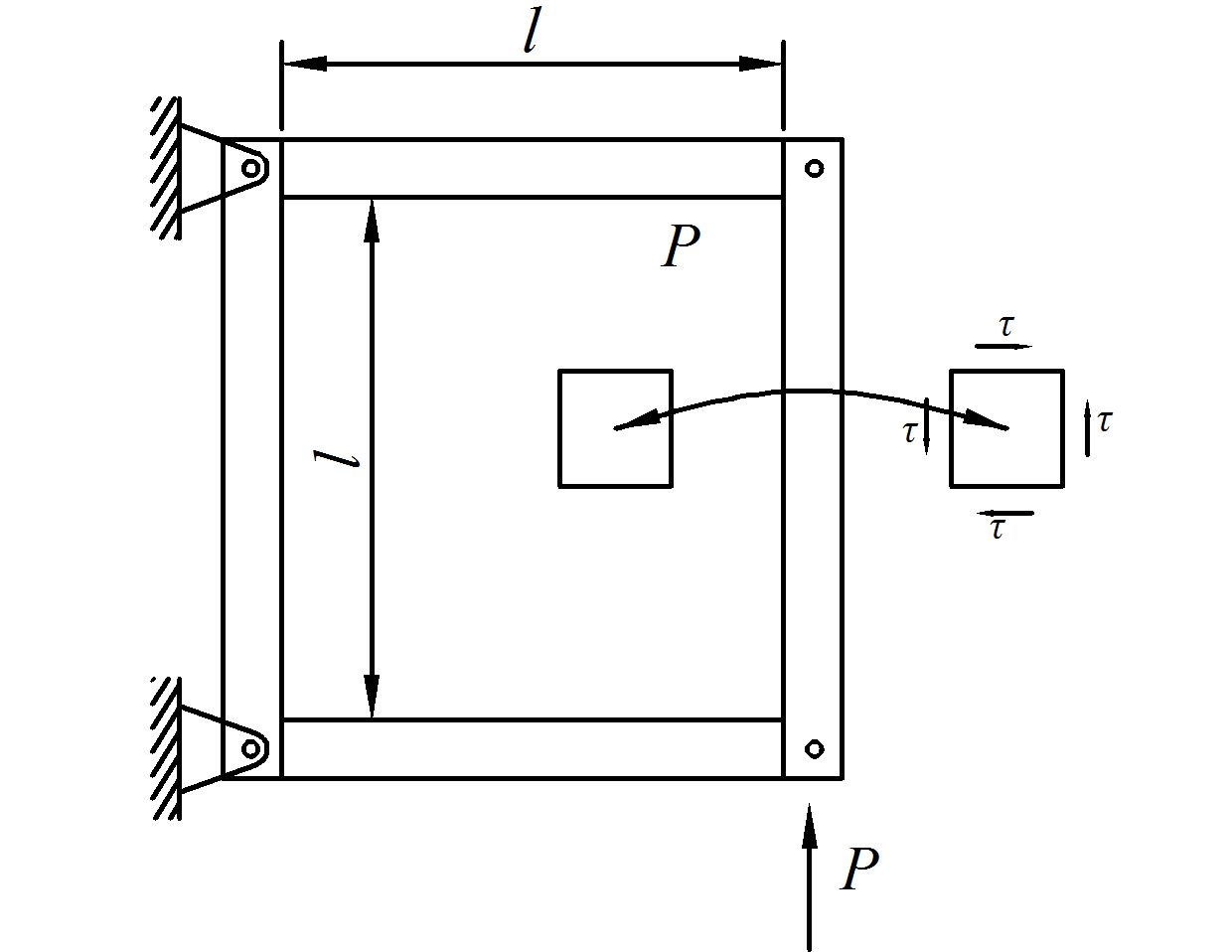
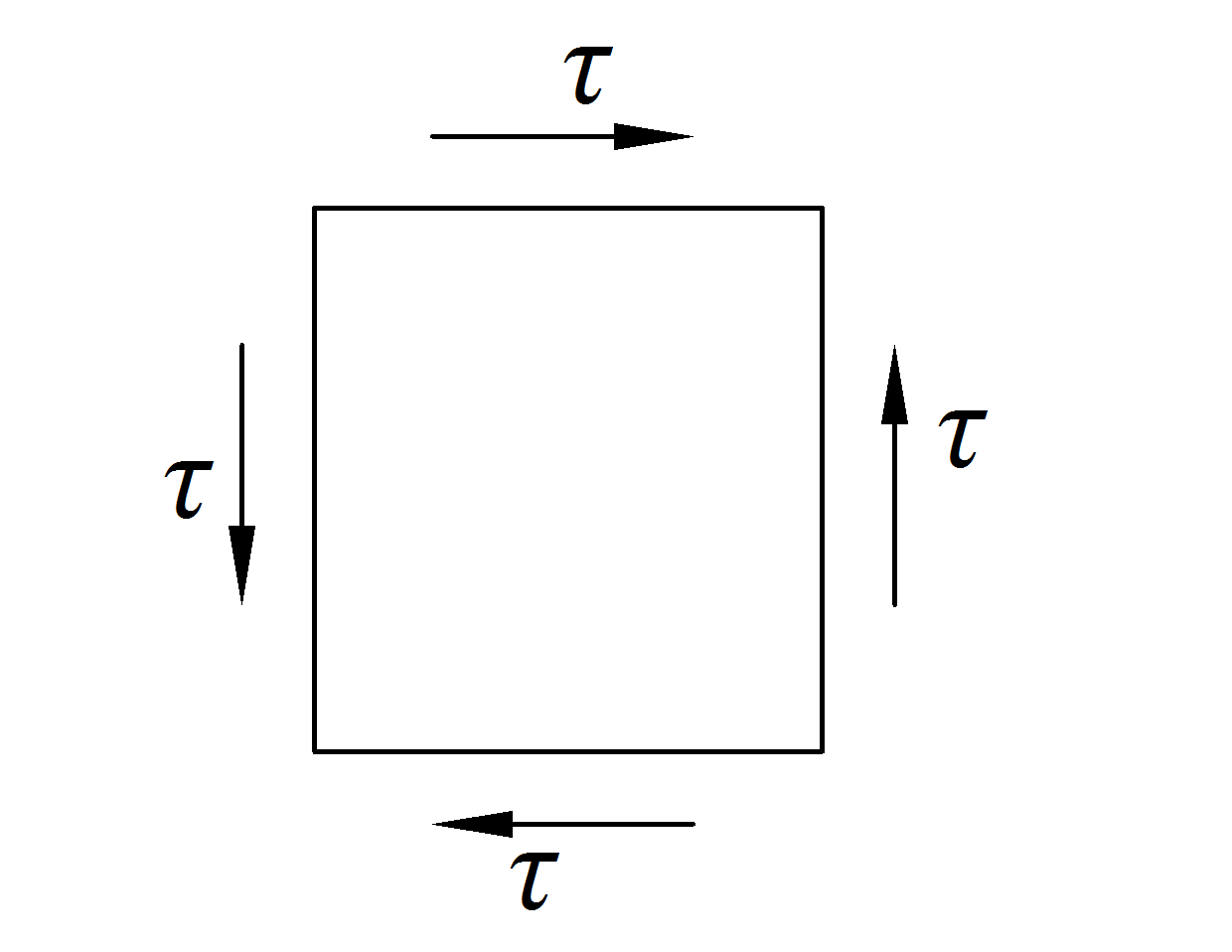
Рис. 4.1

Рис. 4.2

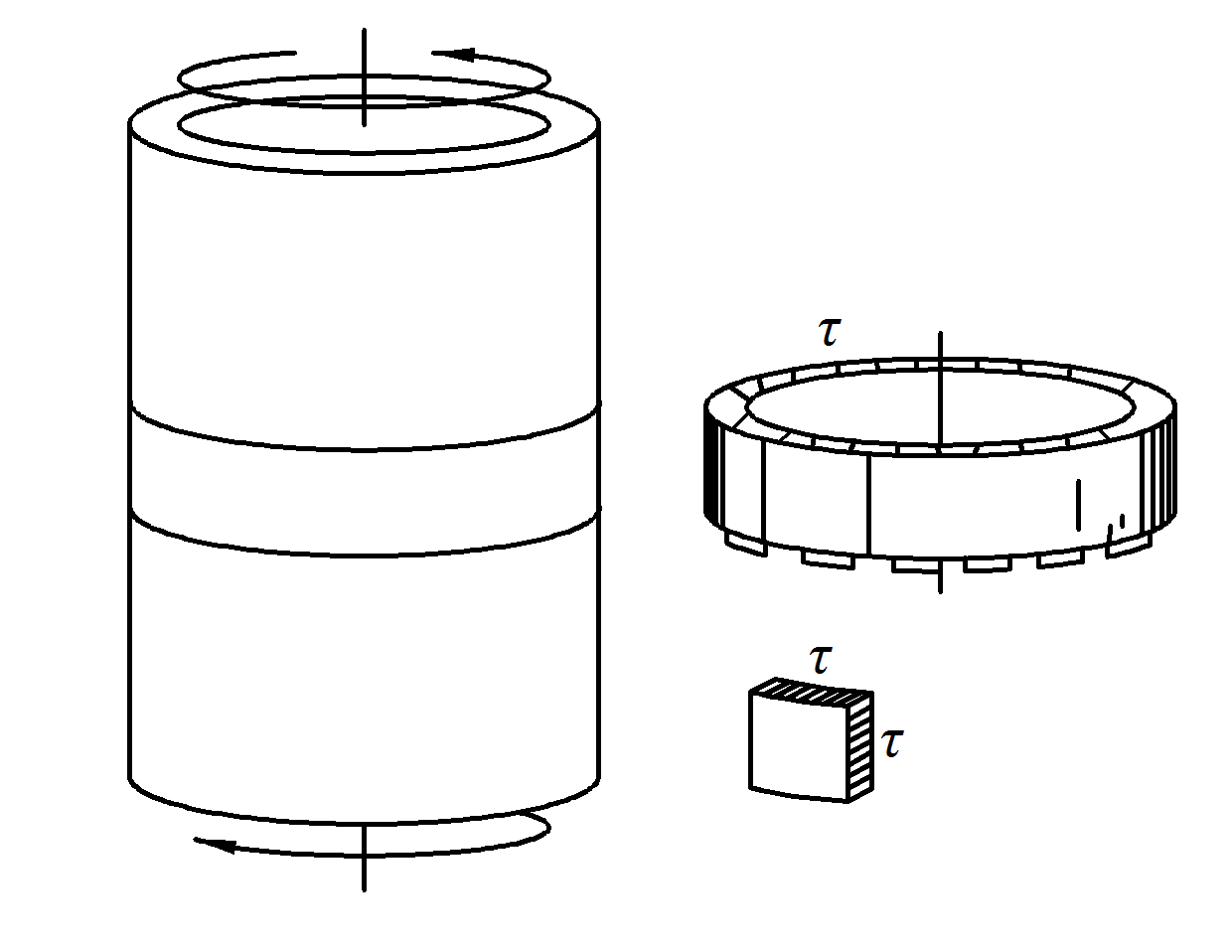
Рис. 4.3

Величина напряжения τ определяется из условий равенства момента равномерно распределенных по поперечному сечению внутренних сил моменту М:

,

где R – радиус трубки, а δ – ее толщина.

Рассмотрим деформации при сдвиге. Касательное напря­жение τ связано с угловой деформацией γ соотношением : τ=Gγ, где через G, как мы уже знаем, обозначена величина .

В результате возникающих угловых деформаций пла­стина, показанная на рис. 4.2, перекашивается, а торцевые сечения трубки (рис. 4.3) получают взаимные угловые сме­щения φ. Характер возникающих смещений показан на рис. 4.5, причем

.

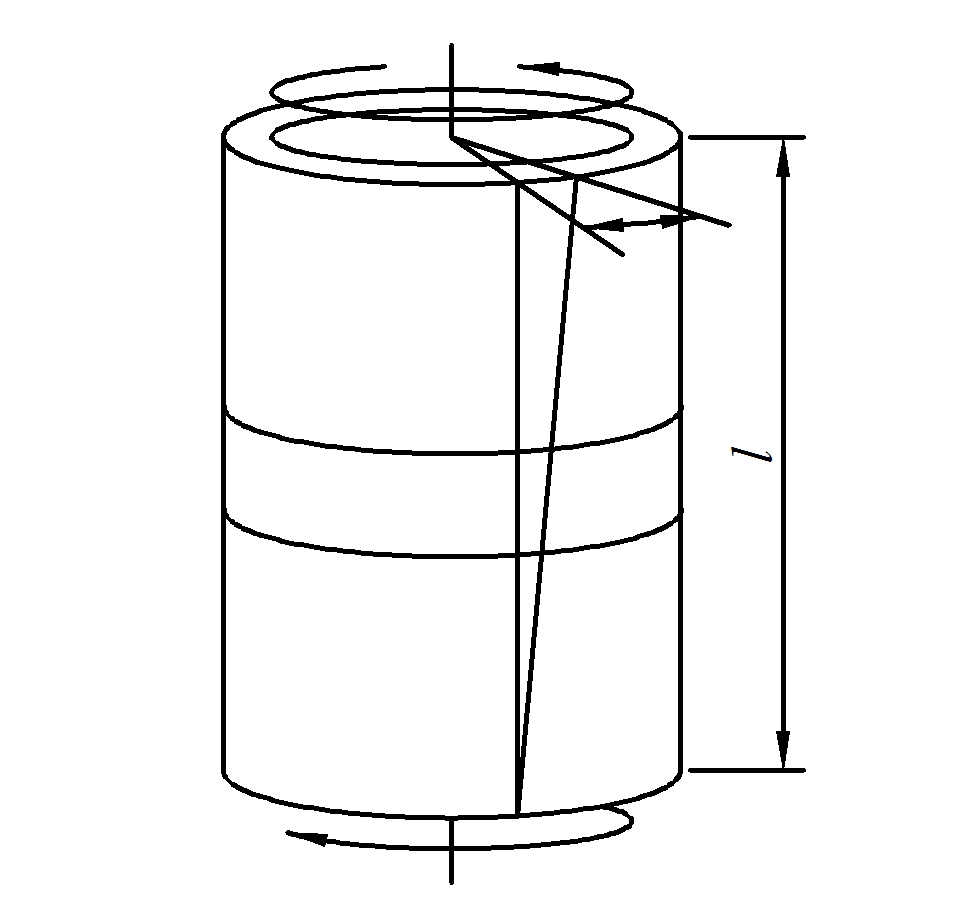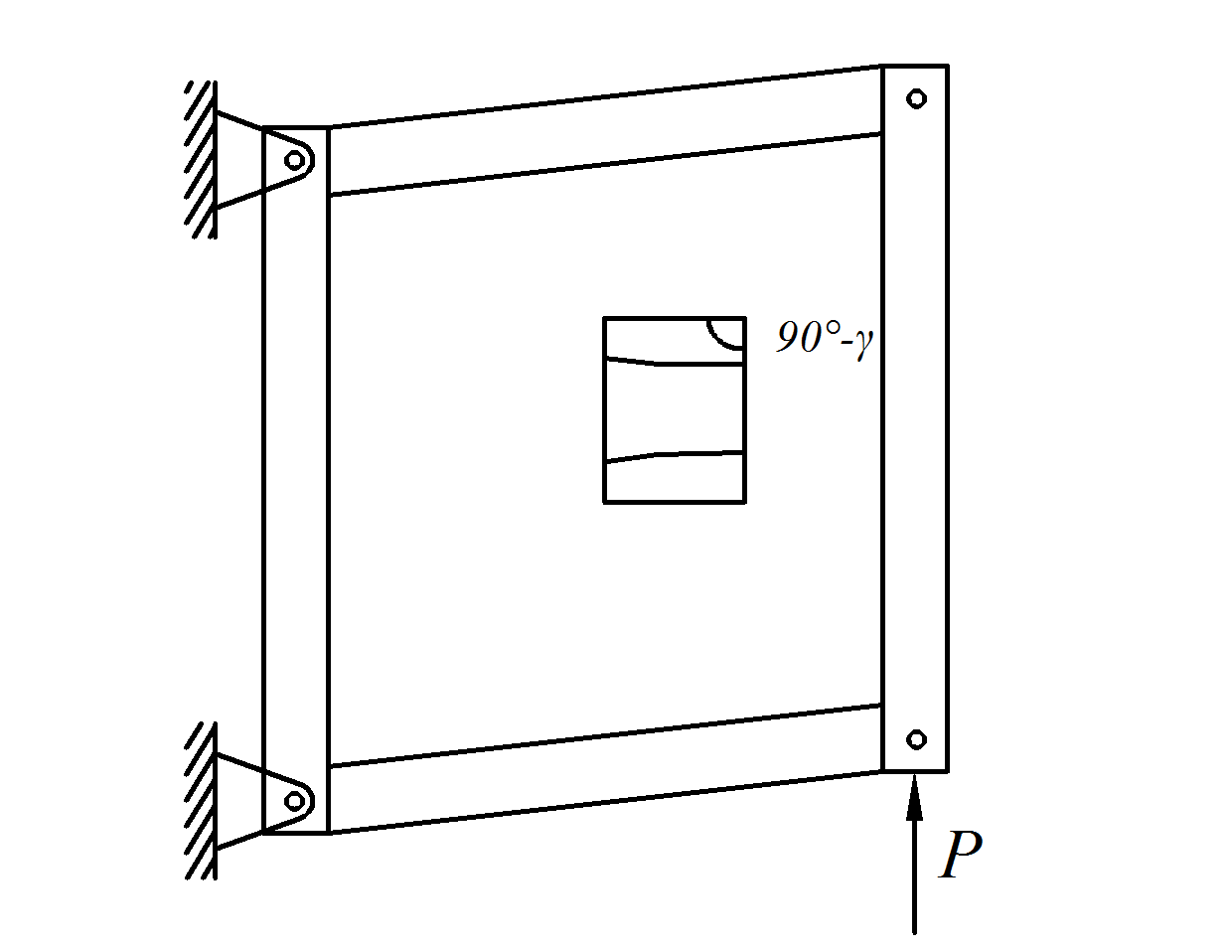
Рис. 4.5

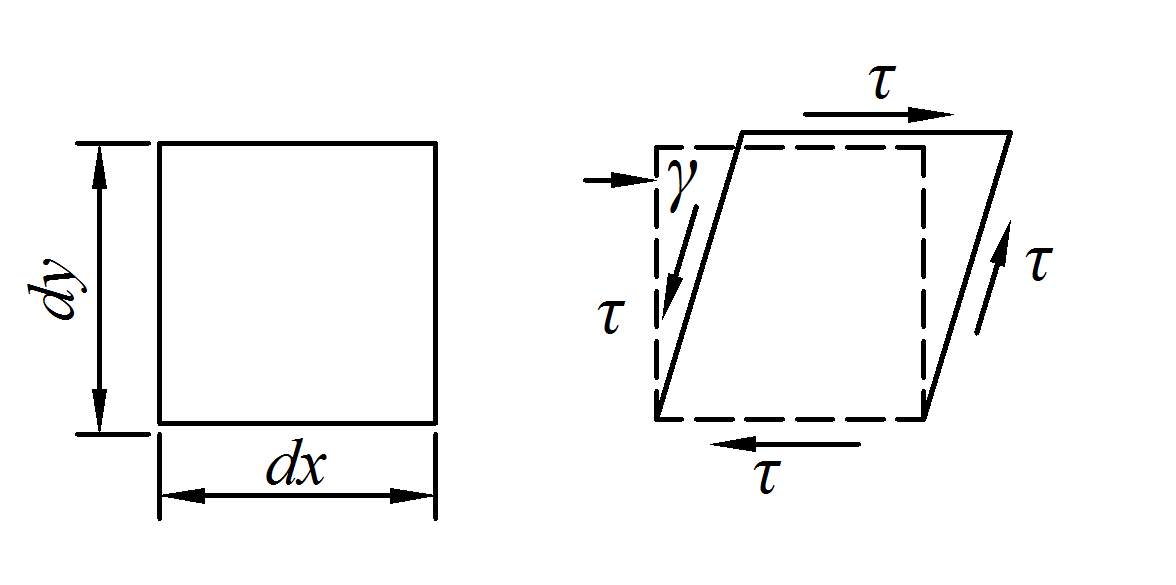
При чистом сдвиге, как и при растяжении (да и вообще при всяком напряженном состоянии), в деформируемом теле накапливается упругая потенциальная энергия. Эту энергию легко подсчитать, рассматривая изменение формы прямоугольного элемента с размерами dx, dy и толщиной δ (рис. 4.6).

Примем нижнюю грань элемента условно за неподвижную. Тогда при смещении верхней грани сила τdy. совершит работу на перемещении γdy. Так как сила меняется пропорционально смещению, то её работа равна половине произведения τdxδ·γdy. Следовательно, потенциальная энергия деформации, накопленная в элементе, равна dU=½τdxdyδ. Если отнести энергию к единице объема, получим

.

Выразим γ через τ по закону Гука. Тогда

.

Рис. 4.6

Величина U₀ называется удельной потенциальной энергией при сдвиге и измеряется в Дж/м².