Вариант №1
Контрольная работа №1
1. Решить систему уравнений тремя способами:
(а) по формулам Крамера;
(b) записать систему в матричной форме и решить ее матричным способом;
(с) методом Гаусса.
2. Даны четыре точки А(3;1;4), В(-1;6;1), С(-1;1;6), D(0;4;1).
(а) Составить уравнение прямой АВ и указать ее направляющий вектор.
(b) Составить уравнение плоскости, проходящей через точку D перпендикулярной прямой АВ.
(с) Составить уравнение плоскости АВС и указать ее нормальный вектор.
(d) Составить уравнение прямой, проходящей через точку D перпендикулярно плоскости АВС.
(e)
Определить, образуют ли векторы
базис.
(f) Найти угол между прямой АD и плоскостью АВС.
(g) Составить уравнение прямой BD и указать ее направляющий вектор.
(h) Составить уравнение плоскости α, проходящей через точки А, С параллельно прямой BD.
(i) Найти площадь треугольник АВС.
(j) Найти расстояние от точки В, до плоскости.
3.
Построить линию, определяемую уравнением
.
Контрольная работа №2
1. Вычислить пределы:
(а)
(с)
(b)
(d)
2. Найти производные первого и второго порядков функции:
(а)
(b)
(c)
3.
Составить уравнение касательной и
нормали к графику функции f(x)в
указанной точке
:
4. Провести полное исследование функции и построить график:
(а)
(b)
5. Найти наибольшее и наименьшее значение функции на данном отрезке:
6. Выполнить действия с комплексными числами. Результат представить в алгебраической и тригонометрической форме:
(а)
;
(b)
;
(с)
.
Вариант №2
Контрольная работа №1
1. Решить систему уравнений тремя способами:
(а) по формулам Крамера;
(b) записать систему в матричной форме и решить ее матричным способом;
(с) методом Гаусса.
2. Даны четыре точки А(3;1;2), В(-1;0;1), С(-1;1;3), D(0;-1;2).
(а) Составить уравнение прямой АВ и указать ее направляющий вектор.
(b) Составить уравнение плоскости, проходящей через точку D перпендикулярной прямой АВ.
(с) Составить уравнение плоскости АВС и указать ее нормальный вектор.
(d) Составить уравнение прямой, проходящей через точку D перпендикулярно плоскости АВС.
(e) Определить, образуют ли векторы базис.
(f) Найти угол между прямой АD и плоскостью АВС.
(g) Составить уравнение прямой BD и указать ее направляющий вектор.
(h) Составить уравнение плоскости α, проходящей через точки А, С параллельно прямой BD.
(i) Найти площадь треугольник АВС.
(j) Найти расстояние от точки В, до плоскости.
3.
Построить линию, определяемую уравнением
.
Контрольная работа №2
1. Вычислить пределы:
(а)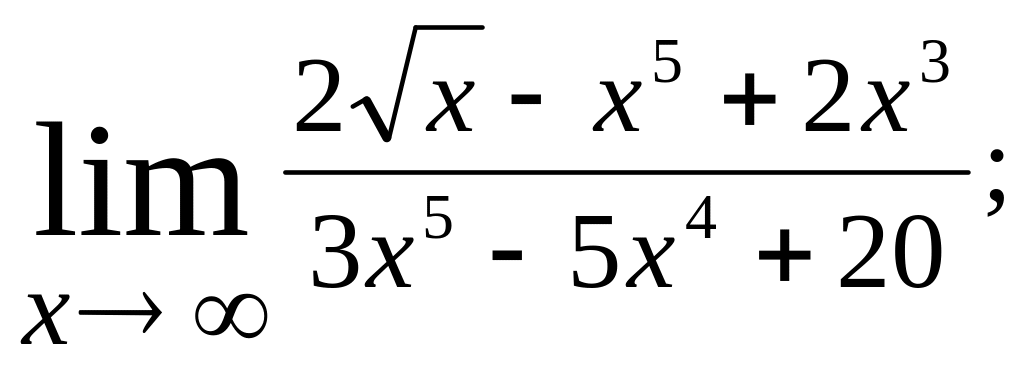
(с)
(b)
(d)
2. Найти производные первого и второго порядков функции:
(а)
(b)
(c)
3. Составить уравнение касательной и нормали к графику функции f(x)в указанной точке :
4. Провести полное исследование функции и построить график:
(а)
(b)
5. Найти наибольшее и наименьшее значение функции на данном отрезке:
6. Выполнить действия с комплексными числами. Результат представить в алгебраической и тригонометрической форме:
(а)
;
(b)
;
(с)
.
Вариант №3
Контрольная работа №1
1. Решить систему уравнений тремя способами:
(а) по формулам Крамера;
(b) записать систему в матричной форме и решить ее матричным способом;
(с) методом Гаусса.
2. Даны четыре точки а(-2;4;1), в(-1;1;0), с(3;-3;2), d(0;-1;2).
(а) Составить уравнение прямой АВ и указать ее направляющий вектор.
(b) Составить уравнение плоскости, проходящей через точку D перпендикулярной прямой АВ.
(с) Составить уравнение плоскости АВС и указать ее нормальный вектор.
(d) Составить уравнение прямой, проходящей через точку D перпендикулярно плоскости АВС.
(e) Определить, образуют ли векторы базис.
(f) Найти угол между прямой АD и плоскостью АВС.
(g) Составить уравнение прямой BD и указать ее направляющий вектор.
(h) Составить уравнение плоскости α, проходящей через точки А, С параллельно прямой BD.
(i) Найти площадь треугольник АВС.
(j) Найти расстояние от точки В, до плоскости.
3.
Построить линию, определяемую уравнением
.
Контрольная работа №2
1. Вычислить пределы:
(а)
(с)
(b)
(d)
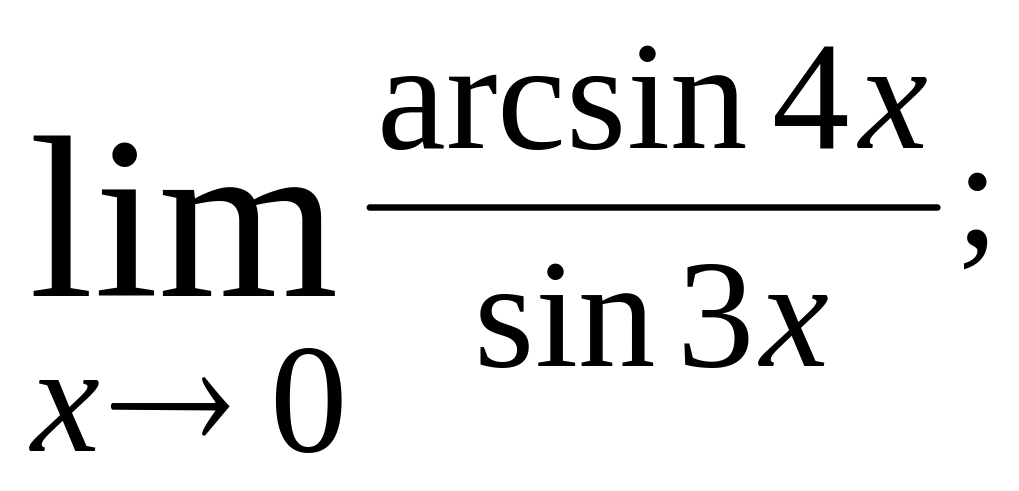
2. Найти производные первого и второго порядков функции:
(а)
(b)
(c)
3. Составить уравнение касательной и нормали к графику функции f(x)в указанной точке :
4. Провести полное исследование функции и построить график:
(а)
(b)
5. Найти наибольшее и наименьшее значение функции на данном отрезке:
6. Выполнить действия с комплексными числами. Результат представить в алгебраической и тригонометрической форме:
(а)
;
(b)
;
(с)
Вариант №4
Контрольная работа №1
1. Решить систему уравнений тремя способами:
(а) по формулам Крамера;
(b) записать систему в матричной форме и решить ее матричным способом;
(с) методом Гаусса.
