6. Релятивистская механика

Сложение скоростей в релятивистской механике

З начения и скорости точки в двух инерциальных системах отсчета К и К' равны

г де -радиус-векторы рассматриваемой точки в

с истемах отсчета К и К'. Проекции скоростей и на оси декартовых координат равны:

Если сходственные оси декартовых координат систем отсчета К я К' попарно параллельны и система К' движется относительно К с постоянной скоростью V, направленной вдоль оси ОХ, причем в момент начала отсчета времени в К и К' ( ) начала координат О и О' этих систем совпадают, то справедливы преобразования Лоренца. Из этих преобразований следует, что

где .

то связь междупроекциями скоростей точки на оси декартовых координат в систему отсчета К и К' имеет вид

Эти формулы выражают закон сложения (преобразования) скоростей в релятивисткой кинематике. В пределе при они приводят к обычному закону сложений скоростей в классической механике Ньютона:

Парадокс близнецов

Парадокс близнецов — мысленный эксперимент с двумя близнецами N и N` движущимися относительно друг друга. Согласно эффекту релятивистского замедления времени каждый из близнецов считает (и это подтверждается его наблюдениями), что часы другого близнеца идут медленнее, чем его часы.

Если один из близнецов улетит, а потом вернётся, то кто из них окажется младше?

Младше окажется улетавший и вернувшийся.

Возникает парадокс: почему, если каждый видел, что время замедляется у другого, младше становится именно улетавший?

Объяснение на примере обмена сигналами. Пусть один близнец (назовём его космонавтом) полетел к Альфе Центавра со скоростью скорости света, и они с братом договорились каждый месяц посылать друг другу контрольные сообщения. Посчитаем, когда землянин получит 12-й сигнал от космонавта. То есть расчеты, сейчас будем вести по часам землянина. Поскольку время у космонавта при такой скорости замедляется в раза, то 12-й сигнал космонавт пошлёт через месяцев. За это время он улетит на световых месяцев. В итоге 12-й сигнал будет получен землянином через 20+16=36 месяцев. Таким образом, видим, что сигналы приходят в раза реже, чем было уговорено.

Аналогичный расчёт показывает, что когда космонавт будет возвращаться, то сигналы будут приходить в 3 раза чаще, чем было уговорено: . Поскольку инерциальные системы равноправны, то проведя аналогичные

расчёты, но уже с точки зрения космонавта, мы получим аналогичную картину: космонавт тоже будет видеть, что часы землянина идут медленнее, и точно так же будет, удаляясь, получать от землянина сигналы в три раза реже, а приближаясь — в три раза чаще, чем было уговорено. И это естественно, инерциальные системы равноправны. Теперь посмотрим, какую часть времени каждый близнец будет получать частые сигналы, а какую — редкие. Сигнал о том, что космонавт развернулся и летит назад, землянин получит не сразу, а когда космонавт уже пролетит расстояния назад. Если пренебречь временем на разворот (пусть космонавт разворачивается мгновенно), то времени землянин получал редкие сигналы, а — частые. Космонавт же частые сигналы начал получать сразу же после разворота. То есть времени он получал редкие, а — частые сигналы. В данном случае проявляется неравноправие систем отсчёта. В итоге по земным часам до Альфы Центавра (4 световых года) космонавт летел лет туда и столько же обратно. За эти 10 лет девять лет приходили редкие сигналы, а 1 год — частые. Общее число сигналов . Разделим на 12 и получим 6 лет, которые прошли у космонавта. Для космонавта расстояние до Альфы Центавра сократилось в силу релятивистского сокращения расстояний и составило световых лет. До неё со своей скоростью он долетел за 3 года. Ну и столько же на полёт обратно. За это время он получил сигналов от землянина. То есть по наблюдениям космонавта на земле прошло 10 лет. Как видим, и по наблюдениям космонавта, и по наблюдениям землянина на Земле проходит 10 лет, а на борту — 6.

Данное объяснение не исходит из того, что время замедляется только у космонавта, а основано на принципе равноправности инерциальных систем. Неравноправие возникает только из-за разворота космонавта, так как при развороте его система перестаёт быть инерциальной.

Релятивистская динамика

Преобразование импульса и энергии

В релятивистской динамике, так же как и в классической механике, импульс тела определяется как произведение массы на скорость. Но из условия, что фундаментальный закон сохранения импульса должен исполняться в любой инерциальной системе отсчета, выплывает, что (в отличии от классической механики) масса частицы зависит от ее скорости: (1)

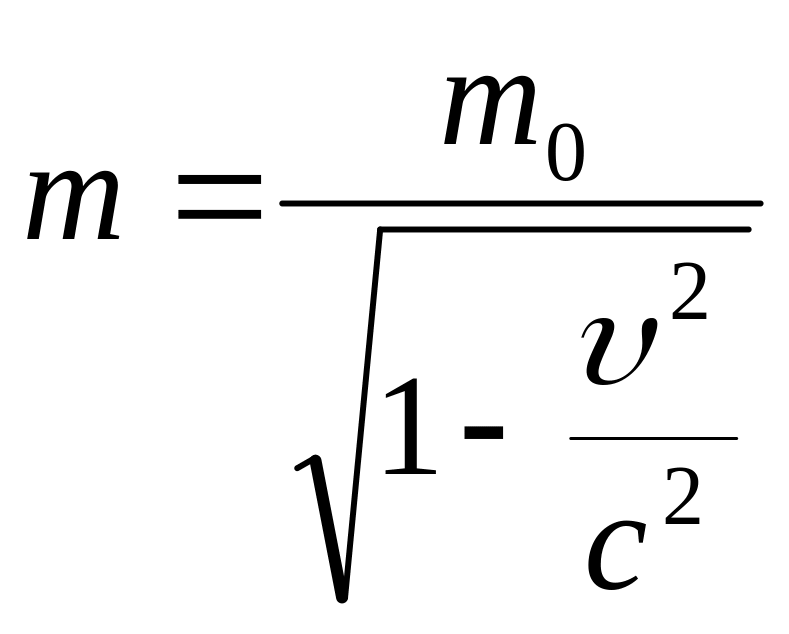
Где m₀ – масса покоя; - скорость частицы в системе К.

Масса частицы m называют релятивистской массой. В отличии от этой массы , масса покоя m₀ – величина инвариантная , т.е. одинаковая во всех инерциальных системах отсчета . Именно поэтому массу m₀ принимают как характеристику частицы.

Учитывая предыдущее уравнение, импульс частицы в релятивистской динамике имеет вид: (2)

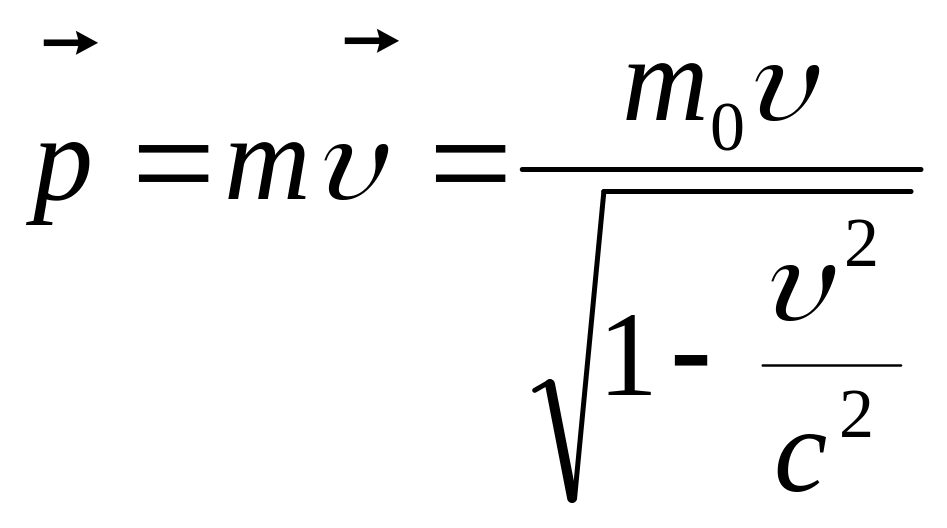
При <<с уравнение превращается в ньютоновское определение импульса , где m₀ не зависит от скорости (в классической механике m= m₀)

Основное уравнение релятивистской динамики.

Согласно принципа относительности Эйнштейна все законы природы должны быть инвариантными относительно инерциальных систем отсчета. Другими словами, математическая запись законов должна иметь один и тот же вид во всех этих системах. Оказывается, что в общем случае основное уравнение динамики Ньютона не соответствует этому принципу. Вместе с этим в теории относительности доказано, что этому соответствует уравнение: (3)

Где - сила, которая действует на частицу. Приведенное уравнение полностью совпадает видом с основным уравнением ньютоновской динамики, но его физическое содержание отлично.

В этом уравнении слева стоит производная не от классического, а от релятивистского импульса. Совместим последние два уравнения и получим: (4)

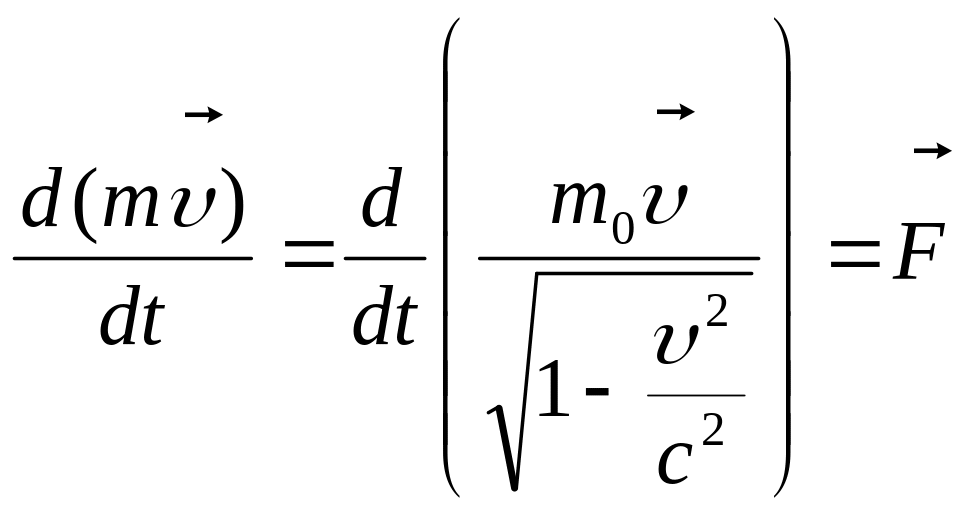
Это уравнение и есть основным уравнением релятивистской динамики. Очевидно, что именно в этом виде уравнение вызывает сохранение импульса для свободной частицы ( =0) и при <<с принимает форму основного уравнения ньютоновской динамики ( , где m=m₀)

Из основного уравнения релятивистской динамики следует: вектор ускорения частицы в общем случае не совпадает с направлением вектора силы . Действительно: (5)

Где m – релятивистская масса.

После дифференцирования этого выражения по времени получаем: (6)

Это выражение графически изображается на рис.12 , где мы видим, что вектор ускорения не коллинеарен вектору .

З аметим, что вектор ускорения сбегается с вектором силы только в двух случаях: вектор силы перпендикулярный вектору скорости (поперечная сила); вектор силы параллельный вектору скорости (продольная сила). Поскольку в первом случае сила, которая

Рис.12действует на частицу,- продольная, она изменяет только направление скорости и не

Рис.12 изменяет саму ее величину, . При этом условии производная в предыдущем выражении равна нулю (релятивистская масса зависит от скорости, но в данном случае , следовательно ), и уравнение приобретает вид: (7)

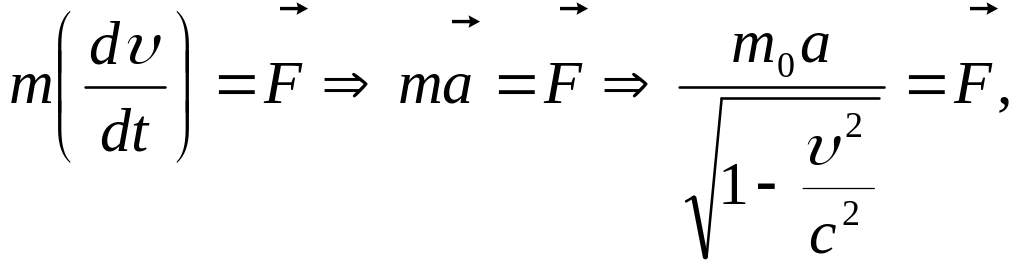
или

Векторы и совпадают по направлению.

Для случая продольной силы ( параллельно ) уравнение (7) имеем право просто переписать в скалярном виде. Взяв производные в левой части этого уравнения, получим: (8)

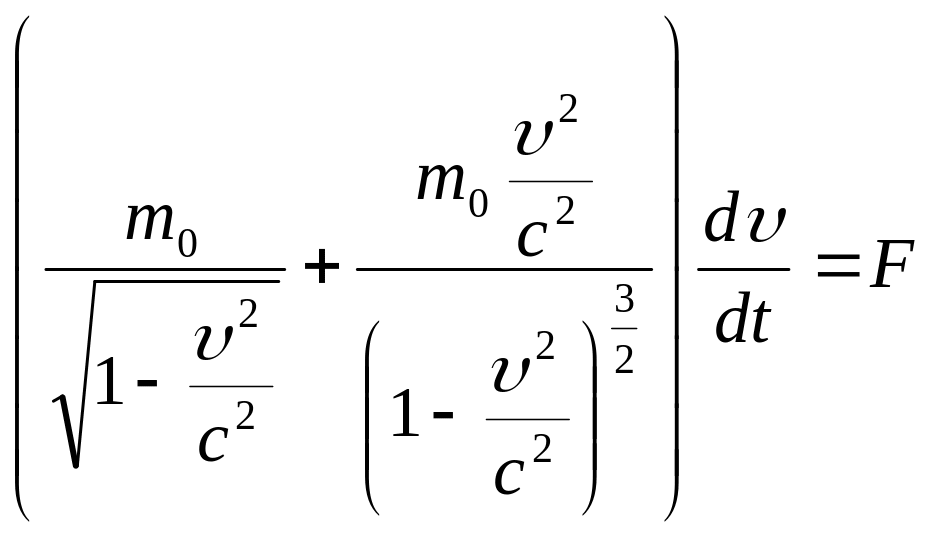
откуда: (9)

или в векторном виде

С этих выражений следует, что при одинаковых в обоих случаях значениях силы и скорости поперечная сила придает частице большее ускорение, чем продольная.

Кинетическая энергия релятивистской частицы

Определим кинетическую энергию так же как и в классической механике, а именно как величину, прирост которой равен работе силы, которая действует на частицу: (10)

В соответствии с уравнением (3)

где m- релятивистская масса

Итак, принимая во внимание, что

, а ,

где - проекция вектора на направление вектора , имеем (11)

Возведем формулу(1) в квадрат и приведем ее к виду: (12)

Теперь найдем дифференциал этого выражения, имея в виду, что m₀ и с - постоянные величины(13)

Разделив предыдущее выражение на 2m, получим (14)

Правая часть выражения совпадает с правой частью выражения для кинетической энергии (11), то есть: (15)

Таким образом, прирост кинетической энергии частицы пропорционален приросту ее релятивистской массы. Кинетическая энергия неподвижной частицы равна нулю, а ее масса равна m₀. Итак, проинтегрировав полученное выражение, получим (16)

или (16)

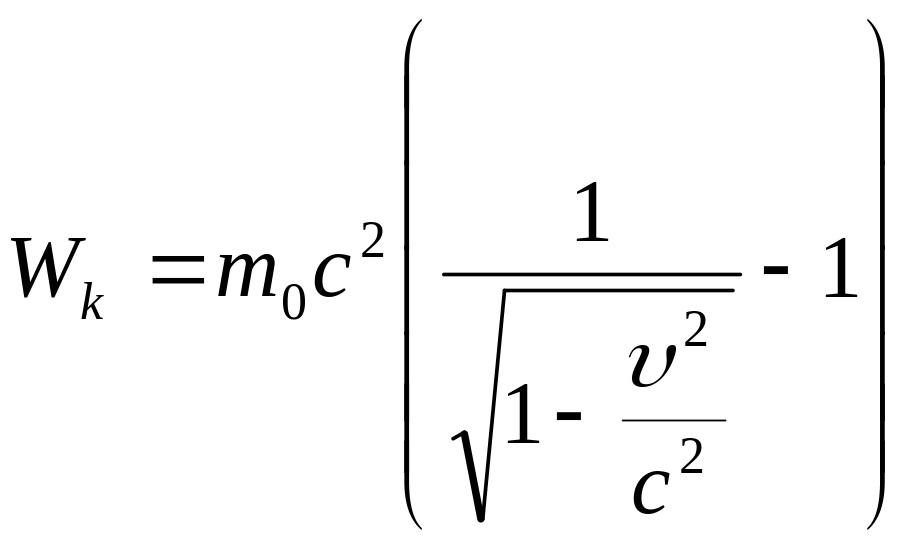
Это и есть выражение для релятивистской кинетической энергии. Если <<с мы должны получить выражение для классической кинетической энергии . Воспользуемся формулой бинома Ньютона, согласно которой

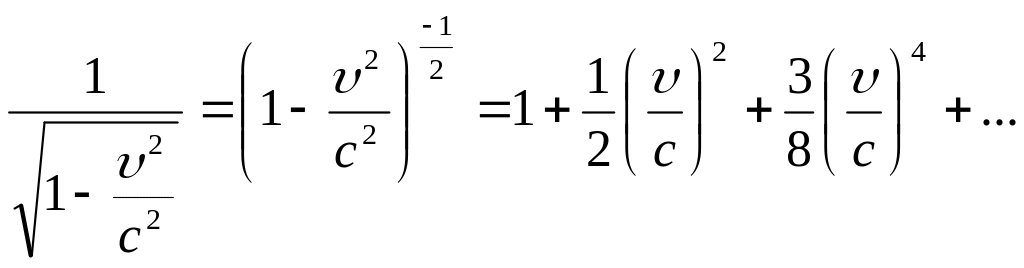
При условии <<с можно ограничиться только двумя членами ряда, и тогда выражение (16) превратится в (17)

Таким образом, при <<с выражение для релятивистской кинетической энергии преобразуется в классическое выражение для кинетической энергии. Отметим, что аналогично классической механике релятивистскую кинетическую энергию нельзя представить в виде , где m – релятивистская масса частицы.

Частица с нулевой массой покоя

Фотоны- наименьшие частицы света. Их также называют квантами света. Корпускулярные (квантовые) свойства света проявляются, например, в явлениях фотоэффекта или при исследовании давления света. Фотон, так же как и любая другая материальная частица, имеет массу, импульс и энергию.

И все-таки фотон отличается от других частиц тем, что всегда движется с постоянной скоростью, которую нельзя изменить. Скорость фотона равна скорости света и одинакова во всех инерциальных системах отсчета.

Но тогда образуются определенные осложнения с массой. При релятивистская масса стремится к бесконечности в соответствии с формулой:

Но этого не может быть. Можно предположить, что масса покоя равна нулю.

Эксперимент подтверждает, что масса покоя фотона во много раз меньше массы электрона. Вывод: частица с нулевой массой покоя всегда движется со скоростью света.

Но масса движения, т.е. инертная масса, фотону присуща.

Для начала определим другие характеристики фотона: энергию и импульс.

Энергия фотона, как известно, зависит от частоты электромагнитной волны :

где h=6,63^.10^-34Дж^.с – постоянная Планка.

Импульс фотона найдем, воспользовавшись связью энергии и импульса.

Поскольку m₀=0, тогда импульс фотона равен:

А теперь можно найти и массу фотона, поскольку его импульс равен: p=mc. Масса фотона:

Список литературы:

1. Бовтук А.Г, Герасименко Ю.Т, Лахин Б.Ф та ін. Фізика. Модуль 1. Механіка: Навч. Посібник (за заг. ред. проф. А. Поліщука. – К.: Книжкове вид-во НАУ, 2008. – 176 с.

2. Детлаф А.А, Яворский Б.М Курс физики. - К.: Высшая школа, 1999.-688 с.

3. Малов Б.А Физические основы механики: Учебное пособие. – К.: КНИГА, 1993. – 68 с.

4. Соловйов А.М. Лекції професора Соловйова з фізики. Фізичні основі механіки. – К.: КМУЦА, 1999.- 92 с.

ович

Київ 2014

Министерство науки и образования Украины

Национальный авиационный университет

Факультет телекоммуникаций

Реферат по физике на тему: