Вывод уравнения движения в форме Рейнольдса Уравнение движения вязкой жидкости в форме Навье-Стокса
Для вывода уравнения Навье-Стокса воспользуемся уравнениями движения в проекциях на оси координат, выраженными через напряжения
,
,
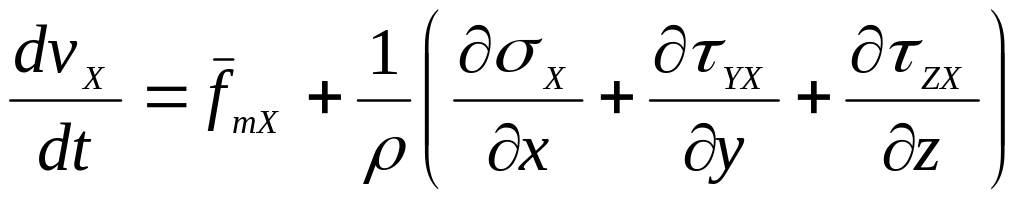(7.3)
и выражениями для касательных и нормальных напряжений (обобщенным законом Ньютона для сплошной вязкой среды)
,
,
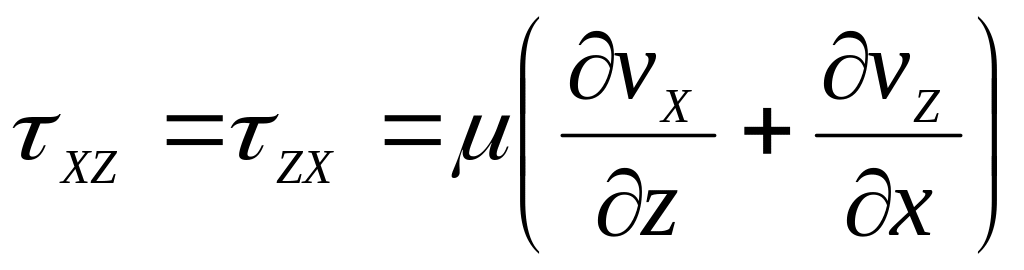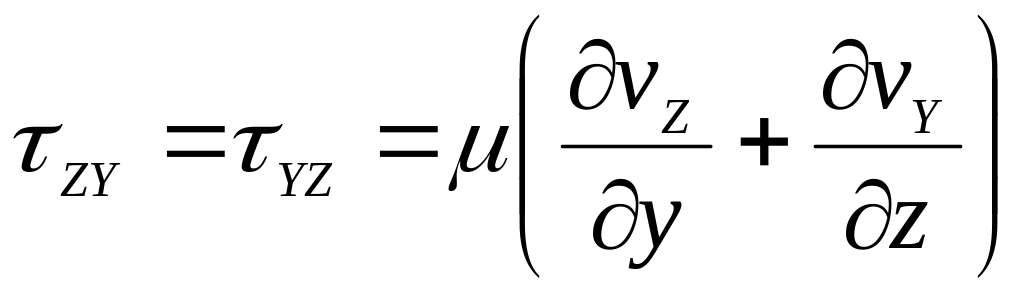(7.4)
,
,
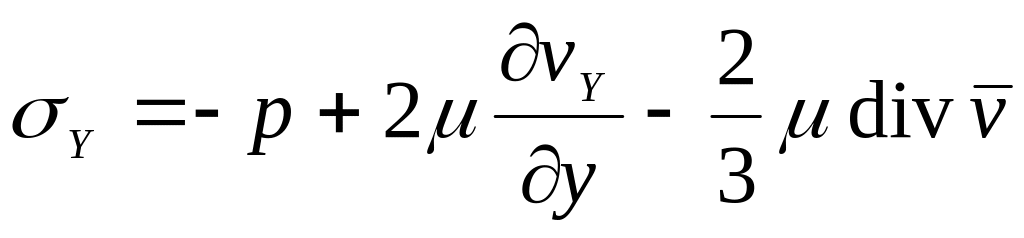(7.5)
Подставляя соответствующие выражения из (7.4) и (7.5) в проекцию выражения (7.3) на ось x и считая =const, получаем
.
Собирая члены со вторыми производными vx по координатам и с производными по х от divŪ, получаем
, (7.6)
где
- оператор Лапласа.
Выполнив аналогичные преобразования с проекциями на оси y и z получаем
(7.7)
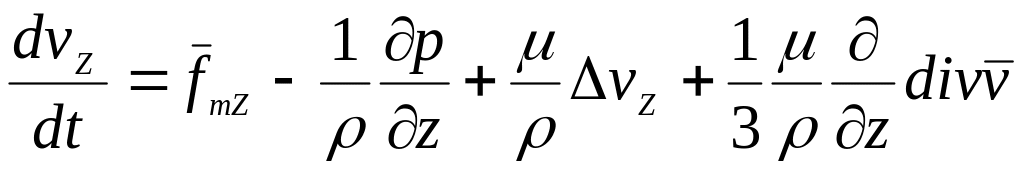. (7.8)
В векторной форме уравнение Навье - Стокса принимает вид
. (7.9)
Для несжимаемой жидкости divŪ =0 и уравнение Навье - Стокса имеет вид
. (7.10)
Подчеркнем, что в уравнение Навье — Стокса входят истинные значения скоростей и давлений и их производные.
Уравнение движения в форме Рейнольдса
Полученные выше уравнения Навье-Стокса для движения вязкой жидкости не удобны при исследовании турбулентного течения вязкой жидкости, так как содержат фактические значения скорости и давления, а не осредненные.
Если в уравнении Навье - Стокса для несжимаемой вязкой жидкости скорости и давления заменить средними и пульсационными значениями, а затем произвести осреднение по времени, то получим уравнения Рейнольдса (1895 г.).
Произведя интегрирование по времени с одновременным делением на промежутки интегрирования, получим следующее выражение в направлении оси х:
На каждом участке интегрирования
,
но так как в данном случае выполняется
осреднение для n
участков, то
.
Так как по свойству осреднении произведения
и
,
то второе слагаемое левой части уравнения
будет иметь вид
.
Аналогично можно поступить с третьим и четвертым членами левой части уравнения. Окончательно в направлении оси x будем иметь:
,
Преобразуем последнюю скобку. Т.к.
,
то получим
Собрав все приведенное выше вместе получим для оси x, y и z: (7.11)-(7.13)
Тензор рейнольдсовых напряжений
Уравнения (7.11)-(7.13) называются уравнениями
Рейнольдса для турбулентного движения
несжимаемой жидкости, а величины
называют рейнольдсовыми напряжениями,
образующими тензор содержащий нормальные
и касательные напряжения Рейнольдса:
. (7.14)
Уравнения Рейнольдса отличаются от уравнений Навье - Стокса наличием девяти (точнее говоря, шести) дополнительны членов, учитывающих пульсации скорости. Наличие пульсационных скоростей в турбулентном потоке приводит к образовании как бы дополнительных напряжений, которые имелись бы в ламинарном потоке, если бы распределение скоростей в нем совпадало с распределением осредненных скоростей в турбулентном потоке.
Если вернуться к выводу уравнения Навье
- Стокса из уравнения для несжимаемой
жидкости (
),
записанного через напряжения (7.3) и
сопоставить их с полученными выше
уравнениями Рейнольдса, то увидим, что
полные нормальные и касательные
напряжения выражаются в виде алгебраической
суммы обычных напряжений в осреднением
потоке вязкой жидкости (см. формулы
(7.5) при
и (7.4)) и напряжений Рейнольдса
в виде
,
и т.д. (7.15)
В большинстве случаев в ядре потока турбулентные напряжения больше ламинарных, поэтому ламинарные составляющие часто можно не учитывать. Граничные условия с физической точки зрения остаются теми же, что и при ламинарном режиме течения (условия прилипания), т.е. на стенке обращаются в нуль все составляющие скорости, в том числе и пульсационные. На стенке остаются только нормальные и касательные напряжения ламинарного течения. У самой стенки образуется так называемый ламинарный подслой, в котором силы вязкости значительно превышают силы инерции. Следует подчеркнуть, что для расчета параметров осредненного течения необходимо знать связь между пульсационными скоростями и скоростями осредненного движения, что являются основной проблемой замыкания уравнений Рейнольдса.