7. Особенности моделирования турбулентных течений (4 часа).

Лекция 16. Уравнение энергии в дифференциальной и интегральной форме. Турбулентное движение и осреднение его параметров. Вывод уравнения движения в форме Рейнольдса. Тензор рейнольдсовых напряжений. Физические основы турбулентности. Гипотеза Буссинеска и длина пути смешения Прандтля Выбор модели турбулентности. Строение турбулентного пограничного слоя. Профиль скорости в пограничном слое. Логарифмический и степенной профиль скорости.

Лекция 17. Алгебраические модели турбулентности. Однопараметрические модели турбулентности. Уравнение кинетической энергии турбулентности. Диссипация энергии турбулентности. Основные допущения двухпараметрических моделей турбулентности. Семейство двухпараметрических диссипативных k- моделей турбулентности. Стандартная k- модель. Модель переноса касательных напряжений "SST" k-. Модели более высокого уровня.

7. Особенности моделирования турбулентных течений (4 часа). 0

Уравнение энергии в дифференциальной и интегральной форме 1

Турбулентное движение и осреднение его параметров 2

Основные понятия 2

Правила осреднения 3

Вывод уравнения движения в форме Рейнольдса 4

Уравнение движения вязкой жидкости в форме Навье-Стокса 4

Уравнение движения в форме Рейнольдса 5

Тензор рейнольдсовых напряжений 6

Турбулентность 6

Физические основы турбулентности 6

Гипотеза Буссинеска 8

Длина пути смешения Прандтля 9

Турбулентный пограничный слой 10

Строение турбулентного пограничного слоя 10

Профиль скорости в пограничном слое. Логарифмический профиль 11

Степенной профиль скорости в пограничном слое 12

Алгебраические МТ 13

Свободно-турбулентные течения 13

Пристеночные течения 14

Однопараметрические МТ 14

Уравнение кинетической энергии турбулентности 15

Диссипация энергии турбулентности 16

Двухпараметрические МТ 17

Основные допущения двухпараметрических МТ 17

Стандартная k- модель турбулентности 17

RNG k- модель турбулентности 18

Стандартная k- модель турбулентности 19

Модель переноса касательных напряжений SST k- 19

Модели более высокого уровня 20

МТ с неизотропной турбулентной вязкостью 20

Модель Рейнольдсовых напряжений RSM 20

МТ с набором фильтрующих уравнений 20

Сравнение RANS и LES 21

Пример 1. Течение в U-образном колене 22

Пример 2. Теплообмен при обтекании тупоконечной пластины 24

Пример 3. Теплообмен при обтекании лопатки СА 25

Уравнение энергии в дифференциальной и интегральной форме

В дополнение к уравнению неразрывности и уравнениям движения, связывающим параметры потока и их производные по координатам и по времени, необходимо получить уравнение сохранения энергии для этого потока. Для этого рассматривается некоторая масса жидкости, которую можно было бы "стянуть" в точку в связи с непрерывностью изменения параметров потока.

Закон сохранения энергии этой системы заключается в том, что приращение полной энергии Э массы жидкости за единицу времени равно работе L, совершенной внешними силами, и притоку теплоты Q за то же время:

,

причем положительными считаются подведенная работа и подведенная теплота. Под полной энергией единицы массы здесь понимается сумма ее внутренней энергии =C_VT и кинетической энергии v²/2.

В интегральной форме уравнение сохранения энергии для выделенного объема V и поверхности S принимает вид

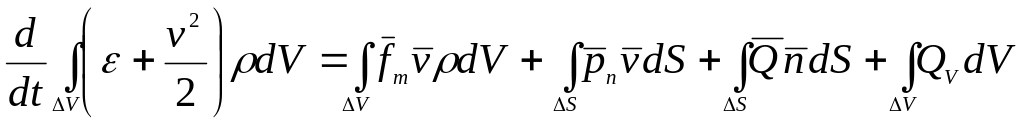(7.1)

Первый и второй члены правой части уравнения (7.1) определяют работу внешних сил - массовых и поверхностных , а третий и четвертый члены - подведенную теплоту, причем теплота состоит из теплоты от теплопроводности, конвекции и излучения, а теплота , включает в себя теплоту химических реакций, диссоциации и ионизации. Теплота джоулева нагрева в случае движения проводящей среды в электромагнитном поле связана с работой пондеромоторных сил, входящих в первый член правой части уравнения (7.1).

Для перехода к дифференциальной форме записи уравнения сохранения энергии с учетом того, что dV=dm=const для данного объема, преобразуем:

.

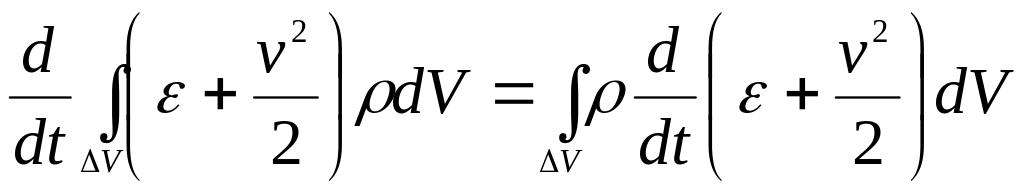Третий член правой части уравнения (7.1) преобразуется по формуле Остроградского - Гаусса:

Работу поверхностных сил (второй член правой части уравнения (7.1)) подсчитываем для параллелепипеда объемом V=xyz (общность полученных при этом результатов не нарушится, т.к. объем затем "стягивается" в точку). Преобразуем второй член правой части уравнения (7.1) к виду

При вычислении каждого из интегралов учитываем, что косинус угла между п и осью координат равен нулю для всех граней параллелепипеда, кроме двух граней перпендикулярных к данной оси.

Следовательно, разлагая в ряд Тейлора произведение и считая его постоянным для грани, получаем , откуда следует, что , где производные типа вычисляются в одной точке объема V и остаются постоянными для всего объема V.

Интегрируя все члены (7.1) по объему V и сокращая результат на V, получаем уравнение сохранения энергии в дифференциальной форме:

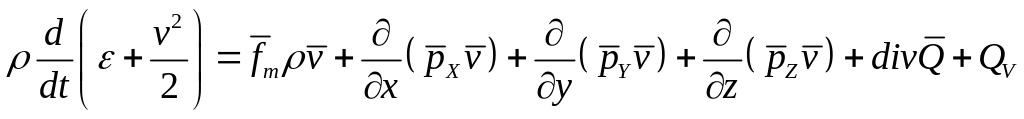, (7.2)

справедливой для произвольной точки потока.