Министерство образования и науки РФ

ФГБОУ ВПО

«Восточно-Сибирская государственная академия образования»

Кафедра технологий, предпринимательства и методик их преподавания

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению самостоятельных заданий

по начертательной геометрии

для студентов направления профессиональное обучение (транспорт)

очной формы обучения

Иркутск 2012

Автор-составитель

ст. преподаватель кафедры ТПиМП

Н.В. Трухина

ВВЕДЕНИЕ

Начертательная геометрия изучает методы точного изображения пространственных форм на плоскости, графические способы решения задач и геометрические свойства фигур.

Изучение начертательной геометрии развивает общее научное мышление человека, совершенствует его пространственное представление.

Все задачи начертательной геометрии решаются в пространстве. Способность пространственного представления приобретается не сразу, а вырабатывается в процессе основательного изучения теоретического материала и самостоятельного решения задач.

Самостоятельные задания выполняются на листах чертежной бумаги формата А3 (297х420). Внутри формата вычерчивается рамка, удаленная от левой кромки листа на 20мм, а от остальных кромок - на 5мм. В правом нижнем углу формата вплотную к рамке выполняется основная надпись, форма, размеры и содержание которой приведены на рисунке 1.

Надписи, а также буквенные и цифровые обозначения на чертежах выполняются стандартным шрифтом согласно ГОСТ 2.304-81. Графическое условие и решение каждой задачи необходимо вычерчивать простым карандашом, соблюдая ГОСТ 2.303-68 по начертанию и толщине линий.

Вначале весь чертеж выполняется тонкими линиями твердым карандашом. Необходимую толщину линиям придают при их обводке карандашом М или ТМ. После обводки чертеж должен содержать все вспомогательные построения, которые характеризуют ход решения задачи.

В настоящих методических указаниях помещены образцы выполнения четырех эпюров. Задания для эпюров индивидуальные, представлены в вариантах. Номер варианта соответствует порядковому номеру студента в списке группы. При этом следует учитывать, что приведенные образцы не являются эталонами, а служат примерами расположения на листе и его оформления для одного из возможных способов решения рассмотренных задач.

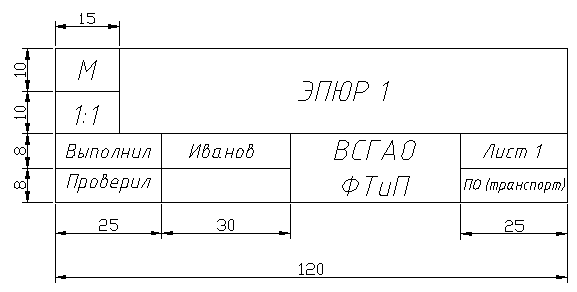
Рис. 1. Основная надпись

Эпюр 1 ПеРесечение двух плоскостей общего положения

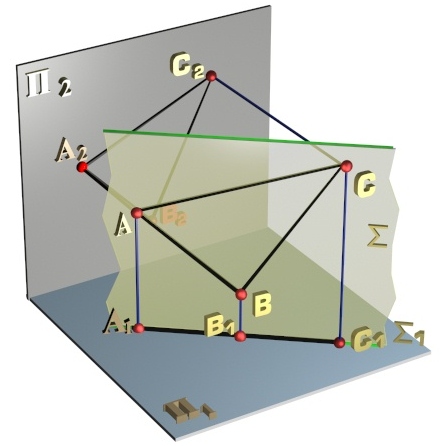
Построить на эпюре и в аксонометрии линию пересечения двух плоскостей, заданных треугольниками (АВС) и (DEF) и определить видимость их сторон. Видимые части проекций треугольников закрасить цветными карандашами светлых тонов, для каждого треугольника – свой цвет.

Координаты точек даны в таблице 1. На чертеже таблицу с координатами точек расположить в любом верхнем углу.

Методические указания к выполнению эпюра 1

Работа выполняется на листе формата А3. Образец выполнения эпюра представлен на рисунке 2.

Если обе пересекающиеся плоскости занимают общее положение, то их линию пересечения можно построить в исходной системе плоскостей проекций, дважды решив задачу на пересечение прямой одной плоскости со второй плоскостью.

На листе формата А3 намечаются оси координат, согласно своему варианту в таблице 1 берутся координаты точек и строятся ортогональные проекции треугольников АВС и DEF. Стороны треугольников и другие вспомогательные прямые проводятся вначале тонкими сплошными линиями.

Задача на построение проекций линии пересечения двух треугольников решается по следующему алгоритму:

а) вводится посредник – фронтально проецирующая плоскость α, через сторону треугольника АВС (в качестве посредника можно взять фронтально проецирующую или горизонтально проецирующую плоскость);

б) линия пересечения плоскости посредника с треугольником АВС – это сторона ВС. Строится линия пересечения плоскости посредника с треугольником DEF, в результате получится какая-то линия, например 1 2;

в) определяется точка N, точка пересечения линий ВС и 1 2. Эта точка является общей точкой треугольников АВС и DEF;

г) для того, чтобы определить вторую общую точку М, необходимо ввести еще один посредник и все построения повторить еще раз.

Видимость треугольников определяют способом конкурирующих точек. Видимость пересекающихся плоскостей на фронтальной плоскости проекций определена с помощью фронтально конкурирующих точек. Для определения видимости на горизонтальной плоскости проекций использованы горизонтально конкурирующие точки.

Видимые отрезки сторон треугольников необходимо выделить сплошными основными линиями, а невидимые – тонкими штриховыми линиями. Линию пересечения треугольников выделить красным цветом. Все вспомогательные построения должны быть обязательно показаны на чертеже в виде тонких линий.

Видимые части треугольников АВС и DEF в ортогональных проекциях закрасить цветным карандашом слабым тоном (каждый треугольник в свой цвет). Все буквенные и цифровые обозначения, а также надписи должны быть четкими и выполнены простым карандашом, чертежным шрифтом.

Таблица 1. Варианты индивидуальных заданий Эпюр 1

(координаты в мм)

Пример выполнения Эпюра 1.

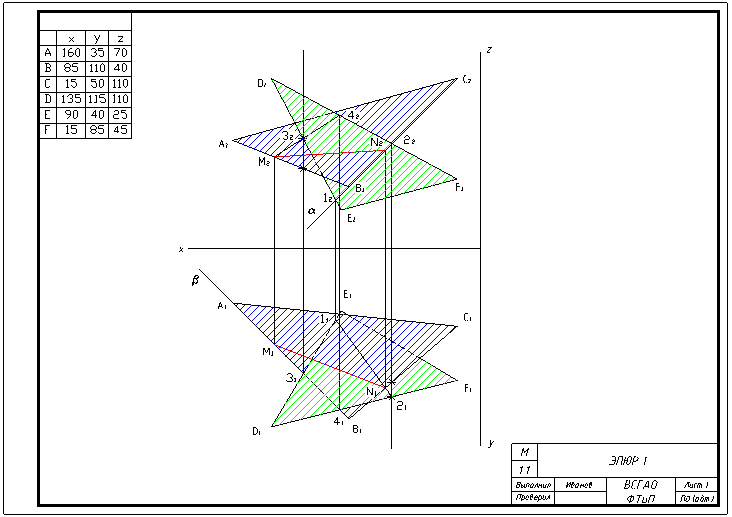
Рис. 2.

Эпюр 2 методы преобразования чертежа

1. Построить проекции пирамиды, основанием которой является треугольник АВС, а ребро SА определяет высоту пирамиды h.

2. Определить кратчайшее расстояние между прямыми SA и ВС (метод замены плоскостей проекций).

3. Найти натуральную величину плоскости АВС (метод вращения вокруг линии уровня).

Координаты точек приведены в таблице 2. Пример выполнения представлен на рис.3 и рис.4.