История развития и современное состояние применения математических методов в географических исследованиях. Впервые математические методы в географии предложено было использовать в 20-е годы ХХ в. российскими географами В. П. Семеновым-Тян-Шанским и М.М. Протодьяконовым. Положительно отозвался о возможности применения математики в географии академик А. А. Григорьев в 1934 г. Пионером внедрения математики в географию является Д. Л. Арманд (1949). Первая работа, посвященная использованию математической статистики в географии, была опубликована В. А. Червяковым (1966).

Конец 50-х - 60-е гг.- расцвет математизации. Множество географов работают под лозунгом: "Математические методы решают все". Без математических выкладок несолидно было издавать книги или защищать диссертации. Большое влияние в нашей стране на математизацию второй половины 60-х гг. оказало появление математических школ для географов. В программах большинства конференций и съездов появляются секции по применению математических методов и даже проводятся специальные всесоюзные совещания на тему: "Математические методы в географии", "География и математика" и т. д.

Успехи применения математических методов в географии позволили в 1968 г. на базе Московского государственного университета провести первое Всесоюзное совещание по данной проблеме. В решении совещания обращалось внимание на необходимость фундаментальной подготовки молодых специалистов в области математики.

Дальнейшее развитие всех областей географической науки дает возможность использовать в экспериментах многие разделы математики (теория вероятности, теория информации, линейное программирование, теория графов, теория игр).

Основоположником практического использования линейного программирования является академик Л. В. Канторович. Им разработаны методы решения транспортных задач, а сетевая постановка – с использованием теории графов.

Практическое использование теории графов разработано венгерским математиком Д. Кенигом (1936), спустя 200 лет после разработки теории графов швейцарским математиком Л. Эйлером (1736).

С 1978 г. выходят учебные пособия в издательстве Московского университета В. С. Михеевой по использованию математических методов в экономической географии (методы линейного программирования и теория графов).

В настоящее время основные математические методы анализа обеспечены программными продуктами для ПЭВМ. Простейшие статистические расчеты можно выполнять с помощью Microsoft Excel, входящего в состав Microsoft Office. Однако лучшие результаты дает использование специализированного программного обеспечения. Наиболее распространенными и универсальными статистическими программными пакетами являются Statistica, Systat, NCSS, SPSS. Пакеты различаются в деталях, версиях, полнотой представления материала. Наиболее полно типичные задачи представлены в пакете статистических программ Statistica.

Из различных разделов современной математики в географии наиболее широко используется математическая статистика. На ее долю приходится не менее 80% всех проведенных экспериментов. Стало обычным делом проведение простого статистического анализа географических данных - вычисление средних квадратических отклонений, дисперсии, коэффициентов вариации, оценка согласия распределений с помощью критериев Пирсона, А. Н. Колмогорова, расчеты прямолинейной и нелинейной корреляции, корреляционных отношений, различных видов регрессий и др. Несколько позднее географы обратились к дисперсионному и дискриминантному анализу, а также анализу временных рядов.

Но особенно широкое распространение нашли известные алгоритмы математической статистики - факторный анализ и метод главных компонент. Не менее популярны статистические алгоритмы классификации географических объектов на основе комплексов характеризующих их показателей. Количество алгоритмов классификаций и их разновидностей очень велико, но все они построены на способах членения исходного множества изучаемых объектов на непересекающиеся подмножества: метод потенциальных функций, метод гиперплоскостей, метод гиперсфер и др.

Математические методы широко используются и в экономической и в физической географии.

Математические методы в экономической географии.

Широко применяется математическая статистика, логика, теория информации, общая теория динамических систем и др.

Рассмотрим особенности обработки динамических рядов.

На первом этапе статистической обработки динамических рядов анализируются основные тенденции (тренд) изменения явления во времени. Используется графическое изображение, которое дает исчерпывающую информацию. Вычисляется комплекс специальных показателей, позволяющих дать количественную оценку динамики анализируемого явления.

Абсолютный прирост или убыль характеризуют изменение явления в единицу или интервал времени. Вычитают из данных последующего периода данные предыдущего. Если ряд возрастает, то прирост считается положительным.

Темп роста или снижения – соотношение в процентах последующего уровня к предыдущему, умноженное на 100. Положительный прирост имеет показатель более 100%, отрицательный – менее 100%.

Темп прироста показывает, на сколько процентов увеличился или уменьшился уровень явления. Отражает относительную скорость изменения явления от одного отрезка времени к другому. Вычисляется путем деления абсолютного прироста на предыдущий уровень либо вычитанием из показателя темпа роста 100. При положительном приросте показатель больше нуля, при отрицательном – меньше нуля.

Абсолютное значение 1% прироста характеризует значение или стоимость 1 % прироста изучаемого явления. Может вычисляться делением абсолютного прироста на темп прироста или делением показателя предыдущего уровня на 100. «Стоимость» 1 % темпа роста и прироста в различных совокупностях разная.

П р и м е р. Число районов г. Минска с высоким уровнем загрязнения атмосферного воздуха в 2004 г. было 4, в 2005 г. стало 8. Темп роста составил 200 %. В г. Новополоцке таких районов в 2004 г. было 10, а в 2005 г. стало 15. Темп роста составил 50 %. Однако в первом случае число неблагополучных районов увеличилось на 4, во втором – на 5. Это говорит о том, что даже в одном динамическом ряду значение 1 % роста и темпа прироста может существенно отличаться на разных отрезках времени.

Показатель наглядности характеризует динамику явления в процентах относительно исходного уровня, который принимается за 100. В отличие от других показателей стоимость одного процента здесь остается неизменной. Однако динамика изменения исходных данных от одного промежутка времени к другому становится менее выразительной. Существуют различные варианты вычисления показателей динамики. Они отличаются набором исходных данных и трудоемкостью вычислений (табл. 10.2).

Примеры расчета показателей, представленных в табл. 10.2.

Абсолютный прирост в 1986 и 1987 годах:

А₈₆= У₈₆ – У₈₅ = 90,2 – 65,8 = 24,4; А₈₇ = У₈₇ – У₈₆ = 67,4 – 90,2 = –22,8.

Темп роста в 1986 и 1987 годах:

Т₈₆ = (У₈₆ / У₈₅) · 100 = (90,2 / 65,8) · 100 = 137,1;

Т₈₇ = (У₈₇ / У₈₆) · 100 = (67,4 / 90,2) · 100 = 74,7.

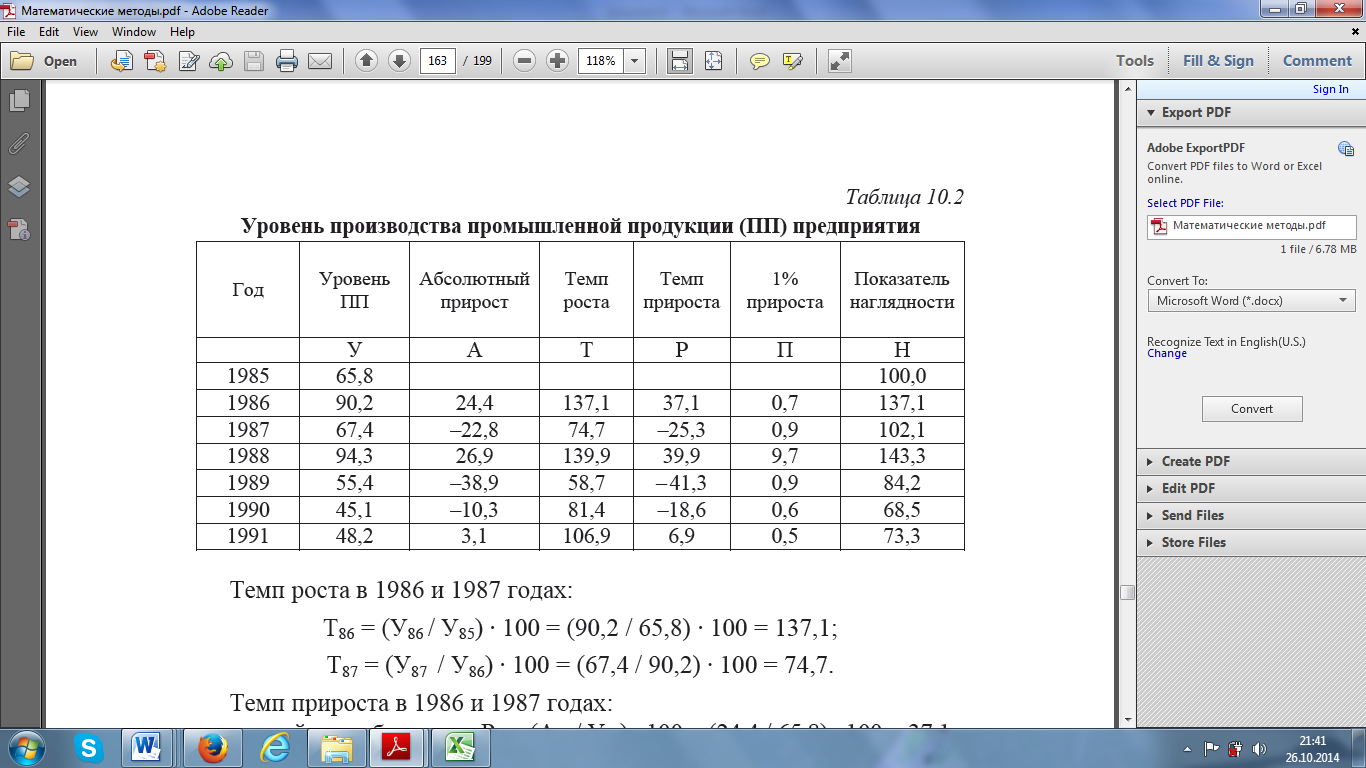
Темп прироста в 1986 и 1987 годах:

первый способ расчета: P₈₆ =(A₈₆ / У₈₅) · 100 = (24,4 / 65,8) · 100 = 37,1;

Р87 = (A₈₇/ У₈₆) · 100 = (–22,8 / 90,2) · 100 = –5,3;

второй способ расчета: P₈₆ = T₈₆ – 100 = 137,1 – 100 = 37,1;

P₈₇ = T₈₇ – 100 = 74,4 – 100 = –25,3.

Абсолютное значение 1 % прироста в 1986 и 1987 годах:

первый способ расчета: П₈₆ = У₈₅ / 100 = 65,8 / 100 = 0,66;

П₈₇ = У₈₆ / 100 = 90,2 / 100 = 0,9;

второй способ расчета: П₈₆ = A₈₆ / P₈₆ = 24,4 / 37,1 = 0,7;

П₈₇ = A₈₇ /P₈₇ = –22,8 / –25,3 = 0,9.

Показатель наглядности прироста в1986 и 1987 годах по сравнению с 1985 г.:

H₈₆ = (У₈₆ / У₈₅) · 100 = (90,2 / 65,8) · 100 = 137,1;

H₈₇ = (У₈₇ / У₈₅) · 100 = (67,4 / 65,8) · 100 = 102,4.

Средний абсолютный прирост: М = (A₈₅ + A₈₆ + … + A₉₁) / n.

Средний темп прироста (среднее хронологическое) вычисляется в виде среднего геометрического: Мг = n P₈₅ ⋅ P₈₆ ⋅ ... ⋅ P₉₁.

Динамический характер всех используемых показателей может принимать самые разнообразные формы. Например, абсолютные приросты могут быть стабильными, а темпы роста (прироста) при этом увеличиваться или уменьшаться.