Вычисление криволинейных интегралов по координатам
Вычисление криволинейного интеграла по координате сводится к вычислению обычного определенного интеграла. Для этого надо все координаты x, y, z и их дифференциалы dx, dy, dz выразить через переменную, принятую за основную в задании кривой Г, и ее дифференциал. Пределы интегрирования должны соответствовать направлению обхода контура интегрирования.
Например, если плоская кривая Г задана параметрическими уравнениями
t,
причем установленное по кривой Г движение от А к В соответствует изменению переменной t от до , то
(в этом случае t – основная переменная в задании кривой Г).
Пример.
Вычислить
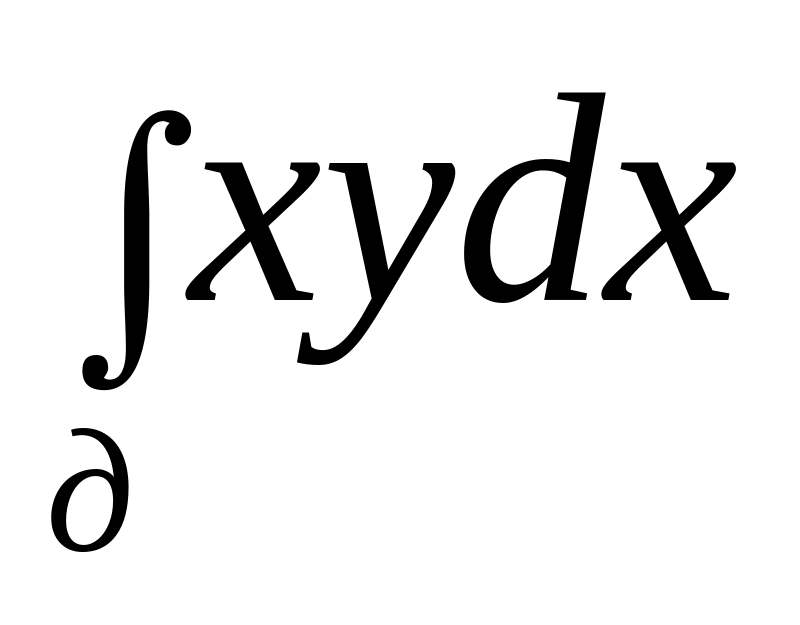по параболе x=y2
от точки (9,–3) до точки (1,1).
Решение. Кривая Г задана уравнением x=y2 ,и установленное по кривой движение соответствует изменению основной переменной y от –3 до 1. Поэтому
.
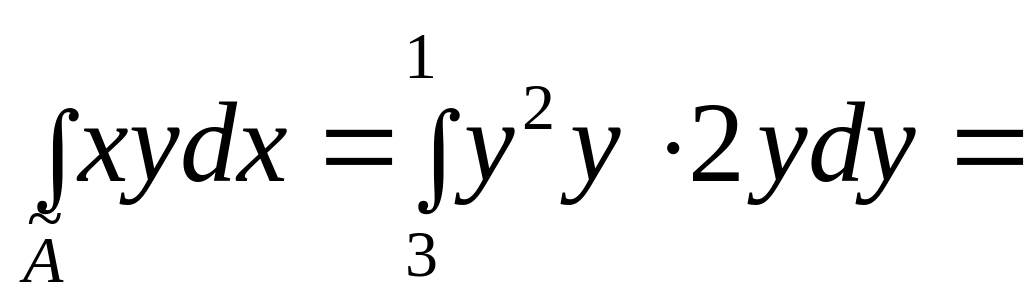
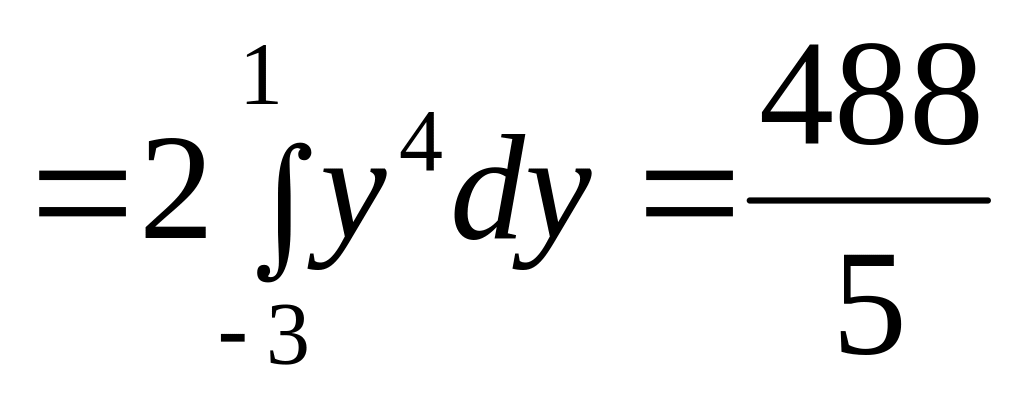