Вычисление криволинейных интегралов

Вычисление криволинейного интеграла сводится к вычислению обычного определенного интеграла, если воспользоваться известными формулами для дифференциала длины дуги dL.

Рассмотрим сначала плоскую кривую Г, по которой требуется вычислить (рис. 2.6). Пусть линия Г задана уравнением у=(x), axb. Тогда

.

Рис. 2.6 Рис. 2.7

Если кривая Г задана уравнением x=(y), где сyd (рис. 2.7), то

.

Если кривая Г задана параметрическими уравнениями , t, то , и тогда

.

В случае, когда плоская кривая Г задана полярным уравнением r=r(), ,

.

Для пространственной кривой Г, заданной параметрическими уравнениями x=x(t), y=y(t), z=z(t), t, справедлива формула

.

Заметим, что при вычислении криволинейного интеграла нижний предел соответствующего определенного интеграла должен быть меньше верхнего, так как элемент dL длины дуги всегда должен быть больше нуля.

Пример. Найти массу участка кривой y=lnx от точки с абсциссой до точки с абсциссой , если плотность массы в каждой точке равна квадрату ее абсциссы.

Решение. Имеем: . Так как кривая задана уравнением y=lnx, x , то получаем:

.

Рис. 2.8

Пример. Найти длину первого витка винтовой линии , , z=bt (рис. 2.8)

Решение. Имеем:

.

Вычисление двойного интеграла

Рис. 2.9

Если разбить область D на элементарные части прямыми, параллельными координатным осям (x=const, y=const), то площадь бесконечно малого элемента dS, ограниченного двумя парами бесконечно близких параллельных прямых (рис. 2.9) есть dS=dxdy, поэтому двойной интеграл записывают еще так:

Рис. 2.10 Рис. 2.11

.

Предположим, что область D ограничена графиками непрерывных функций y=y₁(x) и y=y₂(x), причем y₁(x)y₂(x), и прямыми x=a и x=b, причем каждая прямая, параллельная оси Oy (кроме, быть может, прямых x=a и x=b), пересекает границу области D в двух точках (рис. 2.10). Нижнюю из этих точек называют точкой входа, а верхнюю  точкой выхода. При этом область D называют правильной в направлении оси Oy.

Тогда

. (2.2)

Выражение, стоящее в правой части формулы, называется повторным (или двукратным) интегралом.

Сначала функцию f(x,y) надо проинтегрировать по y при произвольном, но фиксированном x от точки входа до точки выхода (внутреннее интегрирование по переменной y), а затем полученную функцию проинтегрировать по x в пределах его наибольшего изменения (внешнее интегрирование по переменной x).

Таким образом, для вычисления двойного интеграла нужно произвести последовательное вычисление двух обычных определенных интегралов.

Если область D – правильная в направлении оси Ox (рис.2.11), то

(2.3)

Здесь сначала вычисляется внутренний интеграл 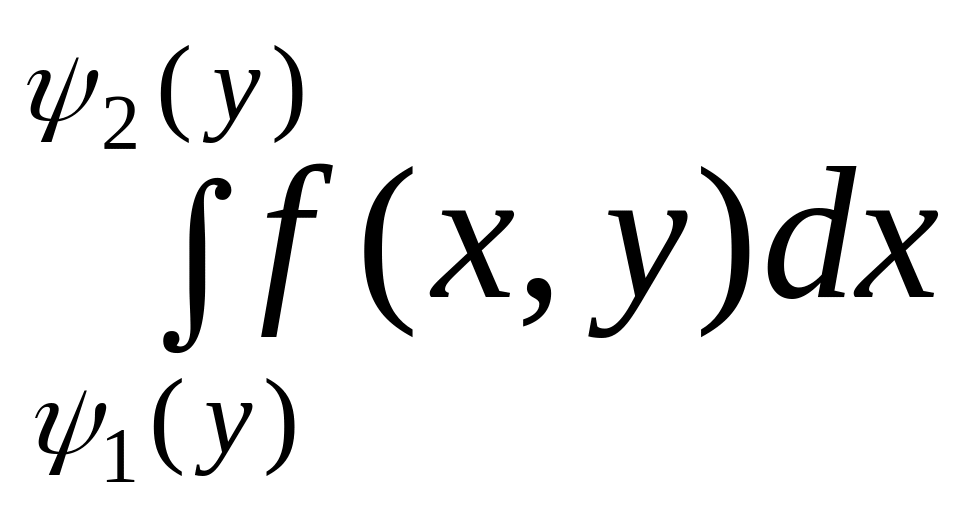по переменной x при произвольном, но фиксированном y. Затем вычисляется внешний интеграл по переменной y в пределах ее наибольшего изменения.

Замечание. Если область D устроена иначе, то надо разбить ее на части, имеющие вышеуказанное устройство, и воспользоваться свойством 3-м аддитивности интеграла.

Пример. Изменить порядок интегрирования в повторном интеграле

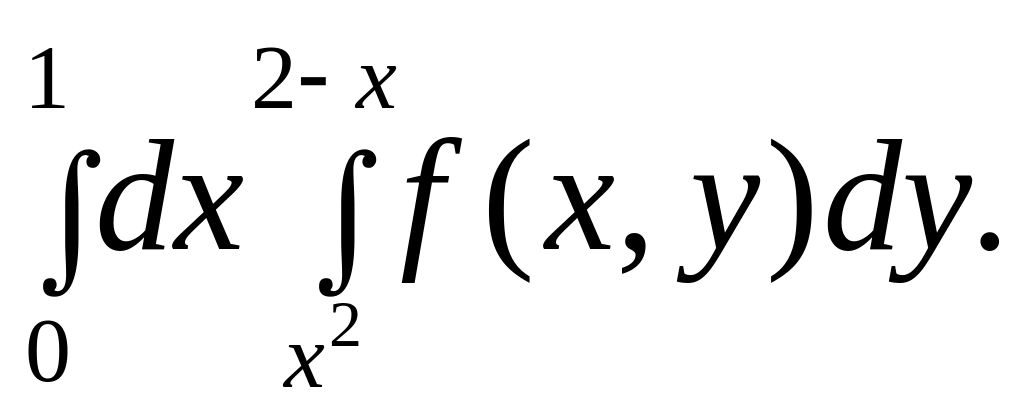
а б

Рис. 2.12

Решение. Этот интеграл равен двойному интегралу от функции f(x,y) по области D, заданной неравенствами 0x1; x²y2–x. Отсюда заключаем, что область интегрирования D ограничена линиями x=0, x=1, y=x² и y=2–x. Часть границы, лежащая на прямой x=1, сводится к одной точке A(1,1) (рис. 2.12, а)).

Для изменения порядка интегрирования проектируем область D на ось Oy. Этим определится отрезок [0,2] изменения переменной y. Так как участок границы OAB области D задан двумя линиями, то прямая y=1 разбивает ее на две области D₁: 0y 0x и D₂: 1y2 x2–y, (рис. 2.12, б).

Здесь уравнения линий OA x= и AB: x=2–y, ограничивающих области интегрирования D₁ и D₂, разрешены относительно переменной x, по которой теперь вычисляются внутренние интегралы.

Взяв сумму интегралов по областям D₁ и D₂, получим

Пример. Вычислить если область D ограничена линиями y=x, y=2x и xy=2.

Рис. 2.13

Решение. Прежде всего построим область D на плоскости xOy. Из рис.2.13 видно, что область D есть сумма двух областей OAC и CAB (D₁ и D₂), правильных в направлении оси Oy. Определив абсциссы точек пересечения прямых OA и OB с гиперболой, по формуле (2.2), учитывая свойство 3 аддитивности интеграла, получаем:

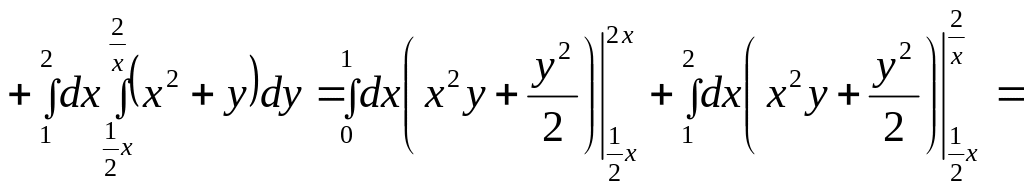
Рис. 2.14

Пример. Найти объем тела, ограниченного поверхностями z=x²+y², y=x², y=1, z=0.

Решение. Построим тело, ограниченное параболоидом вращения z=x²+y², параболическим цилиндром y=x² и плоскостями y=1 и z=0, в прямоугольной системе координат xyz (рис. 2.14).

Тело симметрично относительно плоскости zOy, поэтому можно вычислить половину объема. Тогда объем данного тела