70

Тема 2. Интегральное исчисление функций нескольких переменных

Программный объем темы:

1.Интегральная сумма и определенный интеграл по фигуре. Виды интегралов, их обозначения и названия.

2.Механический смысл интеграла. Задача о массе фигуры и ее решение.

3.Геометрический смысл двойного интеграла.

4.Основные свойства определенного интеграла по фигуре.

5.Вычисление определенных интегралов по фигуре.

6.Приложения определенного интеграла по фигуре в механике.

7.Криволинейные интегралы II рода.

Рассмотрим единый подход к определению различных интегралов для функций нескольких переменных.

ИНТЕГРАЛЬНАЯ СУММА И ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

ПО ФИГУРЕ

Фигура. Диаметр. Мера

Рис. 2.1 Рис. 2.2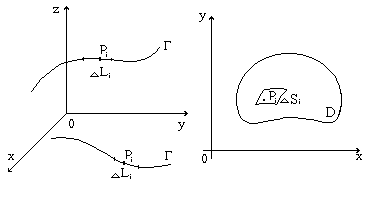

Будем называть фигурой  либо линию в пространстве или на плоскости (рис. 2.1), либо плоскую область (рис. 2.2), либо поверхность в пространстве (рис. 2.3), либо пространственное тело (рис. 2.4). Все рассматриваемые линии (Г, границы поверхностей D и Q) будем считать кусочно-гладкими кривыми.

Рис. 2.3 Рис. 2.4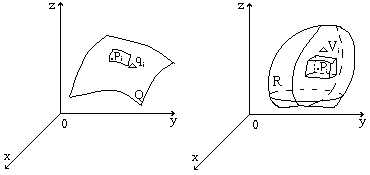

Диаметром фигуры будем называть максимальное из расстояний между точками этой фигуры. Например, для плоской области, ограниченной эллипсом, диаметр равен большой оси этого эллипса; диаметр куба – длине его диагонали. Для круга и шара, диаметр, определенный выше, равен диаметру в обычном смысле этого слова.

Рассматривая различные фигуры, будем говорить об их мере. В случае линий (рис. 2.1) под мерой понимается их длина; под мерой поверхностей (рис. 2.3) и, в частности, плоских областей (рис. 2.2) - площадь. Мерами пространственных тел (рис. 2.4) будут объемы этих тел. Рассмотрим только фигуры конечного диаметра (ограниченные фигуры).

Интегральная сумма и определенный интеграл по фигуре

Пусть в каждой точке P фигуры Ф определена функция f(P). Когда фигура – плоская область D или плоская кривая Г, точка P задается двумя координатами (x,y), и f(P) есть функция двух переменных: f(P)=f(x,y). В остальных случаях точка P зависит от трех координат (x,y,z), и функция f(P)=f(x,y,z) есть функция трех переменных.

Разобьем фигуру произвольным образом на конечное число n элементарных частей. Эти части и их меры обозначим одинаковым образом: _1, _{2, ...,} _n, а наибольший из диаметров частей обозначим .

В каждой части _i выберем произвольную точку P_i, вычислим f(P_i) и умножим значение f(P_i) на меру соответствующей части _i. Затем составим сумму

f(P₁)₁+f(P₂)₂+...+f(P_n)_n= . (2.1)

Полученная в результате перечисленных операций сумма (2.1) называется n-й интегральной суммой.

При заданном числе n частей, на которые дробится фигура Ф, можно составить сколько угодно n-х интегральных сумм.

Определенным интегралом по фигуре Ф от заданной на ней функции f(P) называется предел n-ой интегральной суммы, когда стремится к нулю наибольший из диаметров частей, на которые дробится фигура при составлении интегральных сумм. Подразумевается, что этот предел не зависит от способов разбиения фигуры на части и выбора точек P_i.

(при этом число частей n;  _i стягиваются в точки Р_i).

Функция f(P) называется интегрируемой функцией, а f(P)d  подынтегральным выражением.

В случае когда фигура  линия Г, интеграл обозначается так:

.

Этот интеграл называется криволинейным интегралом по длине дуги.

Согласно определению интеграла получаем соответственно для плоской и пространственной линии следующие равенства:

;

(обозначения ясны из рис. 2.1).

Когда фигура  плоская область D, интеграл называется двойным и обозначается

.

Если фигура  поверхность Q, то интеграл обозначается

.

и называется поверхностным.

В случае пространственного тела R интеграл называется тройным и обозначается

.

Таким образом,

= ;

= ;

=

(обозначения ясны из рис. 2.2-2.4).

Достаточным условием существования определенного интеграла по фигуре является непрерывность интегрируемой функции f(P) на замкнутой, то есть включающей границу, и ограниченной фигуре Ф.