Xliv Всероссийская олимпиада школьников по физике. Муниципальный этап. Возможные решения задач

10 Класс

Задача 1. Удачная бомбардировка.

1 Вариант решения

Расположим систему координат так, чтобы ось y была направлена вверх из точки, находящейся на уровне моря под бомбардировщиком в момент метания, а ось x направлена по курсу движения корабля.

1. Закон движение корабля : 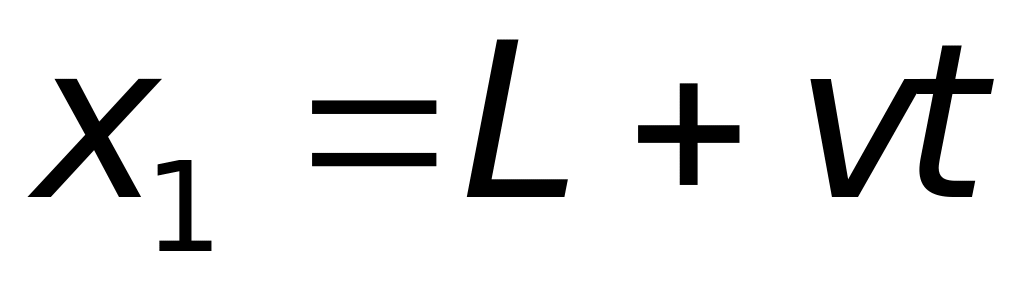; . (2 балла

2. Движение бомбы ; 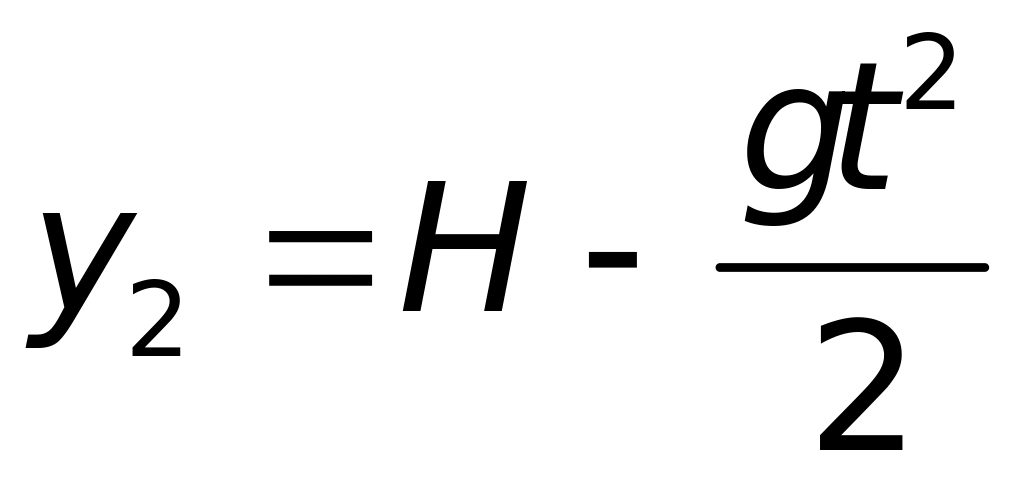. (2 балла)

3. Попадание 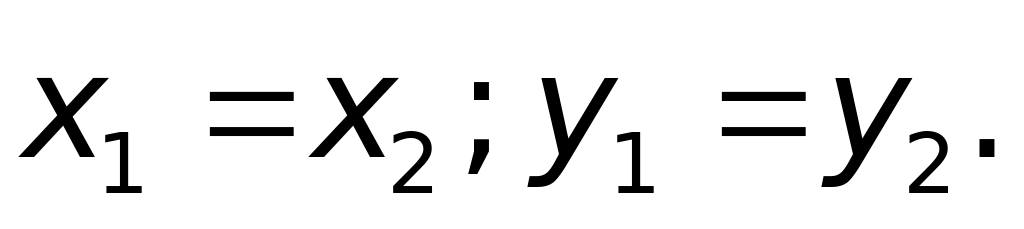(1 балл)

4. Из равенства нулю вертикальной координаты в момент падения находится время падения 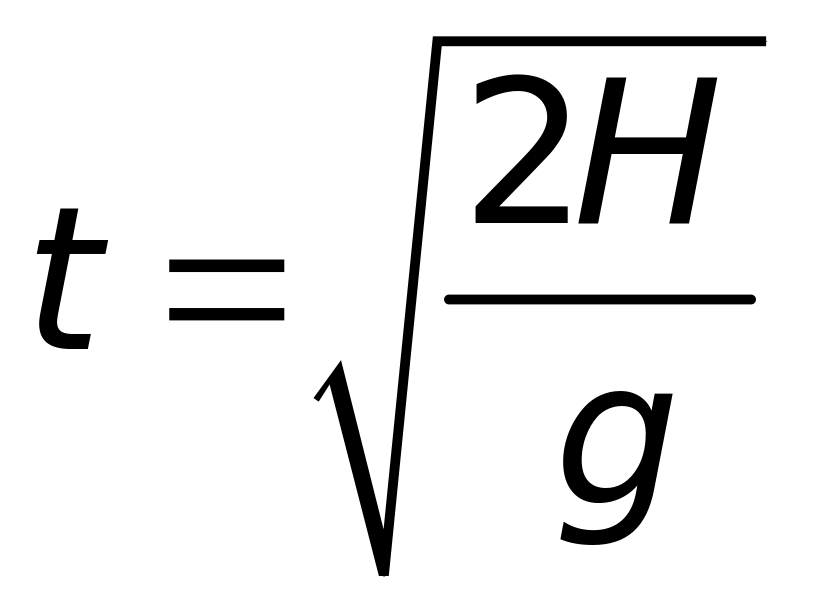. (2 балла)

5. Из равенства горизонтальных координат: . (3 балла)

2 Вариант решения

Расположим систему координат так, чтобы ось y была направлена вверх из точки, находящейся на уровне моря под бомбардировщиком, а ось x направлена по курсу движения корабля.

1. Уравнение траектории тела, брошенного со скоростью v₀ под углом к горизонту, имеет вид:

(6 баллов)

где - начальные координаты тела. Для условий данной задачи v₀ равняется относительной скорости u-v, , , .

2. Тогда получим: 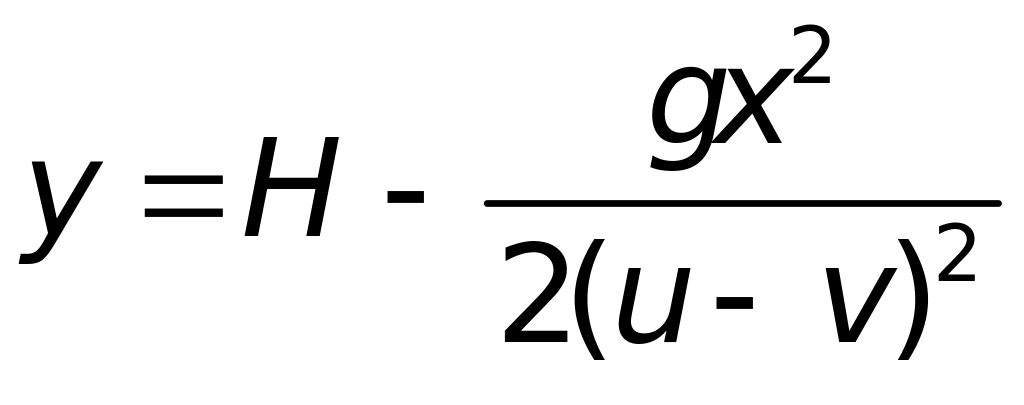(2 балла)

3. откуда из условия падения y=0 следует

(2 балла)

Задача 2. Падение шарика

Шарик движется по дуге окружности до тех пор, пока действующая на него сила реакции стержня не обратится в ноль. Дальнейшее движение до удара о горизонтальную плоскость происходит по параболе – в условиях свободного падения. Найдем сначала положение стержня, при котором сила реакции обращается в ноль.

1. Запишем уравнение второго закона Ньютона в проекции на направление к центру окружности:

(1) (2 балла)

где  - угол между стержнем и вертикалью. Момент отрыва шарика от стержня определяется условием обращения в ноль силы реакции .

2. Входящую в формулу (1) скорость шарика можно выразить с помощью закона сохранения энергии:

(2) (2 балла)

3. Решая совместно уравнения (1) и (2) находим критическое значение угла _, координаты точки отрыва (в системе отсчета связанной с шарниром) и скорость шарика в этот момент:

(3)

, (4)

, (5) (2 балла)

4. Из точки (4) шарик свободно падает в поле тяжести с начальной скоростью (5). Запишем кинематические уравнения, описывающие такое падение:

(6)

5. Используя условие падения , разрешаем второе уравнение в (6) относительно времени и находим время падения шарика из точки (4) до земли:

(7) (2 балла)

6. Тогда искомое расстояние от шарнира до точки падения шарика:

(8) (2 балла)

Задача 3. Металлический шарик на льду.

1. Объем расплавившегося льда равен сумме объемов цилиндра и полусферы:

(3 балла)

2. Количество теплоты, отданное при охлаждении шара, равно

(2 балла)

где - плотность металла, - его теплоёмкость.

3. Количество теплоты, полученное льдом при плавлении равно

(1 балл)

где - масса и плотность льда.

4. По закону сохранения энергии 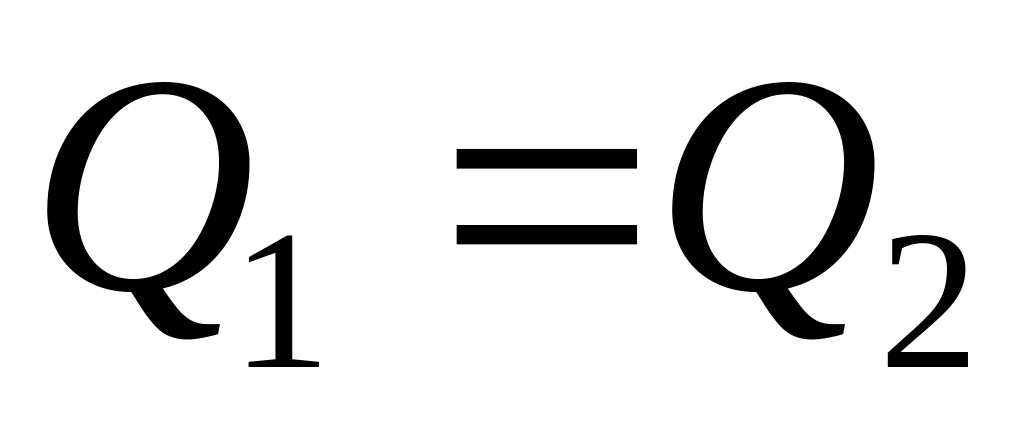, откуда получаем:

=0,93 см (4 балла)

Задача 4. Чему равно сопротивление контура?

1. Из соображений симметрии следует, что напряжение между точками соединения проводников, равноудаленными от точек А и В, равно нулю. И, значит, через проводники, соединяющие эти точки, ток течь не будет и эти проводники можно удалить. (6 баллов)

2. Таким образом, схема сводится к четырем проводникам АВ, соединенным параллельно. Так как их сопротивления одинаковы, то общее сопротивление контура

(2 балла)

3. Сопротивление каждого проводника равно

(1 балл)

где S – площадь поперечного сечения проводника.

4. В результате получим:

(1 балл)