Формальное использование метода Магу:

1. Взять i-ую строку матрицы смежности и записать для нее выражение

, где ;

соответствуют номерам столбцов матрицы, содержащим на пересечении со строкой i единицы.

2. Операцию (п.1) провести для всех строк.

3. Выполнить конъюнкцию полученных выражений и упростить.

4. В итоговом выражении для каждой конъюнкции выписать не вошедшие в нее индексы.

5. Сформировать соответствующие внутренне устойчивые множества и определить число внутренней устойчивости графа .

ПРИМЕЧАНИЯ: А. Петли игнорируются!!!

Б. Пустые строки не учитываются!!!

Для этой же матрицы смежности (R)

( )

Результат тот же

Метод Магу определения числа внешней устойчивости графа.

Внешне устойчивое множество Т – это такое множество вершин графа G, что в каждую вершину x_i графа, не принадлежащую Т, заходит дуга, исходящая из вершины множества Т:

Х – множество всех вершин графа.

Для всех вершин графа выполняется:

Другими словами, любая вершина x_i либо принадлежит внешне устойчивому множеству Т, либо для нее всегда найдется вершина из множества Т, из которой исходит дуга, заходящая в данную вершину x_i.

На основании выше изложенного запишем:

Формула (1) показывает все возможные варианты положения вершины x_i относительно внешне устойчивого множества Т.

Для вершины x_k из множества Т:

(2)

Выполним конъюнкцию левых и правых частей выражений (1) и (2):

(*)

Таким образом, соотношение описывает все возможные способы распределения пары вершин x_i и x_k относительно внешне устойчивого множества Т, т.е. описывает процесс построения всех внешне устойчивых множеств при различных местоположениях вершин x_i и x_k.

Соотношение (1) запишем более формально, приняв новые обозначения: ; Значит, , Получим (1)

В общем виде: - основное соотношение.

(* *)

После раскрытия скобок в последнем выражении (* *) и проведения операции поглощения ( ) получим дизъюнкцию конъюнкций. В каждой конъюнкции перечисляются все вершины графа, образующие минимальные внешне устойчивые множества. Сколько конъюнкций, столько и множеств.

Пример: Дана матрица смежности графа

		1	2	3	4	5
	1		1		1	1
	2			1
R=	3		1			1
	4
	5		1		1

x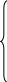 ₁ v x₁ α₁₁ v x₂ α₂₁ v x₃ α₃₁ v x₄ α₄₁ v x₅ α₅₁ = 1

x₂ v x₁ α₁₂ v x₂ α₂₂ v x₃ α₃₂ v x₄ α₄₂ v x₅ α₅₂ = 1

x₃ v x₁ α₁₃ v x₂ α₂₃ v x₃ α₃₃ v x₄ α₄₃ v x₅ α₅₃ = 1

x₄ v x₁ α₁₄ v x₂ α₂₄ v x₃ α₃₄ v x₄ α₄₄ v x₅ α₅₄ = 1

x₅ v x₁ α₁₅ v x₂ α₂₅ v x₃ α₃₅ v x₄ α₄₅ v x₅ α₅₅ = 1

Выпишем все αij:	α11 = 0; α11 = 1; α13 = 0; α14 = 1; α15 = 1;
	α21 = 0; α22 = 0; α23 = 1; α24 = 0; α25 = 0;
	α31 = 0; α32 = 1; α33 = 0; α34 = 0; α35 = 1;
	α41 = 0; α42 = 0; α43 = 0; α44 = 0; α45 = 0;
	α51 = 0; α52 = 1; α53 = 0; α54 = 1; α55 = 0;

Перемножаем и выписываем в строку (конъюнкция):

x1 = 1
x2 v x1 v x3 v x5 = 1	x2 v x3 v x5 = 1
x3 v x2 = 1
x1 v x4 v x5 = 1
x5 v x1 v x3 = 1	x1 v x5 v x3 = 1

x₁ (x₂ v x₃ v x₅)(x₃ v x₂)(x₁ v x₄ v x₅)(x₁ v x₃ v x₅) = 1

(x₂ v x₃)(x₂ v x₃ v x₅)(x₁ v x₃ v x₅)(x₁ v x₄ v x₅) = 1

(x₂ v x₂x₃ v x₂x₅ v x₃ v x₃x₅)(x₁ v x₁x₄ v x₁x₅ v x₁x₃ v x₃x₄ v x₃x₅ v x₁x₅ v x₅x₄ v v x₅) = 1

(x₂ v x₃ v x₂x₅)(x₁ v x₅ v x₁x₄ v x₁x₃ v x₃x₄ v x₃x₅)(x₂ v x₃)(x₁ v x₅ v x₃x₄) = 1

x₁x₂ v x₂x₅ v x₂x₃x₄ v x₁x₃ v x₃x₅ v x₃x₄ = 1

x₁x₂ v x₂x₅ v x₃x₄ v x₁x₃ v x₃x₅ = 1

x₁x₂ v x₁x₂x₅ v v x₁x₃ = 1