Лабораторная работа № 2 Исследование цепей синусоидального тока при последовательном соединении r,l и r,c элементов

1. Цель работы

Проверка основных теоретических соотношений в цепи синусоидального тока при последовательном включении активного и реактивного сопротивлений с помощью программного комплекса EWB.

2. Краткая теория и задания

Рассмотрим процессы, возникающие в резисторе, катушке индуктивности и конденсаторе на примере последовательного соединения R,L и R,C элементов.

2.1 Последовательное соединение резистора и индуктивной катушки

Рассмотрим электрическую цепь, содержащую последовательно соединенные резистор и индуктивную катушку, схема которой изображена на рис. 3.1 а. Пусть цепь подключена к источнику синусоидального напряжения .

Рис. 3.1 а) схема последовательного соединения резистора и катушки индуктивности; б) график изменения тока и напряжения от времени

Если входное напряжение изменяется по синусоидальному закону, то падения напряжения на всех элементах и ток в цепи изменяется также по синусоидальному закону (рис. 3.1 б)

,

где ω=2πf  угловая частота,  начальная фаза тока.

Уравнение по второму закону Кирхгофа для мгновенных значений

или

.

Начальная фаза напряжения на активном элементе совпадает с начальной фазой тока, а начальная фаза напряжения на индуктивном сопротивлении опережает начальную фазу тока на угол .

Синусоидально изменяющаяся во времени функция, изображается вращающимся вектором, длина которого определяется ее амплитудой. Поэтому уравнение можно представить как векторную сумму падений напряжений на активном и индуктивном сопротивлениях

.

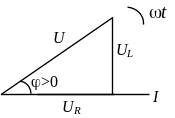_{Рис. 3.2 Векторная диаграмма тока и напряжений}Совокупность векторов, построенных с соблюдением их взаимной ориентацией на фазе, называется векторной диаграммой. Принято отсчитывать углы начальных фаз от горизонтали, а знак угла считать положительным при вращении вектора против часовой стрелки.

Векторная диаграмма исследуемой цепи для тока и напряжений показана на рис. 3.2. Для простоты построения диаграммы начальная фаза тока принята равной нулю.

Вектор напряжения на активном сопротивлении совпадает по фазе с вектором тока, а на индуктивном опережает вектор тока на угол .

Знак угла положительный, если поворот вектора тока к вектору напряжения на наименьший угол совпадает с положительным направлением вращения векторов. Индуктивный характер цепи соответствует положительному значению угла .

Результирующий вектор напряжения на входе рассматриваемой цепи опережает вектор тока на угол , равный разности начальных фаз между входным напряжением и током

.

Если в векторной диаграмме, изображенной на рис. 3.2, все вектора напряжений разделить на общий множитель I, то получим треугольник сопротивлений, изображенный на рис. 3.3.

Рис. 3.3 Треугольник сопротивленийИз векторной диаграммы напряжений рис. 3.2 и треугольника сопротивлений рис. 3.3 получим следующие соотношения:

где [Ом]  реактивное сопротивление индуктивного элемента,  полное сопротивление цепи, [Ом].

,

где  угол сдвига фаз между током и напряжением

, .

Если в векторной диаграмме, изображенной на рис. 3.2, все вектора напряжений умножить на общий множитель тока I, то получим треугольник мощностей, изображенный на рис. 3.4.

Рис. 3.4 Треугольник мощностей Полная мощность цепи  величина, равная произведению действующих значений электрического напряжения и электрического тока

.

Единицей измерения полной мощности является вольт-ампер, .

Потребляемой в цепи считается активная мощность P. Она рассеивается в виде тепла на активных сопротивлениях цепи

,

где  коэффициент мощности цепи, который показывает, какая часть полной мощности S расходуется в цепи.

Единицей измерения активной мощности является ватт [Вт].

Реактивная мощность цепи  величина, равная при синусоидальных электрическом токе и электрическом напряжении произведению действующего значения напряжения на действующее значение тока и на синус угла сдвига фаз между напряжением и током

.

Единицей измерения реактивной мощности является вольт-ампер реактивный [ВАр].

Задание:

1. Для схемы, состоящей из последовательно соединенных резистора R, катушки индуктивности L и синусоидального источника ЭДС E с частотой Гц (значения R, L и E приведены в индивидуальном задании) рассчитайте: входное полное сопротивление, действующее значение тока в контуре, действующее значение напряжения на каждом компоненте.

2. Запустите EWB.

3. Подготовьте новый файл для работы. Для этого необходимо выполнить следующие операции из меню: File/New и File/Save as.

4. В рабочей области EWB составьте схему как показано на рис. 3.5.

Рис. 3.5 Пример схемы соединения элементов

Для формирования электрической схемы используйте номиналы элементов, которые указаны для расчетов в пункте 1 задания.

Сопоставьте результаты расчетов с показаниями вольтметров и амперметра.

5. По результатам эксперимента и расчетным величинам постройте векторную диаграмму напряжений, треугольник сопротивлений и мощностей.

6. Подключите к цепи осциллограф как показано на рис. 3.6.

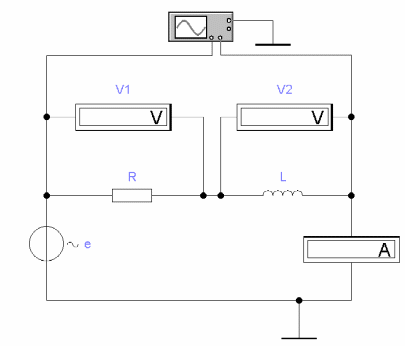
Рис. 3.6 Схема включения осциллографа в исследуемую цепь

7. Введите настройки осциллографа соответствующие Вашей схеме (см. Приложение 3).

8. На расширенной панели осциллографа измерьте угол сдвига фаз между входным и выходным сигналом.

Визирные линии необходимо поставить в точки пересечения синусоид с осью времени. Из правого цифрового табло отсчетов видно, что временной промежуток между визирными линиями составляет . Поскольку период колебаний исследуемых сигналов составляет с (частота 50 Гц), то измеренный промежуток времени, пропорциональный разности начальных фаз, в градусах может быть определен из соотношения:

.

9. Сопоставьте угол сдвига фаз, полученный с осциллографа, с углом сдвига фаз на векторной диаграмме. Допустимо небольшое отклонение показаний осциллографа от расчетного. Разница объясняется погрешностью отсчета временного интервала при установке визирных линий. Она должна составлять не более 5%.

10. Увеличьте сопротивление резистора в два раза. Проследите, как изменятся показания приборов и угол сдвига фаз на осциллографе.

11. Восстановите значение сопротивления резистора. Увеличьте индуктивность в 4 раза. Проследите, как изменятся показания приборов и угол сдвига фаз на осциллографе.

12. Сведите данные измеренных значений в табл. 3.1.

Таблица 3.1

№	Измеренные величины
	R, [Ом]	L, [Гн]	ВХ, [В]	UR, [В]	UL, [В]	I, [В]	, [град]
1 2 3

13. Проверьте полученные экспериментально значения на странице проверки ответов http://toe.ugatu.ac.ru, либо сверьте полученное значение у преподавателя.

14. По пунктам 11 и 12 постройте векторные диаграммы и треугольники сопротивлений и мощностей.

15. Для табл. 3.1 выполните расчеты и полученные результаты представьте в виде табл. 3.2.

Таблица 3.2

№	Расчетные величины (для цепи R, L)
	Z, [Ом]	XL, [Ом]	cos	P, [Вт]	Q, [ВАр]	S, [ВА]
1 2 3

16. Проверьте полученные расчетные значения на странице проверки ответов http://toe.ugatu.ac.ru, либо сверьте полученное значение у преподавателя.

17. Сделайте вывод о влиянии изменения активной и реактивной составляющих на изменение угла сдвига фаз между входным напряжением и током.

2.2 Последовательное соединение резистора и конденсатора

Рассмотрим электрическую цепь, содержащую последовательно соединенные резистор и конденсатор, схема которой изображена на рис. 3.7.

Пусть цепь подключена к источнику синусоидального напряжения .

Рис. 3.7 а) схема последовательного соединения резистора и конденсатора;

б) график изменения тока и напряжения от времени

По второму закону Кирхгофа для мгновенных значений напряжений входное напряжение в рассматриваемой схеме

,

где  начальное напряжение на ёмкости. Если не оговорено особо, то считают .

Из анализа выражения следует, что напряжение на активном элементе совпадает с током по фазе, а начальная фаза напряжения на емкости отстает от тока на угол .

Для векторов напряжений рассматриваемой схемы

.

Векторная диаграмма исследуемой цепи для тока и напряжений показана на рис. 3.8.

При построении диаграммы начальная фаза тока принята равной нулю.

Рис. 3.8 Векторная диаграмма тока и напряжений

Вектор напряжения на активном сопротивлении совпадает по фазе с вектором тока, а на емкостном отстает от вектора тока на угол .

Знак угла отрицательный, что соответствует емкостному характеру цепи.

Результирующий вектор напряжения на входе рассматриваемой цепи отстает от вектора тока на угол , равный разности начальных фаз между приложенным напряжением и током

Если в векторной диаграмме рис. 3.8 все вектора напряжений разделить на общий множитель I, то получим треугольник сопротивлений рис. 3.9.

Рис. 3.9 Треугольник сопротивлений

Из векторной диаграммы напряжений рис. 3.8 и треугольника сопротивлений рис 3.9 получим следующие соотношения:

где  емкостное сопротивление;  полное сопротивление цепи.

Угол сдвига фаз между током и напряжением определяется

.

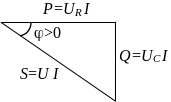
Рис. 3.10 Треугольник мощностей Если все стороны треугольника напряжений умножить на величину тока в цепи, то получиться подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают полную, активную, реактивную мощности – треугольник мощностей.

Задание:

1. Рассчитайте входное полное сопротивление, ток в контуре, напряжение на каждом элементе, для цепи, состоящей из последовательно соединенных резистора R, конденсатора C и синусоидального источника ЭДС E с частотой Гц (значения R, C и E приведены в индивидуальном задании).

2. В рабочей области EWB составьте схему как показано на рис. 3.11.

Рис. 3.11 Пример схемы соединения элементов

Для формирования электрической схемы используйте номиналы элементов, которые указаны для расчета в пункте 1 задания.

3. Сопоставьте результаты расчетов с показаниями вольтметров и амперметра.

4. По результатам эксперимента и расчетным величинам постройте векторную диаграмму напряжений, треугольники сопротивлений и мощностей.

5. Введите настройки осциллографа соответствующие Вашей схеме.

6. На расширенной панели осциллографа измерьте угол сдвига фаз между входным и выходным сигналом.

7. Сопоставьте угол сдвига фаз на осциллографе с углом сдвига фаз на векторной диаграмме.

8. Увеличьте сопротивление резистора в два раза. Проследите, как изменятся показания приборов и угол сдвига фаз на осциллографе.

9. Восстановите значение сопротивления резистора. Увеличьте емкость в 4 раза. Проследите, как изменятся показания приборов и угол сдвига фаз на осциллографе.

10. Занесите данные измеренных значений в табл. 3.3.

Таблица 3.3

№	Измеренные величины
	R, [Ом]	С, [мкФ]	ВХ, [В]		UR, [В]	UС, [В]	I, [В]	, [град]
1 2 3

10. Проверьте полученные экспериментально значения на странице проверки ответов http://toe.ugatu.ac.ru, либо сверьте полученное значение у преподавателя.

11. По пунктам 11 и 12 постройте векторные диаграммы и треугольники сопротивлений и мощностей.

12. Используя данные табл. 3.3 выполните расчеты и полученные результаты занесите в табл. 3.4.

Таблица 3.4

№	Расчетные величины (для цепи R, С)
	Z, [Ом]	XС, [Ом]	cos	P, [Вт]	Q, [ВАр]	S, [ВА]
1 2 3

13. Проверьте полученные расчетные значения на странице проверки ответов http://toe.ugatu.ac.ru, либо сверьте полученное значение у преподавателя.

14. Сделайте вывод о влиянии изменения активной и реактивной составляющих на изменение угла сдвига фаз между приложенным напряжением и током.

3 Контрольные вопросы

1. Как сдвинуты друг относительно друга вектора тока и напряжения на активном сопротивлении, индуктивности и емкости?

2. Как находится полное сопротивление в цепи, содержащей активное и реактивное сопротивления?

3. Как можно определить полную, активную и реактивную мощности?

4. Опишите, как с помощью осциллографа в программе EWB можно измерить угол сдвига фаз между напряжением и током.

5. В цепи с последовательным соединением резистора и индуктивной катушки при неизменном входном напряжении и значении сопротивления резистора увеличивают индуктивность катушки. Как изменится действующее значение тока и напряжение на элементах, активная мощность и угол сдвига фаз между приложенным напряжением и током?

6. В цепи с последовательным соединением резистора и конденсатора при неизменном входном напряжении и значении сопротивления резистора уменьшают емкость конденсатора. Как изменится действующее значение тока и напряжение на элементах, активная мощность и угол сдвига фаз между приложенным напряжением и током?