Фиксированные полюса

Анализ оптимальных систем показывает, что все устойчивые полюса , и автоматически становятся корнями характеристического уравнения оптимальной замкнутой системы. Это – так называемые фиксированные полюса, они определяются особенностями структуры системы. Если эти передаточные функции имеют неустойчивые полюса (с положительной вещественной частью), корнями характеристического уравнения становятся их (устойчивые) отражения от мнимой оси. Если же в , или есть интегрирующее звено, задача не имеет практически ценного решения – характеристическое уравнение «оптимальной» системы будет иметь нулевой корень, система находится на границе области устойчивости.

Полюса функций , и в явном виде не входят в характеристическое уравнение. Для и это объясняется (на интуитивном уровне) тем, что эти блоки находятся вне контура управления. Особенность интегратора с передаточной функцией состоит в том, что входной сигнал проходит через него на выход . Путем достаточно сложных выкладок можно доказать, что при этом его полюса не будут корнями характеристического уравнения. Из этого правила есть одно исключение: формирующий фильтр возмущения не должен содержать дифференцирующее звено, то есть передаточная функция не должна иметь сомножителя в числителе.

Вспомним, что для моделирования воздействия морского волнения чаще всего используют формирующий фильтр с передаточной функцией

,

где – доминирующая частота волн, – коэффициент демпфирования ( ), и – коэффициент, определяющий интенсивность волнения. При этом

,

то есть, полюс в точке сократился нулем передаточной функции . Это значит, что входной сигнал уже не действует на интегратор, и полюс в точке в модели судна должен быть (с формально-математической точки зрения) отнесен к блоку . Так как все полюса (в исходном или «отраженном» виде) становятся корнями характеристического уравнения, в этом случае оптимального стабилизирующего регулятора не существует.

Регуляризация

Что же делать? Нужно построить «квазиоптимальный» (лат. как бы оптимальный, похожий на оптимальный) регулятор, который будет стабилизировать систему, хотя и будет несколько хуже, чем «оптимальный» (но нестабилизирующий!) по выбранному критерию качества. Для этого обычно выполняют регуляризацию задачи, то есть, немного меняют условие так, чтобы она стала решаемой. В данном случае возможно два приема:

1. вместо использовать измененную передаточную функцию фильтра

,

которая не имеет нуля в точке при любом малом ;

2. воспользоваться другой моделью спектра морского волнения, которая дает ненулевое значение на частоте 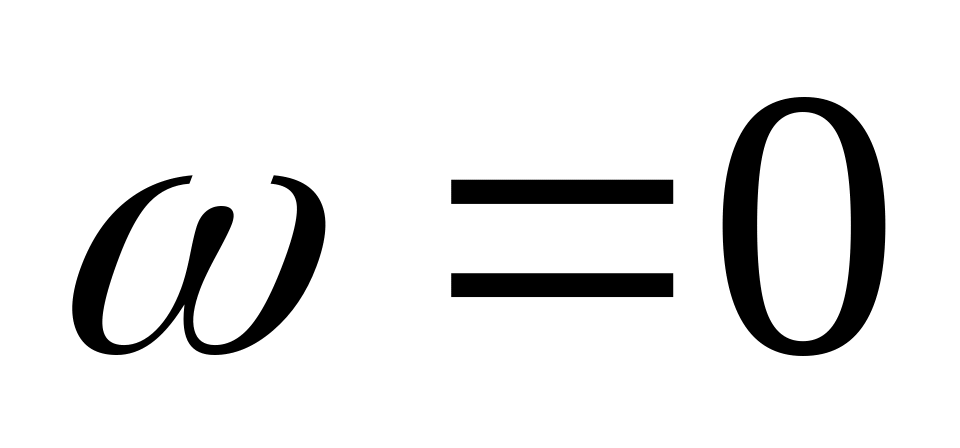, например, дробно-рациональными спектрами типов 1 и 2, которым соответствуют формирующие фильтры

и .

Все не может быть оптимальным

Отметим еще одну особенность рассматриваемой задачи. Мы стремились к тому, чтобы система была устойчива и обеспечивался минимум функции потерь . Одновременно все остальные требования к системе, например, скорость и качество переходных процессов, не учитывались. Поэтому «оптимальный» регулятор может приводить к затянутому или колебательному переходному процессу.