5 Переходный электромагнитный процесс в неподвижных магнитосвязанных цепях

5.1 Общие положения

Многие цепи электрических систем имеют между собой магнитную связь, которая осуществляется через трансформаторы, т.е. аппараты, имеющие специальные магнитные цепи. Протекание электромагнитного переходного процесса в магнитосвязанных цепях имеет некоторые характерные особенности, обусловленные наличием взаимоиндукции.

Принято, что насыщение магнитных систем отсутствует, т.е. собственная и взаимная индуктивности (L и М) элементов являются постоянными величинами. Это позволяет описывать режимы рассматриваемых цепей линейными дифференциальными уравнениями с постоянными коэффициентами.

Характер изменения свободных токов определяется только параметрами элементов рассматриваемой схемы и ее конфигурацией. Поэтому полученные ниже закономерности изменения свободных токов справедливы для любых ЭДС источников питания. Исследования закона изменения свободных токов в магнитосвязанных цепях будем вести при включении их на постоянное напряжение. От закона изменения приложенной ЭДС зависят начальные значения свободных токов.

5.2 Результирующая индуктивность и полное сопротивление двухобмоточного трансформатора в дифференциальной форме

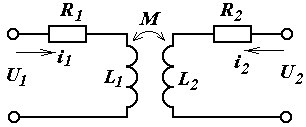
Однофазный двухобмоточный трансформатор представляет собой простейшую цепь с взаимоиндукцией, имеющую всего два индуктивно связанных контура (рис 5.1.). Дифференциальные уравнения для напряжений обмоток трансформатора имеют вид:

(5.1)

где U₁ и U₂ - напряжения на зажимах первичной и вторичной обмоток;

I₁ и I₂ - токи, протекающие по обмоткам;

R₁ и R₂ - активные сопротивления обмоток.

	Потокосцепления обмоток равны сумме собственных потокосцеплений, создаваемых токами, протекающими по рассматриваемой обмотке и потокосцеплений взаимоиндукции: (5.2)
Рисунок 5.1 Двухобмоточный трансформатор

где L₁ и L₂ – полные индуктивности первичной и вторичной обмоток;

М₁₂ = М₂₁ – взаимные индуктивности обмоток, равные друг другу в связи с тем, что обмотки находятся в одинаковых магнитных условиях.

Уравнения для напряжений (5.1) с учетом выражения (5.2) для потокосцеплений обмоток можно записать в виде:

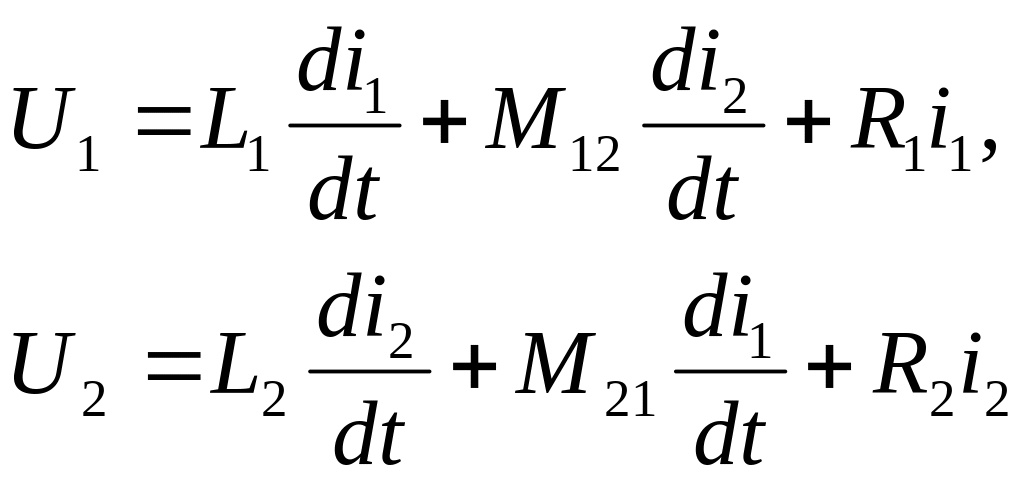(5.3)

При КЗ трансформатора уравнения (5.3) будут для одной фазы:

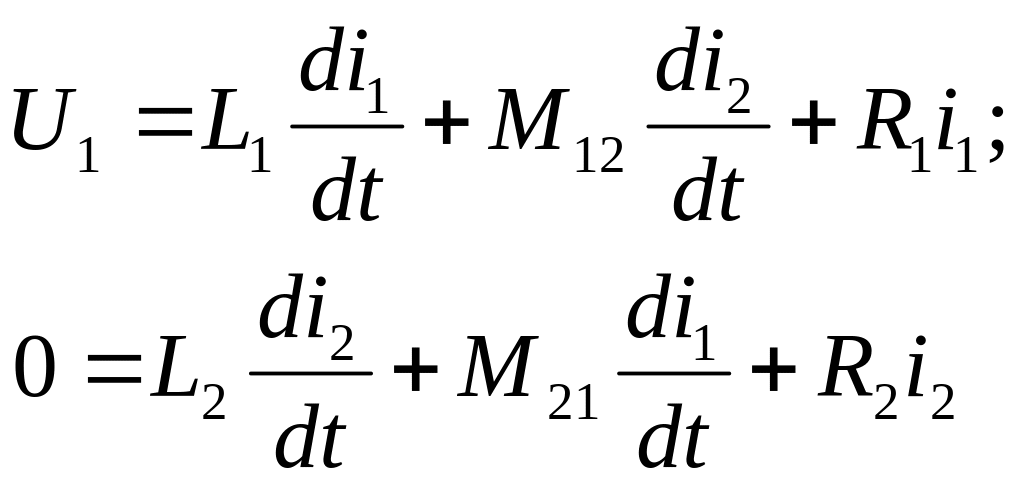(5.4)

Пренебрегая током намагничивания, предположим: i₁ = i₂ = i. Сложим уравнения (5.4), получим:

(5.5)

где R_k=R₁+R₂; L_k=L₁+L₂+2M – активное сопротивление и индуктивность рассеяния трансформатора, обусловленная потоками рассеяния обмоток.

Таким образом, при исследовании процесса КЗ в схеме, содержащей трансформаторы, каждый трансформатор можно рассматривать как обычный элемент электрической цепи со своими сопротивлениями (R_k и L_k) после приведения параметров одной обмотки к другой.

5.3 Уравнения двухобмоточного трансформатора в операторной форме

Для получения операторной формы записи уравнений, то есть для перехода от функций к изображениям, нужно заменить d/dt на оператор р. Уравнения для напряжений первичной и вторичной обмоток трансформатора будут иметь вид:

(5.6)

В этой системе уравнений

(5.7)

где – изображения токов обмоток;

– изображения потокосцеплений обмоток;

– изображения напряжений, приложенных к обмоткам.

На практике при расчетах в системе относительных единиц заменяют само- и взаимные индуктивности равными им в системе относительных единиц при базисной частоте индуктивными сопротивлениями. Для обмоток трансформатора

где Х₁ и Х₂ – полные индуктивные сопротивления обмоток трансформатора;

Х₁₂ – сопротивление взаимной индуктивности обмоток.

Тогда систему уравнений (5.6) можно представить в следующем виде:

(5.8)