§9 Қайталамалы орналастырулар

Осы уақытқа дейін элементтер жиынынан орналастырулар жасағанда одан алынған элемент жиынға қайыра енбейтін еді, ондай орналастырулар болады. Біз енді қайталамалы орналастыруларда, яғни жиыннан алынған элемент сол жиынға қайыра енетінін қарастырамыз, мысалдар келтірейік.

1-мысал. 1,2,3 цифрларынан екі таңбалы неше сан жазуға болады?

Шешуі. Бұл есепті екі тәсілмен шешуге болады.

Бірінші тәсіл: цифрлары қайталанбайтын әр түрлі екі таңбалы сандарды тәсілмен жасаймыз, олар:

1 2 2 1 3 1

13 2 3 3 2

Екінші тәсіл: цифрлары қайталанып отыратын әр түрлі екі таңбалы сандарды біртіндеп жазсақ, мыналар шығады:

1 1 2 1 3 1

1 2 2 2 3 2

1 3 2 3 3 3

Яғни олардың барлық саны 3*3=9 болады. Басқаша аитқанда цифрлардың әрқайсысы да 3 тәсілмен алынады, сонда бірінші алынған цифр әр жолы екінші цифрмен комбинацияланады, сөйтіп, екі цифр комбинациясын

тәсілмен аламыз. Бұл мысалды әрі қарай да кеңете беруге болады.

2-мысал. Осы 1, 2, 3 цифрларын қайталамалы орналастырулар тәсілімен үш таңбалы, төрт таңбалы, k таңбалы неше сан құруға болады?

Шешуі. Үш таңбалы санның бірінші цифрын 3 тәсілмен, екіншісін де 3 тәсілмен алуға болады. Сонда алдыңғы екі цифрлы санды тәсілмен аламыз. Бұлардың әрқайсысы үшінші цифрмен комбинацияланады. Сонда үш цифрлы санды тәсілмен құруға болады. Осылайша талқыласақ, осы үш цифрдан 4 цифрлы сандарды тәсілмен, ал k цифрлы сандарды 3 тәсілмен құруға болатынын байқау қиын емес.

Енді есептің шартын өзгертіп, яғни берілген 1, 2, 3, цифр орнына 1, 2, 3,…., N цифрды алайық. Сонда N цифрдан әр түрлі екі цифрлы сандарды тәсілмен, әр түрлі үш цифрлы сандарды тәсілмен, ал k цифрлы әр түрлі сандарды тәсілмен құруға болады. Сонымен, мынадай қорытындыға келеміз:

Элементтері қайталанып келетін N элементтен k дан алынған орналастырулар

(1)

Формуласымен өрнектеледі. Мұны қайталамалы орналастыру немесе қайталамалы іріктеме формуласы деп айтады.

Қайталанбайтын орналастырулар мен алмастыруларды айтқанда іріктеме көлемі k≤N болатын. Ал, элементтері қайталанатын орналастырулар мен алмастырулар үшін k˂N, k=N және k˃N болуы мүмкін. Бұл факт жоғарыда келтірілген мысалдан айқын көрініп тұр.

§10 Терулер

N элементтен әрқайсысы k дан алынған орналастыруларды бір-бірінен айырмашылығы не элементінде, не элементтің орналасу ретінде ғана болатын дербес түрін алмастырулар дедік. Енді элементтерінің орналасу ретіне көңіл аудармай (яғни мұндай орналастыруларды бірдей деп), айырмашылығы кемінде бір элементінде болатын орналастыруларды қарастырайық. Мұны сысалдан бастайық.

1- мысал. а,b,c әріптерінен элементтерінің орналасу ретін ескермей, айырмашылығы кемінде бір элементінде болатын:

а) екі-екі элементтен неше комбинация жасауға болады;

ә) үш-үш элементтен неше комбинация жасауға болады?

Шешуі. а) a,b,c элементтерден екі-екіден жасалған орналастырулар саны Оларды түгел жазайық:

аb, ba, ca

ас, bc, сb

Бұлардан мынадай үш топқа бөлеміз: ab мен ba, ас мен са, bc мен сb. Әр топқа енетін орналастырулардың айырмашылығы тек элементтерінің тұрған орнында. Мысалы, бірінші топта ab мен ba, екіншісінде ас мен са, үшіншісінде bc мен cb. Әр топтағы орналастырулар саны екі элементтен жасалған алмастыру саны тең. Сонда орналастыруды есе кемітсек , айырмашылығы кемінде бір элементінде болатын орналастырулар саны шығады, олар

аb, ac, bc

б) Үш элементтен үш-үштен жасалған орналастырулар саны

,

олар:

abc, bac, cab,

acb, bca, cba.

Бұлардың барлығы бір ғана топ құрайды, өйткені мұндағы орналастырулардың айырмашылығы тек элементтерінің орналасу ретінде ғана. Осы бір топтың ішіндегі орналастырулар саны үш-үштен жасалған алмастыру саны ! ға тең, сонда орналастыруды есе кемітсек, айырмашылығы кемінде бір элементінде болатын орналастырулар саны болып шығады. Ол- abc тіркесі.

2-мысал. а, b, c, d төрт элементтен орналасу ретін ескермей-ақ, үш элементтен алынған неше комбинация жасауға болады?

Шешуі. 4 элементтен 3 тен алынған орналастырулар саны

Бұлар әр түрлі 4топқа бөлінген, олар мыналар:

1-топ	2-топ	3-топ	4-топ
abc acb bac bca cab cba	abd adb bad bda dab dba	acd adc cad cda dac dca	bcd bdc cbd cdb dbc dcb

Мұндай жеке бір топ ішіндегі орналастырулар тек элементінің орналасу ретімен ғана айрылады. Ал осы 4 топтың бір-бірінен айырмашылығы кемінде бір элементінде, олар:

abc, abd, acd, bcd.

Әр топтың ішіндегі орналастырулардың саны 3 элементтен жасалған алмастырулар саны ! ға тең. Сонда орналастыруларды есе кемітсе, айырмашылығы кемінде бір элементінде болатын орналастырулар саны

болып шығады.

Бұл мысалдардағы 3,4 элемент орнына N элемент алынса, онда орналасу ретін ескермей-ақ, одан k дан алынған

орналастырулар жасаймыз.

Сонымен, N элементтен k дан алынған теру деп, айырмашылығы кемінде бір элементінде болатын орналастыруларды айтамыз. Оны символымен белгілейміз. Сонда

(1)

болады.

Қорыта келгенде, айырмашылығы элементтерінің тек орналасу ретінде болатын орналастыруларды алмастырулар деп, ал айырмашылығы кемінде бір элементінде болатын орналастыруларды терулер дейміз. Орналастыруларда алмастырулар мен терулерде болатын қасиеттер қамтылғандықтан,

(2)

, мәндерін (1) формулаға қойсақ, шығатыны:

(3)

Бұл өрнектің оң жақ бөлігіндегі бөлшектің алымын да, бөлімін де 1*2*3....(N-k) санына көбейтсек,

Яғни

(4)

Формуласы шығады. Бұл формуланы мұнан былай жиі қолданамы, (4) формула N=0 және k=0 мәндерінде де дұрыс болуы үшін 0!=1 деу керектігі естеріңізде болсын. N мен k мәндері үлкен болғанда мәнін (4) формуламен есептеу аса қиынға соғады. Сондықтан факториалдар логарифмдерін паидалану қолайлы. Осы себепті кітаптың соңында 100 факториалға дейінгі сандар логарифмдерінің таблицасын келтірдік(кітап соңындағы 1-таблицаны қара).

3-мысал: N=100, k=50 болғанда мәні неге тең?

Шешуі: енді мұның екі жағын да логарифмдейміз, сонда

lg

1-таблицадан:

lg100! = 157,9700,

lg50! = 64,4831.

Демек,

Бұдан 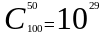өте үлкен сан шығады. Ал ықтималдықтарды есептегенде көп жағдайда N мен k үлкен болып келгенімен, факториалдар логарифмдерін пайдаланып есептеу жеңілге соғады(20-параграфтағы 4- мысалды қара).

Терудің негізгі екі қасиетін келтірейік.

1- қасиеті. (5)

Мұны дәлелдеу үшін (4) формуладағы k орнына N – k қоямыз.

Сонда

(6)

Шығады. (4) және (6) өрнектердің оң жақ бөліктері тең болғандықтан, бұлардың сол жақ бөліктері де тең болады, яғни

(7)

2- қасиеті.

(8)

Мұны дәлелдеу үшін орындарында бұлардың (4) формуладағы мәндерін қойып жазсақ, шығатыны:

Терулердің екінші қасиетін пайдаланып Паскаль үшбұрышы деп аталатын төмендегі схеманы келтіру қолайлы.

Паскаль үшбұрышы

N	k
n=0	k=0	1
n=1	k=1	1 1
n=2	k=2	1 2 1
n=3	k=3	1 3 3 1
n=4	k=4	1 4 6 4 1
n=5	k=5	1 5 10 10 5 1
n=6	k=6	1 6 15 20 15 6 1

Бұл үшбұрыштың құрылысымен танысқанда мынадай ережені байқау қиын емес: төменгі қатардағы әрбір сан (екі шеткісін қоспағанда) оның үштіңгі қатарындағы (сол цифрдың үстіндегі) оң жақ және сол жақ екі санның қосындысына тең, яғни мәні N- қатар үстіндегі N—1 қатарындағы теру мәндеріне сәйкес (7)-ші формула негізінде табылған. Сонымен, мәні N қатары мен k диагональдың қиылысуындағы санға тең. Мысалы, N=8, k=3 болғанда, мәні 8- қатар мен k=3-ке сәйкес диагональдағы 56 санына тең.

Әрбір қатардағы сандар қосындысы санына тең. Мысалы, N=3 болғанда

1+3+3+1=8= ,

N=7 болғанда 1+7+21+35+35+21+7+1=128= т.с.с

Ескерту. Жоғарыда келтірілген алмастыру, орналастыру және теру формулаларын математикалық индукция тәсілімен дәлелдеуді И. С. Соминский кітапшасынан қараңыздар.

$ 11.КОМБИНАТОРИКА ФОРМУЛАЛАРЫН ЫҚТИМАЛДЫҚТАРДЫ ТІКЕЛЕЙ ЕСЕПТЕУГЕ ПАЙДАЛАНУ

1-МЫСАЛ.Жәшікте бірдей он шар бар.Олардың 4-уі ақ түсті, 6-уы қызыл түсті.Екі шар алынды.Екеуінің қызыл түсті болу ықтималдығын анықтау керек.

Шешуі.Есеп шешуінің екі вариантын көрсетейік.

Бірінші вариант.Бірінші алынған шар жәшікке қайта салынбайды,демек,екі шарды А²₁₀=10*9=90 тәсілмен ала аламыз.Қолайлы жағдайлар саны m=6*5=30

демек,

р(A)=6*5/10*9=30/90=1/3=0,33

Екінші вариант .Жәшіктен алынған шардың түсін көргеннен кейін,ол - жәшікке қайта салынады.Бұл жағдайда екі шарды 10²=100 тәсілмен ала аламыз .Мұның ішінде бізге қолайлысы екеуі де қызыл түсті шар болуы түсінікті ,оны 6²=36 тәсілмен ала аламыз.Сондықтан мұның ықтималдығы

р(A)=36/100=0,36.

2-мысал.Соғылатын телефонның номері 4 цифрдан (орыннан) құралған .Ол номердің :a)барлық цифрлары әр түрлі болу келу ықтималдығын,ә)барлық цифрлардың жұп болып келу ықтималдығын анықтау керек.

Шешуі.а)4 таңбалы номердің әр цифры 0,1,2,3,4,5,6,7,8,9 цифрларының кез келгені болуы мүмкін.Олай болса ,әр түрлі төрт таңбалы номерлердің барлық саны 10⁴ болады.Олар 0000-ден 9999-ға дейінгі номерлер саны.Бұлардың ішінде бізге қажеттісі -цифрлары әр түрлі төрт таңбалы сандар,олар 10 цифрдан 4-тен алынған орналастырудың санына тең ,яғни

А₁₀⁴=10*9*8*7

саны.Оқиғалардың барлық тең мүмкіндікті,қос қостан үйлесімсіз және оқиғалардың толық тобын құрайтын нәтижелердің жалпы саны

n=10⁴

демек,оның ықтималдығы

p(A)=10*9*8*7/10⁴=5040/10⁴=0,504

ә)2,4,6,8 төрт жұп нөмірден әр түрлі 4⁴ төрт таңбалы нөмір құрастыруға болады,бұл оқиғаның пайда болуына қолайлы жағдайлар саны m-ге тең.Олай болса, оның ықтималдығы

p(A)=4⁴/10⁴=256/10⁴=0,0256.

3-мысал.Дөңгелек үстел басында отырған 12 адамның туған жылдары қазақша бір мүшел деп аталатын 12 жыл ішінде болсын дейік.Осы 12 адамның әрқайсысының туған жылы 12 жылдың әрбір жылына келу ықтималдығын анықтау керек.

Шешуі.12 адамның әрқайсысынан сұрадық дейік.Сонда бірінші отырған адамның туған жылы 12 жылдың бірі болуы мүмкін ,яғни бірінші сұралған адамның туған жылы туралы 12 түрлі тең мүмкіндікті нәтижелер шығады.Екінші адамның да туған жылы сол 12 жылдың бірі.Бірінші адамның туған жылы жайлы табылған нәтижелер екінші адмның әрбір мүмкін болтын туған жылымен комбинацияланып келеді.Сонда екі адамнан сұрай келе туған жылдар туралы

12*12=12²

тең мүмкіндікті нәтижелер шығарып аламыз.Ал үш адамнан сұрасақ 12²*12=12³ тең мүмкіндікті нәтижелер т.т табамыз.Ал 12 адамнан түгел сұрағанда барлық тең мүмкіндікті нәтижелер саны

n=12¹²

болады.

Енді осылардың ішінде туған жылдары әртүрлі болуға қолайлы жағдайлар саны m-ді есептейік.

Бірінші адамның туған жылы сол 12жылдың кез келген бірі ,ал екінші адамның туған жылы болса ,бос 11 жылдың бірі болады ,үшінші адамның туған жылы қалған 10 жылдың бірі болады т.т Ең соңғы адамның туған жылы қалған жылға келеді.Бұлар бір бірімен комбинацияланып келетіндіктен ,қолайлы жағдайлар саны мынаған тең :

m=12*11*10...2*1=12!

демек ықтималдығы

p(A)=12!/12¹²=0,000054.

4-мысал.9 этажда <<Алматы >> қонақ үйінің бірінші этажынан лифтіге 3 адам мінді.Бұлардың әрқайсысының кез келген этажда түсу мүмкіндіктері бірдей деп алып ,мына ықтималдықтарды анықтау керек:

а)Үшеуінің де 5-этажда түсу ықтималдығы неге тең?

ә)үшеуінің кез келген бір этажда түсу ықтималдығы неге тең?

б)екеуі бірге кез келген бір этажда,ал үшіншісі кез келген өзге этажда түсу ықтималдығы неге тең?

Шешуі.Адам саны 3,эхтаж саны -8 (өйткені бірінші этаж есепке алынбайды )... 2-мысалдағыдай талқыласақ,барлық тең мүмкіндікті жағдайлар саны n=8³ болады.а)5-этаж біреу-ақ.Демек,мұның ықтималдығы

р(A)=1/8³=1/512

a)3 адамды лифтімен 8 этаждың әрқайсысына С³₈ тәсілмен шығаруға болады,яғни m=C³₈.Олай болса,

р(A)=C³₈/8³=8!/3!*5!/512=7/64

б)Екі адамды 8 этаждың әрқайсысына С³₈ тәсілмен шығаруға болады,ал бір адам С₈¹ тәсілмен шығарылады.Бұлардың комбинациясы С₈²*C¹₈=m.Демек ,іздеген ықтималдық мәні

р(A)=C²₈*C¹₈/8³=7/16

5-мысал.Жәшікте бірдей N нәрсе бар .Олардың M нәрсесі жарамды да ,N-M=D нәрсесі жарамсыз .Жәшіктен кез келген S нәрсе іріктелінеді.Іріктеменің m-і жарамды,d-сі жарамысыз нәрсе болу ықтималдығын анықтау керек.

Шешуі:N нәрседен S іріктемені С_N^S т2с3лмен алу5а болады.Бұл нәтижелер барлық тең мүмкіндікті оқиғалар .Қолайлы жағдайлар санын анықтайық.Жарамдыны тек жарамды нәрселерден С^m_M тәсілмен аламыз,ал жарамысызды тек жарамсыз нәрселерден С^d_D немесе С^s-m_N-M тәсілмен аламыз.Алынған S іріктемеде жарамды да ,жарамсыз да нәрселер болуы мүмкін.Олардың шығу комбинациясы С_M^m*C^s-m_N-M тең.

Демек мұның ықтималдығы

р(A)=C_M^m*C^s-m_N-M/C_N^S

6-мысал.преферанс ойынында 32 картаны он оннан үш адамға таратып ,екеуін төңкеріп қояды.Осы төңкеріп қойған карталардың:а)екеуі де тұз болу ықтималдығы неге тең?ә)біреуі тұз, біреуі дама болу ықтималдығы неге тең?

шешуі.32 картадан 2 картаны

С²₃₂=32!/2!*30!=496 тәсілмен алуға болады .

Бұл n-ге тең.а)Қолайлы жағдайлар санын тек тұздардың ішінен анықтаға болады.Колододағы тұздар саны -4, бұлардан екі екіден тұздард С²₄ тәсілмен ала аламыз,олай болса,

m=C₄²=4!/2!2!=6

Демек,іздеген ықтималдық

р(A)=6/496=0.012

ә)1 тұзды 4 тұздан С₄¹ тәсілмен ,1 даманы 4 дамадан С¹₄ тәсілмен аламыз.Бұл екеуінің комбинациясы-С₄¹*С¹₄

демек,

р(А)=С₄¹*С¹₄/С₃₂²=16/496.

Жаттығулар

1.Магазинде 5 сорттан тұратын конфет және 4 сорттан тұратын печенье бер .Бір сорттан тұратын конфет пен бір сорттан тұратын печеньені неше тәсілмен сатып алуға болады ?

2.Кітапхананың сөресінде математикадан 20 кітап, физикадан 12 кітап ,биологиядан 10 кітап бар.Әр түрінен бір бір кітаптан үш кітапты неше тәсілмен алуға болады?

3.0,1,2,3,4,5,6,,7,8,9, цифрларынан , бірінші орында 2 цифры тұратын ,ал келесі орындарда 2-ден өзге кез келген цифр тұратындай етіп, 5 таңбалы телефон нөмірлерін неше тәсілмен құрастыруға болады?

4.Жатақханада 20 оқушы тұрады.Күніне екі оқушыны кезекші етіп неше тәсілмен қоюға болады?

5.Колхоз басқармасына сайланған 11 адамнан колхоз бастығы мен екі орынбасарын және хатшысын (басқарма мүшелерінің әрқайсысының сайлану мүмкіндігі бірдей деп) неше тәсілмен сайлауға болады?

6.Қазақ алфавитінен 42 әріп бар:а)екі әріптен неше түрлі сөз құрауға болады,ә) мағыналы екі сөздердің кездесу ықтималдығы неге теңт болатынын есептеңіз (мағыналы екі әріпті сөздер санын Қ.Б.Бектаевтің <<Қазақ тілінің кері алфавитті сөздігі >> Алматы ,1971,кітабынан алуға болады.)

7.е,к,м,н,т,ш,ы кеспе әріптерін әбден араластырып алып:а)қатарынан тізіп қойғанда шымкент сөзінің шығу ықтималдығын анықтаңыз ,ә)үш әріптен алып тізгенде кент сөзінің шығу ықтималдығы неге тең?

8.а,а,а,а,ғ,д,қ,н,р кеспе әріптерін әбден араластырып алып ,қатарынан тізгенде қарағанда сөзінің шығу ықтималдығын анықтаңыз?

9.Класта 20оқушы бар,оның 5-еуі шахматшы.Мектепте оұу ісін меңгеруші кез келген 4 оқушыны шақырады.Келген оқушылардың:)дәл 2нің шахматшы болуы;ә)дәл 3-уінің шахматшы болуы; б)бірде біреуінің шахматшы болмау ықтималдығын анықтаңыз.

10.Дөңгелек үстелді айнала 6 адам (N адам) отырды.Белгілі бір екі адамның қатар отыру ықтималдығын анықтаңыз.

11.Цифрлы құлыптың ортақ осьті 4 дискісі бар, әрбір диск 6 бөлікке бөлінген.Бұлардың әрқайсысы бір цифрмен номерленген. Дисклер құлып корпусына қатысты белгілі бір орында тұрғанда ғана құлыптың ашылуы мүмкін,демек, цифрлар құлып `құпиясын `көрсетнтін қандай бір комбинациялар құрайды екен? Мұндағы цифрлар комбинациясын пайдаланып,құлыпты ашу ықтималдығын анықтаңыз.

12.Магазиндерге үш ревизор келген.Олардың әрқайсысы екі магазиннен тексеруге тиіс.Магазиндер ревизорларға кездейсоқ бөлінсе, бірінші ревизорға бқлінген екі магазиннің тию ықтималдығы неге тең?

13.Футбол кубогына қатынасатын 20 команда (2N команда) он-оннан (N-нан) кез келген екі топқа бөлінеді.Мынадай ықтималдықтарды есептеңіз: а)Ең күшті ең екі команда әр топқа ойнайды;ә)Ең күшті төрт команда әр топта ойнайды;б)Ең күшті екі команда бір топта ойнайды.

14.Театр залында N+R орын бар.N адам залдағы кез келген орынға отырады.Белгіленген М (М<N) орынның бос қалмау ықтималдығын анықтаңыз.

15.Телефон анықтағышынан алынған кез келген нөмір үш цифрдан құрылған.Мұның цифрларының әр түрлі болу ықтималдығы неге тең?

16.Үш монетті лақтырғанда екеуінің тиын жағымен түсу ықтималдығын анықтаңыз.

17.Жәшікте 90 жарамды, 10 жарамсыз деталь бар. Контролер кез келген 5 детальды алып тексереді:а) Алынған детальдың бәрінің де жарамды болу; ә) үшеуінің жарамды, екеуінің жарамсыз болу ықтималдығын анықтаңыз.

18.Жәшікте бірдей 10 деталь бар, олар 1,2,3,4,5,6,7,8,9,10 цифрларымен нөмірленген.Кез келген үш деталь алынды.Алынған деталь нөмірлері жай сан болу ықтималдығын анықтаңыз.

19.Қалада бір сериялы 10 000 машина бар.Үйден шыққан адамға бірінші кездескен машинаның нөмірінде 5 цифры болмау ықтималдығын анықтамыз.

20.Екі ойын кубы лақтырылды.Нөмірлерінің қосындысы жай сан болу ықтималдығын анықтаңыз.

21.Үш ойын кубы лақтырылды.Нөмірлерінің қосындысы жай сан болу ықтималдығын анықтаңыз.

№12 Оқиғалар арасындағы қатыстар мен амалдар

Осыған дейін оқиғалар арасындағы кейбір қатыстар ғана баяндалды.Ал ықтималдықтар теориясының алдына қойған негізгі мақсатының бірі жеке оқиғалар ықтималдықтары бойынша күрделі оқиғалар ықтималдықтарын анықтау болмақ.Бұл мәселені айқындау ісі қосу және көбейту теоремаларына негізделеді.Бұларды баяндаудан бұрын оқиғалар арасындағы негізгі қатыстарды келтіріп, амалдарды орындап, олардың көрнекілігін графикпен көрсетейік.

1.А және В оқиғаларының кемінде біреуінің пайда болуын сол оқиғалардың қосындысы деп атайды. Оны А+B немсесе АUВ деп белгілейді. U- бірігу (қосу) таңбасы.Сонымен, екі оқиғаның қосындысы дегенде не А оқиғасын, не В оқиғасын, не А және В екеуі де пайда болатын оқиғаны түсінеміз.Оқиғаны өзіне-өзін қосқанда сол оқиғаның өзі шығады, яғни

А+A=A

1-мысал. Оқушының жасы оқуы А оқиғасы болсын, спортшы болуы В оқиғасы болсын.Осы екі оқиғаның қосындысы С=A+B оқушы жақсы оқыса да (А оқиғасы), оқушы спортшы болса да (В оқиғасы) немесе оқушы әрі жақсы оқып,әрі спортшы болса да (А және В оқиғаларының екеуі де болса) орындалады.

2- мысал.А және В оқиғалар қосындысының геометриялық кескінін көрсету үшін кездейсоқ оқиғаны жазықтықта (жазықтық 1-чертежда көрсетілген квадрат болсын) фигура деп қарастырған қолайлы.Квадрат ішіндегі радиусы үлкен дөңгелектегі нүктелер жиыны А оқиғасының пайда болуына қолайлы жағдайларды кескіндейді, радиусы кіші дөңгелектегі нүктелер жиыны В оқиғасының пайда болуына қолайлы жағдайларды кескіндейді десек, онда А+B оқиғасы біріктірілген екі дөңгелек құрайтын облыстағы нүктелер жиынын көрсетеді.1-чертеж А және В оқиғалары үйлесімді болған жағдайдағы қосынды оқиғаны көрсетсе, 2-чертеж бұл оқиғалар үйлесімсіз болғандағы қосынды оқиғаны көрсетеді.

2.А және В оқиғаларының бірден пайда болуын олардың көбейтіндісі деп атайды.Мұны АВ немесе А В деп белгілейді. - қиылысу (көбейту) таңбасы.

АВ-ны А және В оқиғаларының пайда болуы деп оқиды.Оқиғаны өзіне - өзін көбейтсе, сол оқиғаның өзі пайда болады, яғни А*А=A.

3-мысал.Екі ойын кубы лақтырылған.Бірінші кубтың бетінде жұп ұпай (олар - 2,4,6) пайда болуы А оқиғасы болсын,екінші кубта - үшке еселік ұпай (олар - 3,6) пайда болуы В оқиғасы болады.Сона АВ екеуін де 6 ұпай пайда болу оқиғасы болады.

4-мысал.АВ оқиғасының геометриялық кескіні 3 -чертежде келтірілген екі дөңгелекке ортақ облыс болады.

3.А оқиғасы орындалып, В оқиғасы орындалмайтын оқиғаны А оқиғасы мен В оқиғасының айырмасы деп атайды.Мұны А-В немесе А\В деп белгілейді.\- азайту немесе шегеру таңбасы.

5-мысал.Кубты бір рет лақтырғанда оның жоғарғы бетінде 3-ке еселік сан шығуы А оқиғасы, үш саны шығуы В оқиғасы болсын.Сонда А-В оқиғасы 6 санының (6 ұпайдың) пайда болуын көрсетеді.Бқл мысалдағы А-B оқиғасының геометриялық кескіні 4- чертежде келтірілген А дөңгелегінің бөлігі болмақ.

4.Сынау нәтижесінде пайда болған В оқиғасы екінші бір А оқиғасының да пайда болуын қамтамасыз етсе, онда В оқиғасының пайда болуынан А оқиғасы да пайда болады дейді.Мұны В А деп белгілейді. - құрамында жату (құрамына ену) таңбасы.

6-мысал.Кубты бір рет лақтырғанда 2 ұпайдың пайда болуы В оқиғасы, жұп ұпайдың (2,4,6) ұпайдың пайда болуы В оқиғасы,жұп ұпайдың (2,4,6) пайда болуы А оқиғасы болсын.Онда В пайда болса,А да пайда болады, өйткені 2 ұпай- жұп сан.

7-мысал. В А қатысы В облысы В облысының бөлігі екенін көрсетеді.Бұл факт 5- чертежде айқын көрсетілген.Гометриялық талдаудан:

1. A A болады

2.В А және А С болса, онда В С болады.

3.В А болса,онда A + B =A және A *B=B болады.Бұларға талдау жасауды оқырмандардың өздеріне тапсырамыз.

5.Сынау нәтижесінде пайда болған А оқиғасы В оқиғасының да пайда болуын қамтыса,(яғни А В ) және осы сынауда В оқиғасының пайда болуы А оқиғасының пайда болуын қамтыса (яғни В А) , онда А және В оқиғаларын мәндес(эквивалент) деп атайды.Мұны А=B деп белгілейді.Өзара мәндес оқиғаларды бір- бірімен алмастыруға болады.Сондықтан мәндес кез келген екі оқиғаны теңбе- тең немесе тең оқиғалар деп атайды.

8-мысал.Барлық ақиқат оқиғалар мәндес, сондықтан оларды бір U әрпімен белгілеу қабылданған.Сондай ақ барлық мүмкін емес оқиғалар да мәндес,сондықтан оларды да бір V әрпімен белгілеу қабылданған.Оқиғалардың толық тобын құрайтын А,В,С .....,Z оқиғалар қосындысы - ақиқат оқиға, яғни

A+B+C+....+Z=U.

6.Оқиғалар қосындысының анықтамасы бойынша A+B оқиғасы мен B+A оқиғасы мәндес, ал көбейтіндінің анықтамасы бойнша АВ мен ВА мәндес оқиғалар.Бұл жәйт оқиғалар саны екіден артық болғанда да орындалады.Олай болса, оқиғалардың қосындысы және көбейтіндісі үшін орын ауыстыру заңы орындалады.

7.Екі үйлесімсіз А және (А емес) оқиғалары оқиғалардың толық тобын құраса, олар қарама-қарсы оқиғалар деп аталады.(6-чертежде).Олардың қосындысы - ақиқат оқиға, яғни

A+A=U (2)

ал көбейтіндісі - мүмкін емес оқиға, өйткені олардың екеуіне де ортақ оқиға болмайды, яғни

A*A=V (3)

(2) және (3) формулаларын пайдаланып, былай айтуға болады: егер екі оқиғаның қосындысы ақиқат оқиға, ал көбейтіндісі мүмкін емес оқиға болса, онда екі оқиғаны қарама - қарсы оқиғалар деп айтады.Көбейтіндісі мүмкін емес оқиға болатын қарама қарсы екі оқиғаны үйлесімсіз оқиғалар деп атайды.

9-мысал.Монетті бір рет лақтырғанда оның тиын жағынан түсуі (А оқиғасы) мен герб жағынан түсуі (А оқиғасы, яғни А емес оқиғасы) қарама-қарсы оқиғалар.

8.Оқиғалармен «не» ( А не В, А+В, АUВ), «және» (А және В, АВ, АВ), емес (А емес, А) операциялары орындалғанда шыққан нәтижелерінің де оқиға болатынын көрдік.

Бұлар оқиғаның нақты бір системасы S-пен байланысты болады.

Бұл S системасы жөнінде мынадай ұйғарымдар жасаймыз:

1.Егер S системасына А және В оқиғалары енсе, оған АВ, А+В, А-В оқиғаларыда енеді.

2. S системасына ақиқат (U) және мүмкін емес (V) оқиғалары енеді.

Осы айтылған ұйғарымдарды қанағаттандыратын оқиғалардың системасын оқиғалар өрісі деп атайды.

Жалпы айтқанда, былай: А,В,С ... оқиғаларын және жоғарыда көрсетілген амалдарды шектеулі рет қолданғанда пайда болған оқиғаларды оқиғалар өрісі деп атайды.

10-мысал. Кластан шақырылған кез келген бір оқушының белгілі бір пәнен алған бағасы жақсы болуы А оқиғасы, орташа болуы В оқиғасы, нашар (екі) болуы С оқиғасы болсын.

А+В, А+В, А+С, АВ ,АС, АС+В, А, В

оқиғаларын сипаттап беру керек.

Шешуі: А+В оқиғасы А не В оқиғалар

ының кемінде біреуінің пайда болатының көрсетеді. Сондықтан А+В оқиғасы деп оқушының жақсы немесе орташа оқитының түсінеміз. А+В оқиғасы А+В оқиғасына кері (қарама-қарсы) оқиға, ол – баланың нашар оқитындығын көрсететін С оқиғасы, яғни А+В=С. Осы сияқты, А+С=В болады. АВ оқиғасы – мүмкін емес оқиға, өйткені оқушының алған бағасы бірден жақсы да, қанағаттанарлық та болуы мүмкін емес. Осы сияқты, АС да мүмкін емес оқиға. Ал АС+В=В болатының байқау оңай.

А оқиғасына кері оқиға (А) оқушының орташа (В) не нашар (С) оқуын сипаттайды, демек, А=В+С. Ал А=В+С және В+С=А болатындығынаң А=А болатыны түсінікті. Осы сияқты, В=В болатынын сипаттап беру қиын емес.