Определим ачх и фчх фильтра

,

где

Функция A(θ) однородного фильтра 2-го порядка при M=1/3

АЧХ однородного фильтра 2-го порядка при M=1/3

ФЧХ однородного фильтра 2-го порядка

Поскольку ФЧХ принято представлять в интервале значений фазы от –π до π, то соотношение для корректируется путем прибавления или вычитания 2 π

2.8. Триангулярный фильтр

Последовательное соединение двух одинаковых однородных фильтров порядка N образует триангулярный фильтр порядка 2N.

Последовательное соединение двух однородных фильтров 2-го порядка

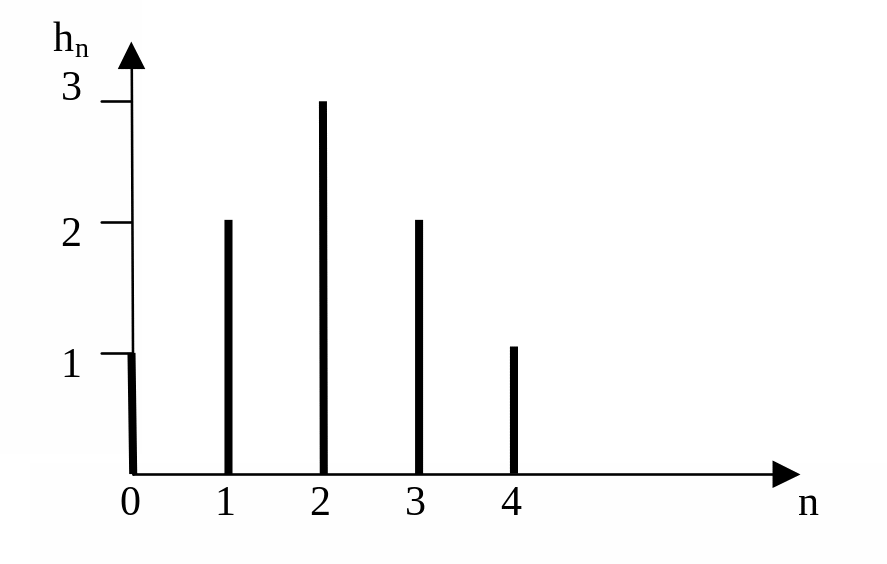
Импульсная характеристика

Триангулярный фильтр 4-го порядка

2.9.Устойчивость цифровых фильтров

Критерии устойчивости цифровых фильтров:

1.Критерий «ОВ-ОВ» («Ограниченный вход – ограниченный выход»)

Цифровой фильтр устойчив, если при ограниченном входном сигнале выходной сигнал фильтра также ограничен.

Условие ограниченности входного сигнала определяется соотношением

Условием ограниченности выходного сигнала является

.

2. Критерий оценки устойчивости по импульсной характеристике фильтра

Выходной сигнал фильтра представляет собой дискретную свертку входного сигнала и импульсной характеристики фильтра

.

Абсолютное значение n-го отсчёта выходного сигнала удовлетворяет неравенству

.

При справедливо неравенство

.

Следовательно,

.

Таким образом, чтобы обеспечить выполнение условия , достаточно выполнить условие

.

Цифровой фильтр устойчив, если сумма абсолютных значений отсчетов его импульсной характеристики конечна.

Из этого критерия следует, что все фильтры с конечной импульсной характеристикой абсолютно устойчивы.

Пример:

,

где – положительная константа, от которой зависит скорость убывания отсчетов импульсной характеристики.

Учитывая, что , получим

.

3.Критерий оценки устойчивости по системной функции фильтра

.

Модуль системной функции удовлетворяет неравенству

.

При справедливо неравенство

.

При и при .

Последнее соотношение означает, что в устойчивом цифровом фильтре должны отсутствовать полюсы системной функции в области комплексной переменной z, которая удовлетворяет неравенству

Следовательно, если полюсы существуют, то в устойчивом фильтре они должны располагаться в области комплексной переменной z, для которой выполняется условие

Цифровой фильтр устойчив, если полюсы системной функции располагаются внутри круга единичного радиуса с центром в начале координат .

Пример 1:

На рисунке 1 дано графическое представление алгоритма функционирования цифрового фильтра. Коэффициенты системной функции равны: A = 0.5 ,

B = -1, C = -1.4.

Сделайте заключение об устойчивости фильтра

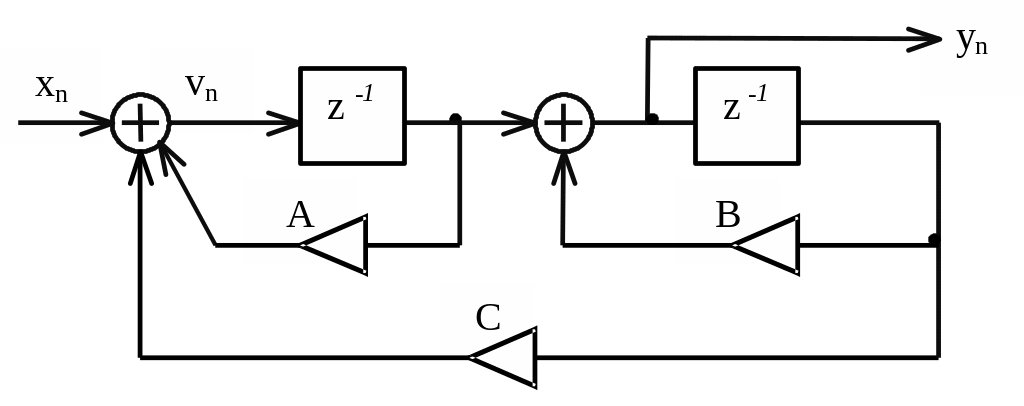
Рисунок 1

1. Из рисунка видно,что

Из первого уравнения

Подставим V(z) во второе уравнение

Из последнего соотношения получим

Системная функция цифрового фильтра определяется соотношением

Определим полюсы системной функции. Приравняв знаменатель системной функции к нулю, получим квадратное уравнение для определения ее полюсов

Подставляя в него значения A, B и C, получим

.

Корни уравнения равны

.

Следовательно, фильтр устойчив.

Пример 2:

Сделайте обоснованное заключение об устойчивости цифрового фильтра рисунка 1, если A₁₁ = 0.1, A₂₁= 0.9, A₁₂ = - 0.1, A₂₂ =1.1.

Цифровой фильтр выполнен в виде последовательного соединения двух звеньев второго порядка.

Системная функция фильтра определяется соотношением

,

где

.

Проверяем устойчивость каждого звена.

Звено №1

или

.

Следовательно, первое звено устойчиво.