Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Вятский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

методичка электротех.doc

Скачиваний:

Добавлен:

01.07.2025

Размер:

3.29 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

Задания для контрольной работы № 1

Задача № 1

Цепь постоянного тока содержит несколько резисторов, соединенных смешанно. Схема цепи приведена на соответствующем рисунке. Номер рисунка, значения сопротивлений резистора; тока или напряжения приведены в таблице 1. Например, через резистор R₃ проходит ток I₃, действует напряжение U₃.

Определите величины отмеченные «х» и составьте баланс мощности цепи.

Рисунок 1 Рисунок 2

Рисунок 3 Рисунок 4

Рисунок 5

Таблица 1

№ вари-антов	№ рис.	R₁	R₂	R₃	R₄	R₅	R₆	I₁	I₂	I₃	I₄	I₅	I₆	U₁	U₂	U₃	U₄	U₅	U₆	U_AB
01	1	2	4	12	3	6	-	x	x	x	x	x	-	x	x	x	x	x	-	100
02	1	2	4	12	3	6	-	20	x	x	x	x	-	x	x	x	x	x	-	x
03	1	2	4	12	3	6	-	x	x	x	x	x	-	x	30	x	x	x	-	x
04	1	2	4	12	3	6	-	x	x	x	x	10	-	x	x	x	x	x	-	x
05	1	2	4	12	3	6	-	x	3,75	x	x	x	-	x	x	x	x	x	-	x
06	1	2	4	12	3	6	-	x	x	x	5	x	-	x	x	x	x	x	-	x
07	1	2	4	12	3	6	-	x	x	x	x	x	-	x	x	x	x	30	-	x
08	1	2	4	12	3	6	-	x	x	1,25	x	x	-	x	x	x	x	x	-	x
09	1	2	4	12	3	6	-	x	x	x	x	x	-	20	x	x	x	x	-	x
10	1	2	4	12	3	6	-	x	x	x	12	x	-	x	x	x	x	x	-	x
11	2	4	2	6	4	10	2	x	x	x	x	x	x	x	x	x	x	x	x	50
12	2	4	2	6	4	10	2	5	x	x	x	x	x	x	x	x	x	x	x	x
13	2	4	2	6	4	10	2	x	2	x	x	x	x	x	x	x	x	x	x	x
14	2	4	2	6	4	10	2	x	x	1,2	x	x	x	x	x	x	x	x	x	x
15	2	4	2	6	4	10	2	x	x	x	2	x	x	x	x	x	x	x	x	x
16	2	4	2	6	4	10	2	x	x	x	x	x	x	x	x	x	x	18	x	x
17	2	4	2	6	4	10	2	x	x	x	x	x	x	x	x	x	10	x	x	x
18	2	4	2	6	4	10	2	x	x	x	x	x	x	x	x	20	x	x	x	x
19	2	4	2	6	4	10	2	x	x	x	x	x	x	x	30	x	x	x	x	x
20	2	4	2	6	4	10	2	x	x	x	x	x	x	20	x	x	x	x	x	x
21	3	10	15	10	5	10	4	x	x	x	x	x	x	x	x	x	x	x	x	120
22	3	4	15	10	5	10	4	x	x	x	x	x	x	x	x	x	x	x	16	x
23	3	4	15	10	5	10	4	x	x	x	x	x	x	x	x	x	x	30	x	x
24	3	4	15	10	5	10	4	x	x	x	x	x	x	x	x	x	10	x	x	x
25	3	4	15	10	5	10	4	x	x	x	x	x	x	x	x	30	x	x	x	x
26	3	4	15	10	5	10	4	x	x	x	x	x	4	x	x	x	x	x	x	x
27	3	4	15	10	5	10	4	x	x	x	3	x	x	x	x	x	x	x	x	x
28	3	4	15	10	5	10	4	x	x	x	x	x	x	x	60	x	x	x	x	x
29	3	4	15	10	5	10	4	x	x	x	x	x	x	40	x	x	x	x	x	x
30	3	4	15	10	5	10	4	12	x	x	x	x	x	x	x	x	x	x	x	x
31	4	4	10	4	10	15	6	10	x	x	x	x	x	x	x	x	x	x	x	x
32	4	4	x	6	2	3	4,8	x	15	x	x	x	x	x	60	x	x	x	x	x
33	4	4	10	4	10	15	5	x	x	x	x	x	x	x	120	x	x	x	x	x
34	4	4	10	5	15	10	4	x	x	x	x	x	x	x	x	x	x	x	x	250
35	4	9	10	5	15	10	4	x	x	x	x	x	8	x	x	x	x	x	x	x
36	4	6	15	12	4	12	5	x	x	x	x	x	x	200	x	x	x	x	x	x
37	4	4	15	4	12	4	3	x	x	x	x	x	x	x	x	x	48	x	x	x
38	4	4	10	10	15	10	4	x	x	x	x	6	x	x	x	x	x	x	x	x
39	4	8	10	4	10	15	10	20	x	x	x	x	x	x	x	x	x	x	x	x
40	4	8	10	4	10	15	10	x	x	20	x	x	x	x	x	x	x	x	x	x
41	5	3	6	6	3	12	4	x	4	x	x	x	x	x	x	x	x	x	x	x
42	5	3	6	6	3	12	4	x	x	4	x	x	x	x	x	x	x	x	x	x
43	5	3	6	6	3	12	4	x	x	x	6	x	x	x	x	x	x	x	x	x
44	5	3	6	6	3	12	4	x	x	x	x	x	x	x	x	x	x	x	12	x
45	5	3	6	6	3	12	4	x	x	x	x	x	x	x	x	24	x	x	x	x
46	5	3	6	6	3	12	4	x	x	x	x	1	x	x	x	x	x	x	x	x
47	5	3	6	6	3	12	4	x	x	x	x	x	x	x	x	x	12	x	x	x
48	5	3	6	6	3	12	4	x	x	x	x	x	4,5	x	x	x	x	x	x	x
49	5	3	6	6	3	12	4	x	x	x	x	x	x	x	x	x	x	24	x	x
50	5	3	6	6	3	12	4	x	x	x	x	x	x	x	x	x	x	x	x	90

Методические указания к задаче 1

Пример

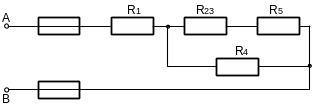
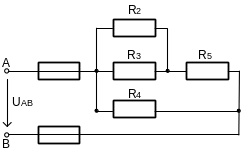
Для схемы, приведенной на рисунке 1.1а, определите эквивалентное сопротивление цепи R_AB_,токи в каждом резисторе и напряжение U_AB, приложенное к цепи. Заданы сопротивления резисторов и ток I₄ в резисторе R₄. Как изменятся токи в резисторах при: а) замыкание рубильника Р; б) расплавление вставки предохранителя Пр4? В обоих случаях напряжение U_ABостается неизменным.

Решение. Задача относится к теме «Электрические цепи постоянного тока». Предварительно обозначаем стрелкой направление тока в каждом резисторе, индекс тока должен соответствовать номеру резистора, через который он проходит.

1. Определяем общее сопротивление разветвления R_2,R₃. Резисторы соединены параллельно, поэтому:

Ом

Теперь схема цепи принимает вид, показанный на рисунке 1.1б.

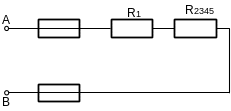
2. Резисторы R_{2, 3} и R₅ соединены последовательно, их общее сопротивление:

3. Резисторы и R₄ соединены параллельно, их общее сопротивление:

Теперь схема цепи имеет вид, приведенный на рисунке 1.1г.

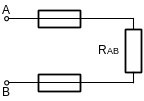
4. Находим эквивалентное сопротивление всей цепи:

(рисунок 1.1д).

5. Зная силу тока I₄, находим напряжение на резисторе R₄:

Это же напряжение приложено к резисторам R_2,3 + R₅ (рисунок 1.1б).

Поэтому ток в резисторе R₅:

6. Находим падение напряжения на резисторе R₅:

поэтому напряжение на резисторах R_2,3:

7. Определяем токи в резисторах R₂и R₃:

Применяя 1 закон Кирхгофа, находим ток в резисторе R₁:

8. Вычисляем падение напряжения на резисторе R₁:

9. Находим напряжение U_AB, приложенное ко всей цепи:

или

10. При включении рубильника P₁, сопротивление R₁замыкается накоротко, и схема цепи имеет вид на рисунке 1.1е. Эквивалентное сопротивление цепи в этом случае: R_AB=R_2,3,4,5=5 Ом.

Поскольку напряжение U_AB остается равным 100 В, можно найти токи в резисторах R₄ и R₅:

;

Определим падение напряжения на резисторе R₅:

Поэтому напряжение на резисторах R₂и R₃:

Теперь найдем токи в резисторах R₂и R₃:

; .

Проверим правильность вычисления токов, используя 1 закон Кирхгофа: , однако .

Задача решена верно.

11. При расплавлении предохранителя Пр4 резистор R₄ выключается и схема принимает вид на рисунке 1.1ж.

Вычисляем эквивалентное сопротивление схемы:

Поскольку напряжение U_AB остается неизменным, находим токи I₁, I₅:

Напряжение на резисторах R_2,R₃:

Находим токи I₂, I₃:

; .

Сумма этих токов равна току I₁:

12. Баланс мощности:

1000 Вт=1000 Вт

а) б)

в) г)

д) е)

ж)

Рисунок 1.1

Задача № 2

Цепь переменного тока содержит различные элементы (резисторы, индуктивности, емкости), включенные последовательно. Схема цепи приведена на соответствующем рисунке. Номер рисунка и значение сопротивлений всех элементов, а также один дополнительный параметр заданы в таблице 2.

Начертите схему цепи и определите следующие величины, относящиеся к данной цепи, если они не заданы в таблице 2:

1) полное сопротивление Z; 2) напряжение U, приложенное к цепи; 3) ток I; 4) угол сдвига фаз (по величине и по признаку); 5) активную P, реактивную Q, полную S мощности цепи

Начертите в масштабе векторную диаграмму цепи и поясните ее построение.

Ответьте на вопрос: как изменятся активная, реактивная и полная мощности цепи при увеличении частоты тока в 2 раза и при неизменном приложенном напряжении? (Поясните!)

Рисунок 6 Рисунок 7

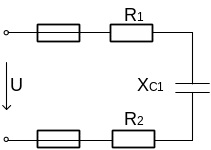
Рисунок 8 Рисунок 9

Рисунок 10

Таблица 2

Номера вариантов	Номер рисунка	R_1,Ом	R₂_,Ом	X_L1,Ом	X_L2,Ом	X_C1,Ом	X_C2,Ом	Дополнительный параметр
01	6	4	-	6	-	3	-	Q_L1=150 вар
02	7	6	2	3	-	9	-	U=40 B
03	8	10	6	-	-	12	-	I=5 A
04	9	6	2	6	-	-	-	P_R1=150 Вт
05	10	8	-	3	-	3	6	S=360 ВА
06	6	3	-	2	-	6	-	U=50 B
07	7	4	4	4	-	10	-	I=4 A
08	8	4	2	-	-	8	-	Q_L1=80 вар
09	9	8	4	16	-	-	-	S=250 ВА
10	10	6	-	8	-	4	12	P=150 Вт
11	6	6	-	10	-	2	-	I=5 A
12	7	4	2	12	-	4	-	P=24 Вт
13	8	5	3	-	-	6	-	S=250 ВА
14	9	3	1	3	-	-	-	Q_L1=80 вар
15	10	4	-	10	-	2	5	Q=300 вар
16	6	8	-	4	-	10	-	P=800 Вт
17	7	3	3	2	-	10	-	Q_С₁= -160 вар
18	8	8	4	-	-	16	-	U_R1=32 B
19	9	10	6	12	-	-	-	U=100 B
20	10	6	-	4	-	8	4	I=4 A
21	6	12	-	18	-	2	-	S=500 ВА
22	7	8	4	20	-	4	-	Q_L1=500 вар
23	8	2	2	-	-	3	-	P=100 Вт
24	9	4	4	6	-	-	-	I=2 A
25	10	12	-	12	-	20	8	U=60 B
26	6	4	-	6	-	3	-	U_L1=30 B
27	7	10	6	16	-	4	-	U=100 B
28	8	25	7	-	-	24	-	P₂=28 Вт
29	9	10	6	12	-	-	-	Q=48 вар
30	10	30	-	70	-	10	20	S=200 ВА
31	6	3	-	2	-	6	-	U_C1= -36 B
32	7	7	5	4	-	20	-	U_R2=25 B
33	8	6	10	-	-	12	-	Q_C1= -1200 вар
34	9	14	18	24	-	-	-	I=3 A
35	10	12	-	10	-	3	2	P=432 Вт
36	6	6	-	10	-	2	-	Q_C1= -50 вар
37	7	30	10	50	-	20	-	P₂=40 Вт
38	8	4	4	-	-	6	-	U_R1=40 B
39	9	5	7	5	-	-	-	I=4 A
40	10	5	-	20	-	3	5	Q_L1=1280 вар
41	6	12	-	15	-	10	-	I=10 A
42	7	10	6	10	-	22	-	U_C1= 44 B
43	8	6	6	-	-	9	-	U_R1=42 B
44	9	20	24	33	-	-	-	P_R1=500 Bт
45	10	28	-	30	-	25	26	U=350 B
46	6	5	-	20	-	8	-	U=260 B
47	7	3	9	3	-	15	-	Q_L1=45 вар
48	8	4	5	-	-	12	-	P_R2=720 Bт
49	9	10	5	20	-	-	-	U_L1=150 B
50	10	27	-	36	-	22	50	Q_C2= -200 вар

Методические указания к решению задачи 2

Пример

Активное сопротивление катушки R_К=6 Ом, индуктивное X_L=10 Ом. Последовательно с катушкой включены активное сопротивление R=2 Ом и конденсатор сопротивлением X_C=4 Ом (рисунок 2.1а). К цепи приложено напряжение U=50 В (действующее значение). Определите:

1) полное сопротивление цепи;

2) ток;

3) коэффициент мощности;

4) активную, реактивную и полную мощности;

5) напряжение на каждом сопротивлении.

Начертите в масштабе векторную диаграмму цепи.

Решение.

1. Определяем полное сопротивление цепи:

2. Определяем ток:

3. Определяем коэффициент мощности цепи:

по таблицам Брадиса, находим .

Угол сдвига фаз по косинусу, во избежание потери знака угла (косинус является четной функцией).

4. Определяем активную мощность цепи:

5. Определяем реактивную мощность цепи:

6. Определяем полную мощность цепи:

или .

7. Определяем падения всех напряжений на сопротивлении цепи:

; ; ; .

Построение векторной диаграммы начинаем с выбора масштаба для тока и напряжения. Задаемся масштабом по току: 1 см = 1,0 А и масштабом по напряжению: 1 см = 10 В. Построение векторной диаграммы (рисунок 2.1б) начинаем с вектора тока, который откладываем по горизонтали в масштабе .

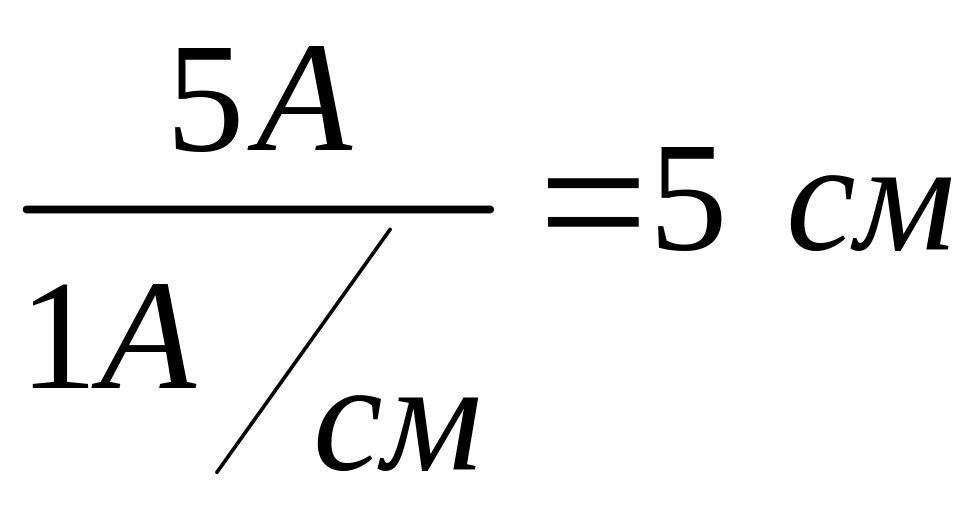Вдоль вектора тока откладываем векторы падения напряжения на активных сопротивлениях U_RK и U_R: ; 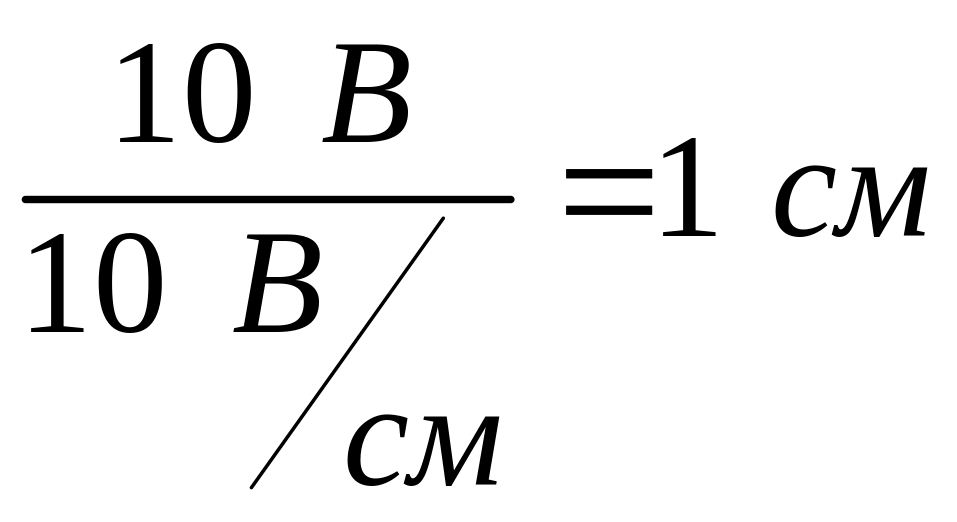. Из конца вектора U_Rоткладываем в сторону опережения вектора тока на вектор падения напряжения U_Lна индуктивном сопротивлении длиной 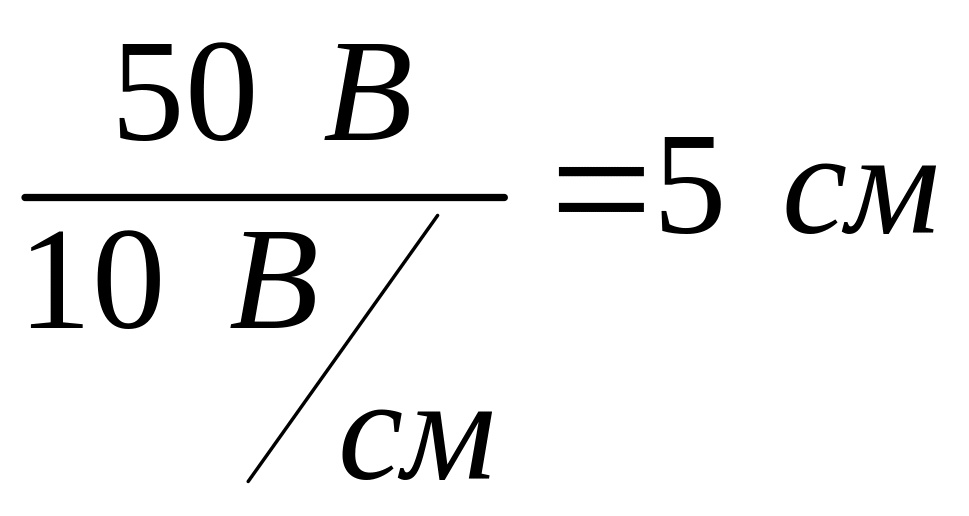. Из конца вектора U_L откладываем в сторону отставания от вектора тока на вектор падения напряжения на конденсаторе U_C длиной . Геометрическая сумма векторов U_RK, U_R, U_L, U_Cравна полному напряжению U, приложенному к цепи.

а) б)

Рисунок 2.1

Задача № 3

Разветвленная цепь переменного тока состоит из двух параллельных ветвей, содержащих активные сопротивления, индуктивности и емкости. Схема приведена на соответствующем рисунке.

Начертите схему цепи и определите величины, отмеченные в таблице 3 крестиками. Постройте векторную диаграмму цепи. Индекс «1» означает, что величина относится к первой ветви, индекс «2» - ко второй.

I₁ и I₂ – токи в ветвях, I – ток в неразветвленной части цепи; U- напряжение, приложенное к цепи; P – активная, Q – реактивная, S – полная мощность всей цепи.

Каким образом в заданной цепи можно уменьшить ток неразветвленной части, при неизменном приложенном напряжении.

Рисунок 11 Рисунок 12 Рисунок 13

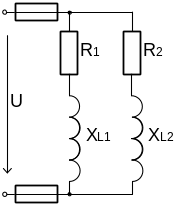
Рисунок 14 Рисунок 15 Рисунок 16

Рисунок 17 Рисунок 18

Рисунок 19 Рисунок 20

Номера вариантов	Номер рисунка	R₁, Ом	R₂, Ом	X_L1, Ом	X_L2, Ом	X_C1, Ом	X_C2, Ом	U, В	I, А	I₁, А	I₂, А	P, Вт	Q, Вар	S, ВА	P₁, Вт	P₂, Вт	Q₁, вар	Q₂, вар
01	11	5		-	4	-	-	x	x	x	x	x	x	x	100	x	-	x
02	12	10	8	-	-	-	6	20	x	x	x	x	x	x	x	x	x	x
03	13	4	-	-	-	-	5	x	x	5	x	x	x	x	x	x	x	x
04	14	4	6	3	8	-	-	x	x	x	4	x	x	x	x	x	x	x
05	15	16	-	12	-	-	10	80	x	x	x	256	x	x	x	x	x	x
06	16	24	16	-	12	32	-	x	x	x	x	x	x	x	x	x	x	x
07	17	5	4	-	6	-	-	x	x	x	6	x	x	x	x	x	x	x
08	18	15	12	-	20	-	4	100	x	x	x	x	x	x	240	x	x	x
09	19	8	16	-	-	6	12	x	x	x	x	x	x	x	x	x	x	x
10	20	4	8	-	12	3	6	50	x	x	x	x	x	x	x	288	x	x
11	11	10	6	-	8	-	-	x	x	x	x	x	x	x	x	x	x	x
12	12	2	3	-	-	-	4	x	x	5	x	x	x	x	x	x	x	x
13	13	12	-	-	-	-	8	x	x	x	6	x	x	x	x	x	x	x
14	14	6	3	8	4	-	-	120	x	x	x	x	x	x	x	300	x	x
15	15	32	-	24	-	-	40	x	x	x	x	x	x	x	x	x	x	x
16	16	12	8	-	10	16	-	x	x	x	x	x	x	x	x	x	x	250
17	17	2	2	-	3	-	-	30	x	x	x	x	x	x	x	16	x	x
18	18	5	8	-	4	-	10	x	x	x	x	x	x	x	x	x	x	x
19	19	3	6	-	-	4	8	20	x	x	4	x	x	x	x	x	x	x
20	20	8	4	-	5	6	8	x	x	x	x	x	x	x	x	x	x	x
21	11	4	4	-	3	-	-	x	x	x	8	x	x	x	x	x	x	x
22	12	5	4	-	-	-	3	8	x	x	2	x	x	x	x	x	x	x
23	13	2	-	-	-	-	4	x	x	x	x	x	x	x	x	x	x	x
24	14	8	12	6	16	-	-	x	x	x	x	x	x	x	x	x	x	144
25	15	48	-	64	-	-	60	x	x	3	x	x	x	x	x	x	x	x
26	16	3	8	-	6	4	-	x	x	5	x	x	x	x	x	x	x	x
27	17	6	3	-	8	-	-	x	x	x	x	x	72	x	x	x	x	x
28	18	10	6	-	12	-	4	x	x	x	x	x	32	x	x	x	x	x
29	19	24	12	-	-	32	16	120	x	x	x	x	x	x	x	x	x	x
30	20	64	24	-	40	48	8	x	x	x	x	x	x	x	64	x	x	x
31	11	8	4	-	3	-	-	x	x	5	x	x	x	x	x	x	x	x
32	12	12	6	-	-	-	8	x	x	x	x	x	-288	x	x	x	x	x
33	13	3	-	-	-	-	4	x	x	x	x	48	x	x	x	x	x	x
34	14	16	3	12	4	-	-	40	x	x	x	x	x	x	x	x	x	x
35	15	8	-	6	-	-	8	x	x	x	5	x	x	x	x	x	x	x
36	16	32	16	-	12	24	-	x	x	x	6	x	x	x	x	x	x	x
37	17	5	2	-	3	-	-	20	x	x	x	x	x	x	x	x	x	x
38	18	20	32	-	30	-	6	x	x	x	x	x	x	x	x	128	x	x
39	19	16	6	-	-	12	8	x	x	x	x	x	x	x	64	x	x	x
40	20	6	8	-	4	8	10	x	x	5	x	x	x	x	x	x	x	x
41	11	8	4	-	3	-	-	x	x	x	x	x	x	x	x	256	x	x
42	12	3	3	-	-	-	4	x	x	x	x	x	x	x	x	x	x	-48
43	13	5	-	-	-	-	10	x	x	x	x	x	-40	x	x	x	x	x
44	14	24	12	32	16	-	-	x	x	2	x	x	x	x	x	x	x	x
45	15	6	-	8	-	-	12	x	x	x	x	x	x	x	x	x	288	x
46	16	4	6	-	8	3	-	x	x	x	x	x	x	x	256	x	x	x
47	17	9	4	-	6	-	-	x	x	10	x	x	x	x	x	x	x	x
48	18	5	8	-	4	-	10	60	x	x	x	x	x	x	x	x	x	x
49	19	64	24	-	-	48	32	x	x	x	x	x	x	x	x	384	x	x
50	20	3	6	-	10	4	2	x	x	x	3	x	x	x	x	x	x	x

Методические указания к решению задачи 3

Пример

Катушка с активным сопротивлением R₁=6 Ом и индуктивным X_L₁=8 Ом соединена параллельно с конденсатором, емкостное сопротивление которого X_C₂=10 Ом. Определите:

1. токи в ветвях и в неразветвленной части цепи;

2. активные и реактивные мощности ветвей и всей цепи;

3. полную мощность цепи;

4. углы сдвига фаз между током и напряжением в каждой ветви и во всей цепи.

Начертите в масштабе векторную диаграмму цепи. К цепи приложено напряжение U=100 В (схема рисунок 3.1а).

Решение.

1. Определяем токи в ветвях:

; .

2. Углы сдвига фаз в ветвях находим по синусам углов:

; .

Так как , то напряжение опережает ток,

; , т.е. напряжение отстает от тока, так как . По таблицам Брадиса находим ; .

3. Определяем активные и реактивные составляющие токов в ветвях:

; ; ; .

4. Определяем ток в неразветвленной части цепи:

5. Определяем коэффициент мощности всей цепи:

6. Определяем активные и реактивные мощности ветвей и всей цепи:

; ; ;

; .

7. Определяем полную мощность цепи и напряжение:

Ток в неразветвленной части цепи можно определить значительно проще, без разложения токов на составляющие, зная полную мощность цепи и напряжение.

б)

а)

Рисунок 3.1

8. Для построения векторной диаграммы задаемся масштабом по току: 1 см=2,5 А и масштабом по напряжению: 1 см=25 В.

Построение начинаем с вектора напряжения U (рисунок 3.1б) под углом к нему (в сторону отставания) откладываем в масштабе вектор тока I₁, под углом (в сторону опережения) – вектор тока I₂. Геометрическая сумма токов I₁и I₂ равна току в неразветвленной части I. На векторной диаграмме показаны также проекции векторов токов на вектор напряжения (активная составляющая I_A₁) и вектор перпендикулярный ему (реактивные составляющие I_P₁и I_P₂). При отсутствии конденсатора реактивная мощность первой ветви не компенсировалась бы, и ток увеличивался бы до I=I₁=10 А.

Задача № 4

Три группы сопротивлений, соединенных звездой с нулевым проводом включены в трехфазную сеть переменного тока с линейным напряжением U. Активное сопротивление в фазах A, B и C соответственно равны R_A, R_B, R_C, реактивные X _A, X_B, X_C. Характер реактивных сопротивлений (индуктивное или емкостное) указан в схеме цепи. Угол сдвига фаз в каждой фазе равны I_A, I_B, I_C, ток в нулевом проводе в нормальном режиме I₀. Фазы нагрузки потребляют активные мощности P_A, P_B, P_C и реактивные мощности Q_A, Q_B, Q_C. В таблице вариантов указано, в каком аварийном режиме находится цепь.

Начертите схему цепи для своего варианта, таблица 4; определите величины, отмеченные крестиками в таблице вариантов; начертите в масштабе векторные диаграммы для нормального и аварийного режимов. Ток в нулевом проводе определите графически из векторной диаграммы.

При вычислениях примите: ; ; ; .

Рисунок 21 Рисунок 22

Рисунок 23

Таблица 4.

Вариант

Схема цепи, рис.

U, B

104

660

380

692

208

R_A, Ом

R_B, Ом

R_C, Ом

X_A, Ом

X_B, Ом

X_C, Ом

36⁰50’

53⁰10’

36⁰50’

53⁰10’

I₀, A

I_A, A

I_B, A

I_C, A

2,4

P_A, Вт

2904

6400

P_B, Вт

576

8670

P_C, Вт

216

23120

1936

3840

Q_A, вар

240

36100

3872

Q_B, вар

432

11550

1100

4000

1200

Q_C, вар

288

17340

1452

В аварийном режиме произошел обрыв фазы

Вариант

Схема цепи, рис.

U, B

208

380

660

104

660

104

R_A, Ом

R_B, Ом

R_C, Ом

X_A, Ом

X_B, Ом

X_C, Ом

36⁰50’

53⁰10’

36⁰50’

53⁰10’

36⁰50’

53⁰10’

I₀, A

I_A, A

I_B, A

I_C, A

2,4

P_A, Вт

6400

P_B, Вт

8670

576

8670

P_C, Вт

216

23120

Q_A, вар

4800

1728

3872

36100

240

36100

240

Q_B, вар

1200

11550

432

11550

Q_C, вар

5120

230,4

1452

17340

288

17340

288

В аварийном режиме произошел обрыв фазы

Методические указания к решению задачи 4

Пример

Для схемы, приведенной на рисунке 4.1, постройте в масштабе векторную диаграмму и определите графически ток в нулевом проводе. Как изменится ток в нулевом проводе при отключении линейного провода B? Линейное напряжение U=380 В.

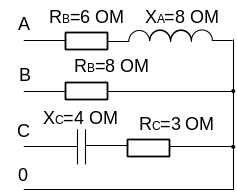
Рисунок 4.1

Решение

1. Полные сопротивления фаз:

;

2. Фазные (они же линейные) токи:

; ; .

3. Угол сдвига фаз между фазным током и напряжением в каждой фазе:

, (отстающий);

, ;

, (опережающий).

4. Построение векторной диаграммы начинаем с фазных напряжений U_A, U_B, U_C, располагая их под углом 120⁰ относительно друг друга. Чередование фаз принято обычным: за фазой A – фаза B, за фазой B – фаза C (в положительном направлении). Под углом _A, _B, _C к соответствующим векторам фазных напряжений откладываем векторы линейных токов I_A, I_B, I_C, геометрическая сумма последних равна току в нулевом проводе I₀, ток в фазе A отстает от напряжения U_Aна угол _A=53⁰; ток в фазе B совпадает с напряжением U_B; ток в фазе C опережает напряжение U_C на угол _C=37⁰ (смотрите рисунок 4.1а). Из векторной диаграммы находим I₀=50 А.

5. При отключении линейного провода B, линейный ток I_B=0, а токи I_A и I_C не меняют своей величины. Ток в нулевом проводе, в этом случае, равен геометрической сумме токов I_A и I_Cиз диаграммы находим I₀=28 А.

Рисунок 4.1 а

Задача № 5

Три группы сопротивлений соединены в треугольник и включены в трехфазную сеть переменного тока с линейным направлением U. Активные сопротивления в фазах AB, BC, CA соответственно равны R_AB_,R_BC, R_CA; реактивные – X_AB, X_BC, X_CA (характер реактивных сопротивлений (индуктивное или емкостное) указан на схеме цепи). Углы сдвига фаз в каждой фазе равны _AB, _BC, _CA. В фазах нагрузки в нормальном режиме протекают токи I_AB, I_BC, I_CA; линейные токи в нормальном режиме равны I_A, I_B, I_C. Трехфазная цепь потребляют активную мощность P, реактивную Q, полную S.

Начертите схему цепи для своего варианта, определите величины, отмеченные крестиками в таблице 5, и начертите в масштабе векторные диаграммы цепи для нормального и аварийного режимов. Линейные токи в нормальном и аварийном режимах определите из векторных диаграмм, рисунки 24-25.

Рисунок 24 Рисунок 25

Таблица 5

Вариант	31	32	33	34	35	36	37	38	39	40
Схема цепи, рис.	24	24	24	24	24	24	24	24	24	24
R_AB,Ом	6	x	4	3	4	4	x	x	x	x
R_BC,Ом	-	-	-	-	-	-	-	-	-	-
R_CA,Ом	10	5	3	4	x	x	38	x	5	x
X_AB,Ом	x	x	x	4	x	3	12	x	3	x
X_BC,Ом	5	5	3	10	x	5	4	x	8	5
X_CA,Ом	-	-	-	-	-	-	-	-	-	-
_AB	53⁰10’	x	x	x	36⁰50’	x	36⁰50’	x	36⁰50’	x
_BC	x	x	x	x	x	x	x	x	x	x
_CA	x	x	x	x	x	x	x	x	x	x
I_AB, A	x	40	40	x	x	x	19	x	x	40
I_BC, A	44	x	x	x	x	40	x	40	x	x
I_CA, A	x	x	x	x	x	x	x	40	40	x
I_A, A	x	x	x	x	x	x	x	x	x	x
I_B, Вт	x	x	x	x	x	x	x	x	x	x
I_C, Вт	x	x	x	x	x	x	x	x	x	x
P, Вт	x	14400	x	x	14400	14400	x	14400	x	x
Q, вар	x	x	3200	x	3200	x	x	x	x	3200
S, ВА	x	x	14770	x	x	x	x	14770	14770	x
U, B	x	200	x	220	200	x	x	200	x	200
В аварийном режиме произошел обрыв фазы	Линей ного провода А	Фазы АВ	Линейного провода В	Фазы ВС	Линейного провода С	Фазы СА	Фаз АВ и СА	Фаз АВ и ВС	Фаз ВС и СА	Фазы СА

Вариант	41	42	43	44	45	46	47	48	49	50
Схема цепи, рис.	25	25	25	25	25	25	25	25	25	25
R_AB,Ом	-	-	-	-	-	-	-	-	-	-
R_BC,Ом	4	x	4	x	x	15	x	x	x	4
R_CA,Ом	12	12	x	12	x	x	6	x	8	6
X_AB,Ом	10	10	10	x	x	20	x	20	x	12
X_BC,Ом	3	x	x	3	x	x	3	x	20	x
X_CA,Ом	16	x	x	x	x	6	8	x	6	x
_AB	x	x	x	x	x	x	x	x	x
_BC	x	x	36⁰50’	x	36⁰50’	53⁰10’	36⁰50’	x	53⁰10’	36⁰50’
_CA	x	53⁰10’	53⁰10’	x	53⁰10’	36⁰50’	x	36⁰50’	x	x
I_AB, A	x	x	x	40	x	x	5	x	25	x
I_BC, A	x	x	80	80	80	x	x	x	20	x
I_CA, A	x	20	x	20	20	x	6	8	x	6
I_A, A	x	x	x	x	x	x	x	x	x	x
I_B, Вт	x	x	x	x	x	x	x	x	x	x
I_C, Вт	x	x	x	x	x	x	x	x	x	x
P, Вт	x	30400	x	x	x	x	x	384	x	792
Q, вар	x	15800	15800	x	x	x	x	16	x	x
S, ВА	x	x	x	x	34250	x	x	x	x	x
U, B	400	x	x	400	400	500	x	400	x	x
В аварийном режиме произошел обрыв фазы	Фазы АВ	Линейного провода В	Фазы СА	Линейно го провода A	Фаз ВС и СА	Фазы ВС	Линейно го провода C	Фаз АВ и СA	Фаз AВ и BС	Фазы АB

Рисунок 5.1

Методические указания к решению задачи 5

Пример

Для схемы, приведенной на рисунке 5.1, построить в масштабе векторную диаграмму. Как изменятся линейные токи при отключении фазы CA? Постройте для этого случая векторную диаграмму. Линейное напряжение сети U=220 В.

Рисунок 5.1

Решение

1. Фазные токи:

; ; .

2. Угол сдвига фаз:

(опережающий);

(отстающий).

3. Построение векторной диаграммы начинаем с фазных напряжений (они же линейные). Откладываем напряжения U_AB_,U_BC_,U_CA_, располагая их под углом 120⁰ относительно друг друга. Под углом к соответствующим векторам фазных напряжений откладываем фазные токи I_AB_,I_BC_,I_CA. Ток в фазе АВ совпадает с напряжение U_AB; ток в фазе ВС опережает напряжение U_BC на 90⁰; ток в фазе СА отстает от напряжения U_CA на угол 53⁰. Затем строим векторы линейных токов на основании уравнений: I_A=I_AB-I_CA; I_B=I_BC-I_CA; I_C=I_CA-I_BC.

Линейные токи находим из векторной диаграммы – измерением: I_A=41 А, I_B=37 А, I_C=73 А. Эти токи можно определить аналитически, пользуясь теоремой косинусов.

а)

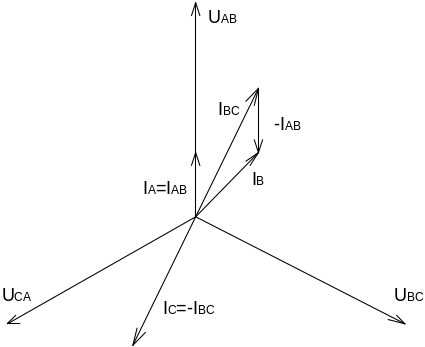
б)

Рисунок 5.2

Например:

4. Для определения линейных токов при отключении фазы CA построим векторную диаграмму (рисунок 5.2а). В этом случае I_CA=0; I_A=I_AB-I_CA; I_B=I_BC-I_CA; I_C=I_CA-I_BC=- I_BC.

Таким образом, линейные токи I_A и I_C изменились, а I_B остался прежним.

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.04.2025225.68 Кб2методичка Средние века.DOC
#
02.06.2015294.97 Кб15методичка статистика 1-12экн-вв.pdf
#
03.11.2018223.74 Кб22Методичка ТОТВ.doc
#
02.06.20152.45 Mб330методичка ТП.docx
#
02.06.20151.44 Mб282Методичка экономика.pdf
#
01.07.20253.29 Mб2методичка электротех.doc
#
01.03.2025259.58 Кб1Методичка № 11. Риккетсии. Хламидии. Микоплазмы...doc
#
01.03.2025141.82 Кб1Методичка № 12 Спирохеты- возбудители сифилиса,...doc
#
24.04.2019115.2 Кб10Методичка № 14 Грипп.doc
#
24.04.2019152.58 Кб8Методичка № 16 ЧМ Клещ. энцефалит.doc
#
24.04.201989.09 Кб18Методичка № 2 Пневмок..doc