4. Определение надёжности попадания случайной величины в заданный интервал её изменения
4.1. Использование общей модели нормального распределения
Если по внешнему виду эмпирическая кривая распределения приближается к теоретической кривой нормального распределения, то приближённо можно считать, что
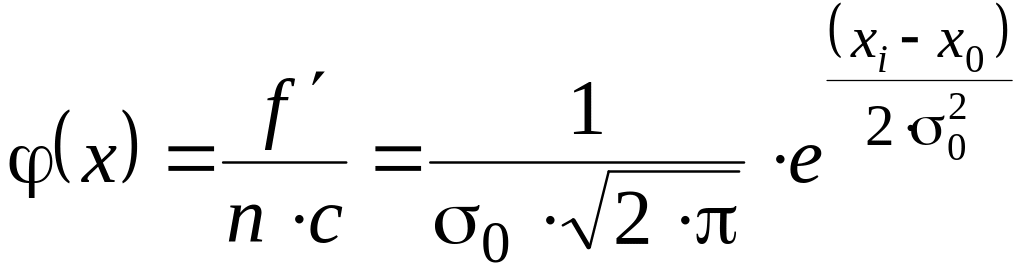, (5)
где φ(x) – общая математическая модель нормального распределения;
n – объём выборки;
f΄ – теоретическая частота;
x0 – среднее арифметическое значение х;
σ0 – среднее квадратичное отклонение параметра х;
с – цена интервала эмпирической совокупности.
Перепишем соотношение (1) в виде
Продолжение приложения 1
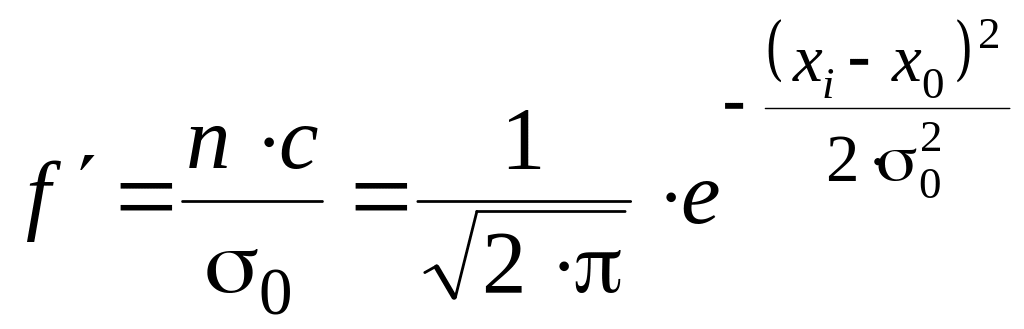, (6)
откуда
,
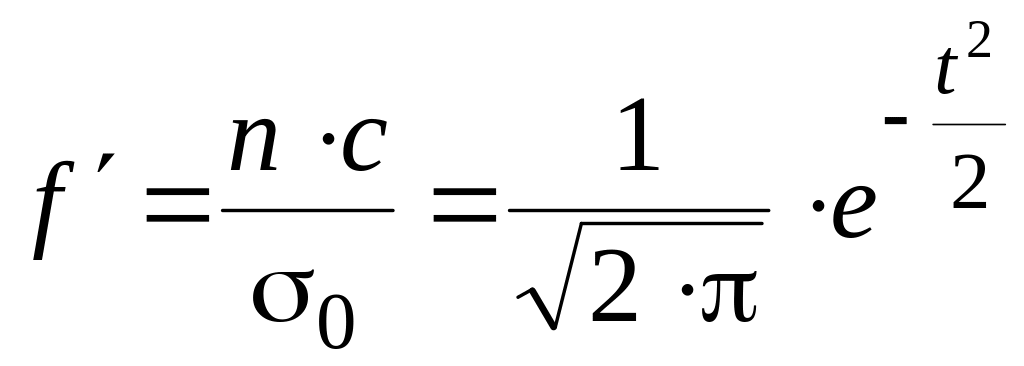или
,
где
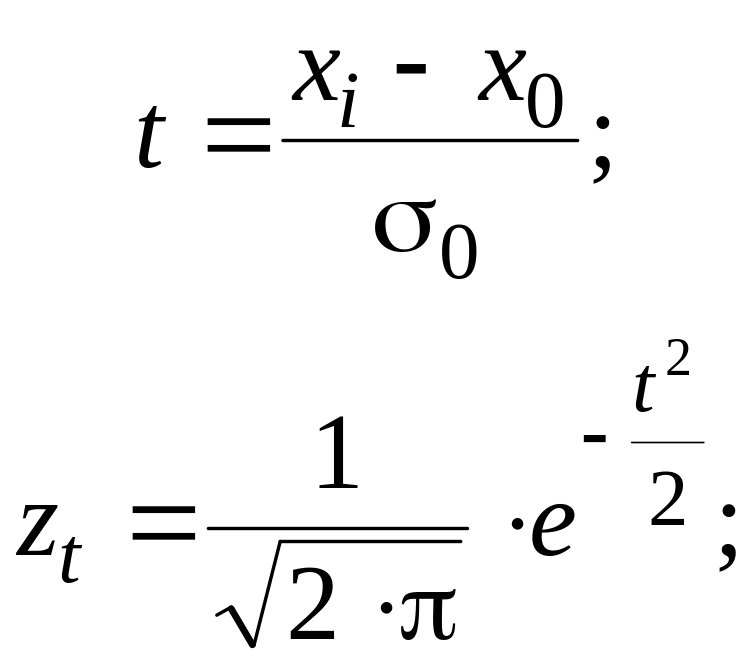
σ0=S.
Принцип расчёта теоретических частот нормального распределения при помощи функции zt, всегда положительной при ±t, приведён в таблице [1П.1, прил. 4, с. 203]. На основе расчётов составляют таблицу П1.18.
Таблица П1.18 – Вспомогательная таблица для вычисления теоретических частот нормального распределения при помощи функции zt
x |
xi
|
fi
|
|ti| |
zt |
|
f΄ с округлениями |
|
от |
до |
||||||
–0,14 |
–0,12 |
–0,13 |
3 |
2,07 |
0,0468 |
3,40 |
3 |
–0,12 |
–0,10 |
–0,11 |
16 |
1,35 |
0,1604 |
11,50 |
11 |
0 |
–0,08 |
–0,09 |
12 |
0,64 |
0,3251 |
23,50 |
23 |
–0,08 |
–0,06 |
–0,07 |
25 |
0,072 |
0,3980 |
28,55 |
29 |
–0,06 |
–0,04 |
–0,05 |
19 |
0,785 |
0,2940 |
21,45 |
22 |
–0,04 |
–0,02 |
–0,03 |
13 |
1,50 |
0,1295 |
9,20 |
9 |
–0,02 |
0 |
–0,01 |
2 |
2,20 |
0,355 |
2,60 |
3 |
|
|
|
100 |
|
|
|
100 |
Продолжение приложения 1
Пример расчёта
Для первой строки таблицы П1.18:
;
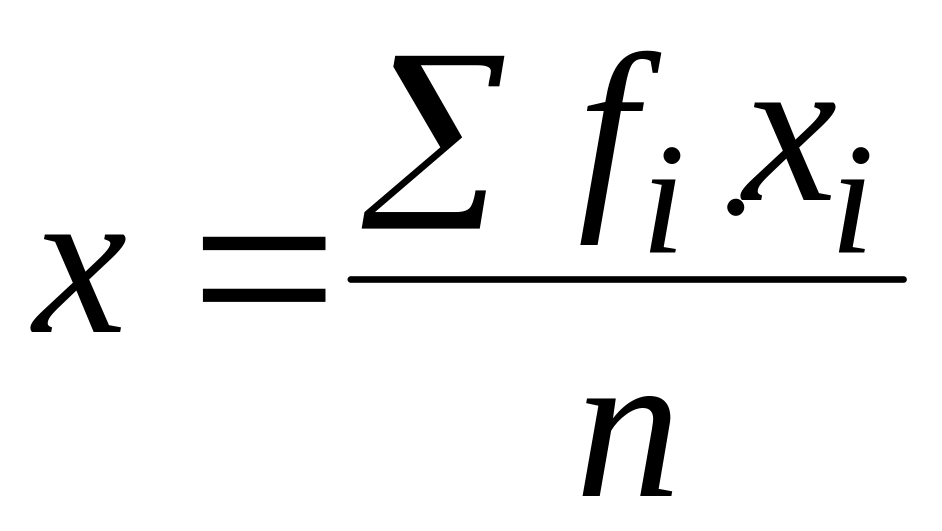x= –0,072;
;
S=0,028;
t=(–0,13+0,072)·0,028= –2,07.
Более детально расчёт может проводиться дополнением к таблице колонок xi·fi, xi–x, (xi–x)2 и fi·(xi–x)2. При этом xi принимают равным середине интервала.
Как и ранее, в ряду fi можно выделить значение теоретических частот для характерных точек, то есть для t=0, 1, 2, 3. Для этих значений t значения zt соответственно равны 0,4; 0,242; 0,054; 0.
Полученные значения теоретических частот наносят на график эмпирического распределения.
4.2. Использование интегральной модели нормального распределения
Графическое сопоставление эмпирического распределения с теоретически нормальным распределением можно производить также при помощи значений функции
Продолжение приложения 1
,
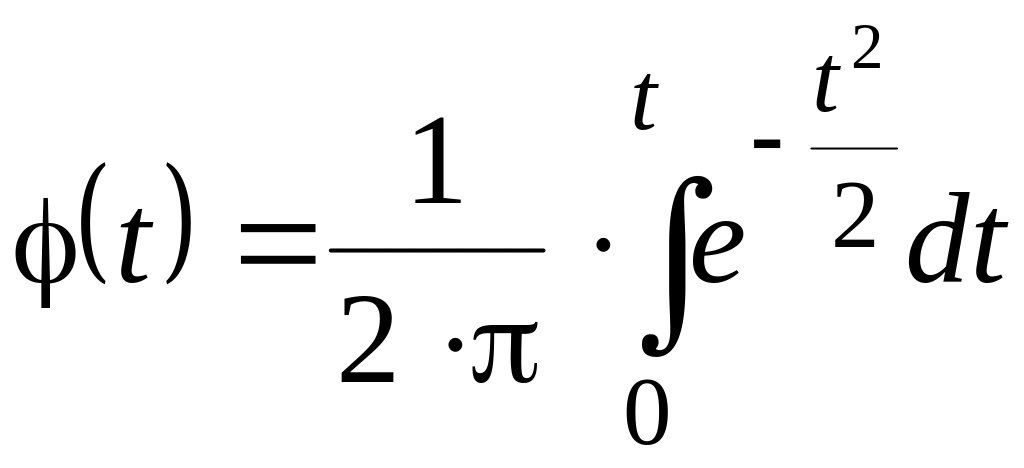которая
носит название нормированной интегральной
функции Лапласа, её значения для различных
приведены в таблицах математической
статистики [1П.1, с. 201]. Для этой цели, как
и ранее, прежде всего для каждого
интервала значений x
вычисляют t. При
этом для расчёта принимают верхнее
значение интервала, то есть
,
где xвз – верхнее значение х,
S – оценка значения σ.
Далее:
1) по t находят Φ(t) и функцию F(x)=0,5+Φ(t).
2) по величине F(x) определяют теоретическую частоту распределения f΄ по схеме:
а) для первого интервала
f΄1=F1(x),
б) для второго интервала
f΄2=[F2(x)–F1(x)]·n,
в) для любого последующего (i-го) интервала
f΄i=[Fi(x)–F(i–1)(x)]·n.
Пример.
Пусть S=0,028;
=
–0,072; n=100, интервал от
минус 0,14 до минус 0,12.
.
Продолжение приложения 1
Пример расчёта теоретических частот нормального распределения при помощи функции Ф(t) приведён в табл. П1.19.
Таблица П1.19 – Расчёт теоретических частот нормального распределения
x |
f |
t |
Ф(t) |
F(x)=0,5+Ф(t) |
f΄ |
f΄ с округлением |
|
от |
до |
||||||
–0,14 |
–0,12 |
3 |
–1,71 |
–0,457 |
0,043 |
4,30 |
4 |
–0,12 |
–0,10 |
16 |
–1,00 |
–0,341 |
0,153 |
11,6 |
12 |
–0,10 |
–0,08 |
22 |
–0,29 |
–0,114 |
0,386 |
22,7 |
23 |
–0,08 |
–0,06 |
25 |
0,43 |
0,166 |
0,666 |
28,0 |
28 |
–0,06 |
–0,04 |
19 |
1,14 |
0,373 |
0,873 |
20,7 |
21 |
–0,04 |
–0,02 |
13 |
1,86 |
0,468 |
0,968 |
9,50 |
9 |
–0,02 |
0,00 |
2 |
2,56 |
0,495 |
0,995 |
2,70 |
3 |
|
|
100 |
|
|
|
|
100 |
Полученные значения теоретических частот наносят на график эмпирического распределения, для чего строят на графиках кривых распределения заданные интервалы отклонений с отражением вероятности попадания в них случайной величины. При построениях используют общую и интегральную функции нормального распределения случайной дискретной величины (см. пособия 1П1 – 1П5).