РОЗДІЛ 7

ВИКОРИСТАННЯ МІЖГАЛУЗЕВОГО МЕТОДУ В

СТАТИСТИЦІ І ПРОГНОЗУВАННІ

1. Ціноутворення на основі міжгалузевого балансу

2. Особливості побудови міжгалузевих регіональних балансів

3. Міжрегіональна модель міжгалузевого балансу

4. Матрична модель виробничого планування на підприємстві

5. Застосування балансових моделей в маркетингу

1. Ціноутворення на основі міжгалузевого балансу

Для складання міжгалузевого балансу (таблиць "Витрати-випуск") виділяють три групи положень, які становлять базу для побудови статичної лінійної моделі таблиць "Витрати-випуск":

а) спосіб розгляду структури матеріального виробництва;

б) скінченність множини моделі видів продукції, включених у модель;

в) виділення екзогенних (значення задаються зовнішніми факторами) і ендогенних (значення задаються внутрішньою структурою) змінних у моделі;

г) характер залежності між витратами на виробництво й обсягом випуску продукції;

д) можливість передбачення на прогнозований період значень основних параметрів моделі – коефіцієнтів прямих витрат предметів праці a_ij;

ж) статичний характер моделі і відсутність у ній виробничих лагів;

е) відсутність чинників, що обмежують зростання виробництва продукції в перспективному періоді.

При достатньо великій кількості економіко-математичних моделей способи розподілу елементів структури виробництва в них зводяться до трьох основних типів. Відповідно визначають такі способи розподілу виробничої структури: продукт, технологічний варіант виробництва, організаційна форма діяльності.

Поняття "продукти" означає різні види вироблених матеріальних благ і послуг, що набувають форми предметів праці, засобів праці і предметів споживання. Ступінь деталізації, з якою розглядаються ці блага і послуги, залежить від конкретної постановки завдання і цілей.

Технологічний варіант виробництва обумовлюється в основному специфікою виробничого процесу з виготовлення продуктів. У результаті такого процесу може бути виготовлений один або декілька видів продукту. Технологічні варіанти виробництва одного і того ж продукту (або визначеного набору продуктів) можуть відрізнятись один від одного залежно від типу технологічного процесу, потужностей технологічних установок, способів їх розміщення тощо. Розбіжності в технологічних процесах спричинюють розбіжності обсягів та переліку випуску продуктів і витрат ресурсів при одній і тій же інтенсивності їх використання. За одиницю інтенсивності обирають одиницю часу ( година, місяць, рік), одиницю продукції або будь-який інший, комбінований вимірник (час виробництва одиниці продукції). Якщо в результаті виробничого процесу отримують декілька продуктів, то за основу береться час виробництва одного з них, а в інших враховується кількість одиниць (часток одиниці), що виготовляється за цей час.

В економіко-математичних моделях технологічні варіанти виробництва записують за допомогою векторів випуску продукції і витрат ресурсів A^s (s – індекс варіанта виробництва), компоненти якого A^s_is показують як виробництво продукції (із знаком "плюс"), так і витрати ресурсів (із знаком "мінус"). Як елементи виробництва розглядають елементи та форми економічної діяльності: виробниче підприємство, об’єднання підприємств, галузі, багатогалузеві комплекси, міністерства, а в деяких випадках і низові підрозділи підприємств (цехи і т. ін.). Кожна організаційна форма економічної діяльності характеризується або певним набором технологічних варіантів, або їх комбінацією.

При побудові різних економіко-математичних моделей ті самі об’єкти, залежно від поставлених завдань, можуть розглядатись і як технологічні варіанти виробництва, і як організаційні форми діяльності.

Використання моделі таблиці "Витрати-випуск" з метою прогнозування структури і динаміки розвитку економіки містить три логічно взаємозалежних етапи:

1) розрахунок і аналіз сформованих тенденцій зміни матеріально-речових міжгалузевих пропорцій за деякий ретроспективний період часу;

2) прогнозування на основі вказаного аналізу значень нормативних технологічних показників таблиць "Витрати-випуск" (коефіцієнти матеріаломісткості, капітало- і трудомісткості виробництва);

3) розробка і реалізація прогнозних балансів у системі поточних цін у розрахунку на використання отриманих результатів для складання балансів фінансових показників (баланс дохідних і видаткових статей державного бюджету, баланс грошових доходів і витрат населення, платіжний баланс).

Перший етап передбачає елементи формування цін. Складені в цінах відповідних років звітні таблиці "Витрати-випуск" ретроспективного періоду мають бути приведені в порівняний вигляд, тобто всі абсолютні показники, які враховуються у балансах, вимірюються в деякій системі незмінних цін базисного року. Позначивши в кожному році (τ) ретроспективного періоду [τ ₀, τ_n] (τ_{n –}останній рік часового періоду) фізичні обсяги валової продукції – x_i(τ), міжгалузеві потоки – , кінцеву продукцію Y_i(τ), які обчислюються в постійних цінах P_ij (i, j = 1, m – індекси видів продукції), то у грошовому виразі всі таблиці "Витрати-випуск" даного періоду записують:

.

(7.1)

У даній формулі ціна продукції кожного виду (P⁰_ij) диференційована відповідно до галузей-споживачів. Теоретично це пов’язано з урахуванням таких обставин:

1) у таблицях "Витрати-випуск" структура економіки розглядається в досить укрупненій номенклатурі, окремі позиції якої іноді включають багато сотень найменувань конкретних видів продукції, оцінюваних за відповідними індивідуальними цінами. У зв’язку з цим структура потоків, що визначаються рядком таблиці, буде неоднорідною щодо складу конкретних найменувань продукції, яка включається в дану позицію номенклатури таблиці. Таким чином, середні ціни на продукцію виду i, що витрачається різними споживачами, будуть відрізнятись;

2) ціни навіть на один і той самий однорідний вид продукції можуть бути різними для його конкретних споживачів. Наприклад, можуть бути встановлені більш низькі тарифи на споживання електроенергії в сільській місцевості порівняно з містами, виробничі підприємства можуть сплачувати споживання електроенергії за різними тарифами залежно від потужності устаткування й апаратури, що споживають енергію, тощо;

3) при розробці таблиць у цінах кінцевого споживання ціни на той самий вид продукції можуть відрізнятись через розходження в торговельно-транспортних націнках для окремих споживачів.

Однак при розв’язанні практичних задач неможливо врахувати подібні нюанси в ціноутворенні. Тому при грошовій оцінці міжгалузевих потоків x_ij(τ) використовується єдина ціна P⁰_ij, яка відрізняється від середньогалузевої, оскільки стосується лише тієї частини валової продукції виду i, що споживається у виробництві у вигляді поточних матеріальних витрат (оптові ціни виробників виступають як ціна P⁰_Пi. У цьому разі середньореалізаційна базисна ціна (0 – базисний рік) продукції виду і може бути визначена як:

,

(7.2)

де P⁰_ij – ціна продукції даного виду, що використовується для кінцевого споживання. Це споживчі або роздрібні ціни.

У визначеній у такий спосіб системі цін таблиці "Витрати-випуск" подаються у вигляді:

.

(7.3)

Основні показники безпосередньо порівняні в часі, оскільки в них відсутній чинник зміни цін.

На основі принципів, уже розглянутих при визначенні повних трудових витрат і повної капіталомісткості продукції, побудуємо систему цін, виходячи з такої схеми:

(7.4)

Коефіцієнти прямих матеріальних витрат (а_ij) і витрат праці (t_j) дані в натуральних одиницях, змінні Р₁, Р₂, Р₃, Р_n позначають ціни відповідних продуктів, а Р_t – грошовий еквівалент нової вартості, створеної за одиницю робочого часу. У балансі для кожного j-го продукту повинна бути рівність:

.

(7.5)

Вираз (7.5) утворить систему n лінійних рівнянь з n+1 невідомими величинами. Задавши значення однієї з них (це може бути ціна будь-якого продукту), величину Р_t можна знайти шляхом розв’язання системи (7.5) та визначити всі інші ціни. Повернемося до системи рівнянь, що визначає повні витрати праці, і помножимо її на величину Р_t . Одержимо:

.

(7.6)

Зіставивши останній вираз із системою (7.2), легко показати, що:

,

(7.7)

тобто збалансовані ціни продуктів у міжгалузевому балансі пропорційні величинам повної трудомісткості.

Наведемо ще одну формулу для розрахунку цін на вартісному рівні:

.

(7.8)

Формула (7.8) вимагає знання матриці коефіцієнтів повних матеріальних витрат і вектора прямих витрат праці.

Особливий характер носить величина P_t., з її допомогою, як видно з рівнянь (7.5), встановлюється в ціні Р_j вартість умовно-чистої продукції t_iP_t, пропорційна витратам живої праці. Величина Р_{j ,} очевидно, містить у собі в розрахунку на одиницю робочого часу вартість необхідного продукту, що цілком можна вважати відомою величиною, і вартість доданої вартості, що у загальному випадку нам невідома, але знаходиться в постійному співвідношенні до заробітної плати (у відповідності з вартісною формулою ціноутворення). Якщо коефіцієнти трудомісткості ti виражені в людино-годинах простої праці, v позначає нормативну ставку оплати однієї години простої праці, а α являє собою норму доданої вартості, то рівняння (7.5) може бути переписане в такий спосіб:

.

(7.9)

У цій системі, крім n цін, невідомою величиною є коефіцієнт . З погляду внутрішньої структури міжгалузевої моделі йі можливості розв’язання системи рівнянь величина останнього доданка у виразі (7.9) може мати будь-яке довільне значення. Нормувати коефіцієнт  на основі раціональних економічних передумов можна приєднанням додаткового (n+1)-го рівняння до системи (7.9).

Якщо дотепер у формулах цін брали участь лише структурні, а не об’ємні показники міжгалузевого балансу, то при побудові додаткового рівняння будемо виходити з того, що на перспективу визначені обсяги виробництва і кінцева продукція по всіх галузях (продуктах). Додаткове рівняння відображає вимогу відповідності доходів населення і суми цін товарів споживання домашніми господарствами:

.

(7.10)

Перший доданок рівняння (7.10) являє собою суму доходів населення, зайнятого у сфері виробництва фізичних обсягів продукції; величина D позначає задану суму доходів населення, зайнятого в невиробничій сфері; Р_j і y_j – відповідно ціни й обсяги кінцевих продуктів, призначених для споживання домашніми господарствами. Для практичних розрахунків рівняння (7.10) може бути скоректоване з урахуванням сплати податків, приросту заощаджень, оплати послуг нематеріального характеру і т.п., однак принципових змін у систему цін таке коректування не вносить.

Спільне вирішення рівнянь (7.9) і (7.10) дозволяє визначити ціни всіх продуктів і коефіцієнт , що являє собою норму чистого доходу стосовно оплати праці. Отримані ціни будуть пропорційні коефіцієнтам повних витрат праці, побудовані за єдиним принципом і забезпечать відповідність грошових доходів населення і суми цін товарів, що надходять в обіг.

Наведемо приклад розрахунку цін на вартісному рівні для умовної моделі, що складається з трьох напрямків діяльності. Де в якості напрямків діяльності виступають засоби праці, предмети праці і предмети споживання. Усередині кожного напрямку продукція вважається однорідною, що дозволяє обчислити коефіцієнти витрат у натуральному виразі. У таблиці 7.1 наведені коефіцієнти прямих матеріальних і трудових витрат (цифри умовні).

Таблиця 7.1

Коефіцієнти прямих витрат

Напрямки споживання	Засоби праці	Предмети праці	Предмети споживання
Напрямки виробництва
1. Засоби праці	0,2	0,1	0,1
2. Предмети праці	0,6	0,1	0,2
3. Предмети споживання	0	0	0
Праця (люд.-год.)	1,0	0,4	0,2

Прогнозований обсяг кінцевої продукції складає: y₁=10; y₂=0; y₃=20.

Базисна ставка оплати 1 людино-години простої праці v_н = 0,5. Насамперед розрахуємо коефіцієнти повної трудомісткості. Маємо таку систему рівнянь для розрахунку повних витрат праці:

,

(7.11)

Розв’язання цієї системи з трьох рівнянь із трьома невідомими дає такі значення для коефіцієнтів повної трудомісткості: Т₁ = 1,724; Т₂ = 0,636; Т₃ = 0,5.

Визначимо далі планові обсяги виробництва за напрямками діяльності на основі балансових рівнянь, що для даного прикладу мають вигляд:

,

(7.12)

Розв’язком рівнянь є такі значення обсягів виробництва: Х₁ = 17; Х₂ = 16; Х₃ = 20.

На підставі формул (7.9) і (7.10) складаємо систему рівнянь для розрахунку цін вартісного рівня (для простоти визначимо D = 0):

,

(7.13)

У результаті розв’язання рівнянь одержуємо: Р1= 2,366; Р2= 0,872; Р3 = 0,685;  = 1,74.

Зіставимо ці ціни з розрахованими раніше коефіцієнтами повних трудових витрат:

; ; .

(7.14)

Як бачимо, ціни за формулою вартості пропорційні повній трудомісткості. Коефіцієнтом пропорційності служить величина Р_t, яка дорівнює:

Рt = vн(1 + ) = 0,5 × 2,74 = 1,37.

(7.15)

За даними приклада складемо міжгалузевий баланс у цінах вартісного рівня, ґрунтуючись на розглянутих у розділі 3 математичних співвідношеннях міжгалузевої моделі.

Баланс приведений у таблиці 7.2.

Таблиця 7.2

Міжгалузевий баланс у цінах вартісного рівня

Споживання	Засоби праці	Предмети праці	Предмети споживання	Кінцева продукція	Валова продукція
Виробництво
Засоби праці	8,06	3,79	4,73	23,66	40,24
Предмети праці	8,89	1,57	3,49	-	13,95
Предмети споживання	0	0	0	13,70	13,70
Оплата праці	8,50	3,20	2,0		-
Чистий дохід	14,79	5,39	3,48		-
Валова продукція	40,24	13,95	13,70	-	67,89

Розраховані ціни забезпечують балансування показників у кожному рядку і колонці, а також рівність фонду оплати праці і вартості предметів споживання, сумарного чистого доходу і вартості кінцевої продукції засобів праці (зрозуміло, через спрощений характер прикладу й умовність вихідних даних структурні залежності тут далекі від реальних).

Міжгалузевий баланс дозволяє розрахувати систему цін за ціною виробника, з розподілом прибутку пропорційно капіталомісткості продукції. Якщо в розрахунку на одиницю j-ї продукції у виробництві задіяні засоби i-го виду, вартістю F_ij, то система рівнянь для розрахунку цін виробника має вигляд:

.

(7.16)

У формулі ціни j-го продукту перший доданок виражає вартість затрачених засобів виробництва, другий – витрати на оплату праці і третій – прибуток, норма якого стосовно вартості засобів визначається коефіцієнтом β.

Якщо вважати, що величини F_ij відомі, тобто засоби оцінені в іншій, чим шукана, системі цін, то серйозним методологічним недоліком застосування рівнянь (7.16) є поєднання двох систем ціноутворення. Воно має місце навіть у тому випадку, якщо раніше засоби були оцінені теж за цінами виробництва. Поряд зі старою оцінкою розв’язання системи (7.16) дає нову ціну всім елементам основних засобів, оскільки матриця коефіцієнтів а_ij включає коефіцієнти зносу (амортизації) основних засобів. Так утвориться подвійна ціна того самого продукту в системі рівнянь (7.16).

Для усунення цього недоліку варто виразити величини Fij через інші величини, що входять в систему (7.16). Стосовно основних засобів коефіцієнти а_ij показують, яка частка i-го засобу праці (у натурі) зношується в розрахунку на одиницю j-го виду продукції. Якщо, наприклад, машина виготовляє за рік 1000 одиниць продукції і служить 10 років, то відповідний коефіцієнт зносу дорівнюватиме 0,0001, тобто на одиницю продукції витрачається одна десятитисячна частина машини. Зайнята ж на одиницю річної продукції одна тисячна частина машини (при терміні служби 10 років). Якщо термін служби для i-го засобу праці позначити τ, то при коефіцієнті зносу а_ij капіталомісткість одиниці j-ї продукції по засобах j-го виду складе а_ijτ_i. Засоби i-го виду одержують у балансі оцінку P_i. Тоді можна записати:

Fij =aijτiPi.

(7.17)

Для оборотних засобів справедливим є те ж співвідношення, якщо τ_i показує, яку частку річної витрати i-го предмета праці представляє його нормативний запас.

На основі співвідношень (7.16) і (7.17) маємо таку систему рівнянь для розрахунку цін виробництва:

.

(7.18)

Термін служби основних засобів, а особливо норматив оборотних коштів пов’язані з характером тієї продукції, у виробництві якої вони беруть участь. Тому в загальному випадку доцільно розглядати показник τ диференційованим не тільки за видами засобів, але й за видами продукції, тобто вважати заданою матрицю коефіцієнтів τ_ij. З урахуванням сказаного система рівнянь цін виробництва набуває вигляду:

.

(7.19)

Невідомими величинами тут є ціни і коефіцієнт β, усього n + 1 перемінна при n рівняннях.

Для одержання цін виробництва на основі раціональних економічних передумов необхідно залучити об’ємні показники міжгалузевого балансу і до системи (7.18) чи (7.19) додати рівняння, що відображає умови відповідності грошових доходів і витрат населення.

Останній доданок у формулах (7.18) і (7.19) виражає додану вартість і безпосередньо визначає межі нагромаджень і капіталовкладень у народне господарство. Реалізована в ціні кожного продукту частина нагромаджень повинна за формулою ціни виробництва орієнтувати на забезпечення нормативної ефективності вкладень у створення потужностей з виробництва цього продукту. Тому в рівняннях цін виробництва норматив ефективності β має збільшуватися на питому суму вкладень у сучасних умовах виробництва.

Як відзначалося, динамічна модель міжгалузевого балансу передбачає розрахунок коефіцієнтів вкладень b_ij, що визначають витрати продукції i-го напрямку діяльності на розширення потужностей j-го виду діяльності в розрахунку на одиницю її річної продукції Лише в першому наближенні, за умови незмінності технології й організації виробництва, відсутності технічного прогресу, коефіцієнти вкладень b_ij можуть вважатися пропорційними коефіцієнтам поточних матеріальних витрат a_ij відповідно до описаної вище залежності:

bij = aijτij.

(7.20)

У дійсності ця пропорція порушується тим, що вкладення використовуються на сучасному рівні техніки і технології, тоді як у поточних витратах міжгалузева модель неминуче усереднює існуючі технологічні процеси як нові, так і відносно застарілі. Тому умовам відтворення більш відповідає така система рівнянь для цін виробництва:

.

(7.21)

Додаткове рівняння (7.16) залишається без зміни.

Зробимо розрахунок цін виробництва за даними розглянутої моделі на основі трьох напрямків діяльності. При цьому скористаємося рівняннями (7.15) і (7.16). Припустимо, що термін використання засобів праці складає 5 років, тобто в нашому прикладі τ_i=5. Для простоти в основні засоби будемо включати тільки засоби праці. Тоді система рівнянь для розрахунку цін виробництва набуває вигляду:

.

(7.22)

Розв’язок системи дає такі значення невідомих величин:

Р₁ = 1,814; Р₂ = 0,714; Р₃ = 0,685: β = 0,29.

Ціна предметів споживання через незмінність 4-го рівняння залишилася на вартісному рівні, інші ціни трохи зменшилися, і співвідношення між ними змінилися, так що ціни виробництва вже не пропорційні повним трудовим витратам. Міжгалузевий баланс у цінах виробництва подано у таблиці 7.3.

Як і у випадку вартостей, ціни виробництва забезпечують баланс за рядками і колонками, баланси за засобами споживання і нагромадження, однак структура валової продукції і кінцевого продукту за видами діяльності зазнала зміни, і підсумкові оцінки всієї продукції в цінах виробництва й у цінах вартісного рівня не збігаються. Конкретний аналіз змін, що відбулись, через умовності прикладу особливого інтересу не являє.

Міжгалузева модель дозволяє розрахувати ціни і при інших принципах розподілу прибутку, зокрема, при віднесенні частини прибутку в ціні пропорційно трудомісткості продукції, а іншої частини прибутку – пропорційно капіталомісткості.

Таблиця 7.3

Міжгалузевий баланс у цінах виробництва

Споживання	Засоби праці	Предмети праці	Предмети споживання	Кінцева продукція	Валова продукція
Виробництво
1. Засоби праці	6,17	2,90	3,63	18,4	30,84
2. Предмети праці	7,28	1,29	2,85	-	11,42
3. Предмети споживання	-	-	-	13,70	13,70
Оплата праці	8,50	3,20	2,0	-	-
Чистий доход	8,89	4,03	5,22	-	-
Валова продукція	30,84	11,42	13,70	-	55,96

Дотепер передбачалося, що для розрахунку цін є матриця коефіцієнтів витрат а_ij у натуральному виразі і відповідний міжпродуктовий баланс. Практично це припущення важко здійснити з ряду причин. Натуральні вимірники продукції вимагають її глибокої деталізації, що сильно ускладнює як збір необхідних даних, так і їх обробку навіть на найсучасніших обчислювальних машинах. Як би детально не був розроблений міжпродуктовий баланс, він не в змозі цілком охопити усі виробничі витрати, тому що деякі їхні види просто не піддаються натуральному виразу. Нарешті, у різного роду дослідженнях, у тому числі й з ціноутворення, важко обійтися без порівняно компактних балансів, що включають невелику кількість укрупнених напрямків діяльності, але це може бути здійсненим лише на основі застосування вартісних вимірників, а не натуральних. Таким чином, виникає питання про можливість визначення єдиної ціни за даними міжгалузевого балансу в вартісному виразі.

Сам по собі принцип використання вартісного балансу для розрахунку системи цін не може бути відкинутим без серйозного аналізу, однак необхідний певний критерій прийнятності такої системи цін.

Критерієм будемо вважати відповідність продукції в цінах, отриманих на базі вартісного балансу, її оцінці в "істинних" цінах, обумовлених за даними ідеального всеосяжного натурального балансу. Позначимо через а_ij коефіцієнти прямих матеріальних витрат у натуральному виразі, Х_i і Х_j – обсяги виробництва в натуральних одиницях за напрямками діяльності, р_i і р_j – вихідні ціни за одиницю продукції. Такі ціни загалом можна вважати довільними, що не відповідають безпосередньо якійсь формулі ціноутворення, ними можуть бути і чинні ціни. Матриця міжгалузевих потоків (I квадрант) балансу у вартісному виразі має вигляд:

.

(7.23)

Загальний вигляд елемента цієї матриці – а_ijХ_jр_i. Якщо усі компоненти визначені окремо, то ділення добутків міжгалузевих потоків на добутки вигляду Х_jр_i дозволить виділити матрицю коефіцієнтів витрат у натуральному виразі й визначити збалансовані ціни так, як описано вище.

Однак в агрегованому вартісному балансі виділити за кожним обсягом діяльності й обсяг виробництва в натурі, з одного боку, і ціну за одиницю, з іншого боку, неможливо, тому що продукція напрямку-агрегату не являється абсолютно однорідною. Тому в вартісному балансі ми можемо вважати відомими лише абсолютні величини міжгалузевих потоків (а_ijХ_jр_i) і обсяги виробництва за напрямками діяльності у ціннісному вираженні (Х_iр_i або Х_jр_j). Це не дозволяє отримати матрицю коефіцієнтів а_ij у чистому вигляді. Розподіл величин міжгалузевих потоків на обсяги продукції за напрямками споживання дає матрицю коефіцієнтів витрат у гривнях. Елементи матриці мають вигляд:

.

(7.24)

Застосовуючи коефіцієнти, показники витрат живої праці в розрахунку на 1 гривню продукції за напрямками діяльності і вважаючи незмінними інші величини в рівняннях цін, визначимо нові збалансовані ціни U_j (U_i) на основі системи рівнянь (7.6):

.

(7.25)

Відзначимо, що для розрахунку величин не обов’язково знати одиничні ціни р_j, досить розділити сукупні витрати живої праці за напрямками виробництва на обсяг її продукції в грошовому виразі. Помноживши (7.25) на р_j,одержимо:

.

(7.26)

Таким чином, "ціни" Uj, і Ui, що визначаються на основі рівнянь (7.25), являють собою по суті індекси, відношення "справедливої" ціни натурального міжгалузевого балансу до ціни вихідного (довільної, діючої і т.п.):

; .

(7.27)

Очевидно, що

(Xjpj)Uj =XjPj.

(7.28)

Інакше кажучи, множення обсягу продукції напрямку діяльності в вартісному виразі (у будь-яких цінах р_j) на індекс Uj дозволяє виразити продукцію даного напрямку діяльності в збалансованих цінах єдиного рівня. В отриманні індексів, "корегуючи" вихідні ціни, закладені в балансі, полягає глибокий зміст застосування розглянутих рівнянь цін до вартісного міжгалузевого балансу. Що ближче вихідні ціни відповідали цінам єдиного рівня, то менше індекси U_j будуть відрізнятися від одиниці.

Для напрямку діяльності, що поєднує кілька продуктів з різними цінами, величина U_j дає єдиний коефіцієнт перерахунку цін, застосування якого найбільше виправдане в тих напрямках діяльності, де ціни різних продуктів встановлені одноманітно, за загальним принципом, хоча і відмінному від принципу розрахунку самих коефіцієнтів U_j .

Скористаємося розглянутим вище прикладом для ілюстрації розрахунку цін на основі вартісного балансу. В таблиці 7.2 наведений міжгалузевий баланс у цінах вартісного рівня. Матриця коефіцієнтів для цього балансу має вигляд:

(7.29)

Користуючись цією матрицею й іншими даними прикладу, складемо систему рівнянь виду (7.25):

;	(7.30)
;	(7.31)
.	(7.32)

Розв’язок системи такий: U₁ = U₂ = U₃ =1.

Оскільки вихідними цінами балансу були ціни єдиного рівня, індекси, як і можна було очікувати, дорівнюють одиниці.

Дамо вихідним цінам довільні значення р1 = 2, р2 = 1, р3 = 0,5. За даними таблиці 7.1 і співвідношенням (7.24) одержимо у вихідних цінах таку матрицю коефіцієнтів витрат:

.

(7.33)

Коефіцієнти прямих витрат праці на 1 грн продукції складають 0,5; 0,4; 0,4. Валова продукція за напрямками діяльності у вихідних цінах дорівнює відповідно 34; 16 і 10. Тоді маємо таку систему рівнянь для розрахунку цін:

.

(7.34)

У результаті розв’язання системи одержуємо:

U₁ = 1,183; U₂ = 0,872; U₃ = 1,37; α = 1,74.

Перемноживши довільно узяті вихідні ціни на обчислені індекси, отримаємо ціни єдиного рівня, що збігаються з розрахованими раніше за даними натурального балансу:

Р₁ = 1,183×2 = 2,366; Р₂ = 0,872×1 = 0,872; Р₃ = 1,37×0,5 = 0,685;

Аналогічно за даними балансу в вартісному виразі можуть бути отримані індекси для оцінки продукції в збалансованих цінах виробництва за іншими формулами ціноутворення.

Економічні особливості й властивості цін міжгалузевого балансу випливають із загальних передумов, що лежать в основі міжгалузевого методу. При цьому поряд з позитивними якостями ціни несуть на собі й відображення певної умовності, обмеженості, що властиві міжгалузевим моделям.

Ціни на основі міжгалузевого балансу визначаються за єдиною методикою, за загальною формулою (чи то формула вартості, ціни виробництва і т.п.), з однаковим коефіцієнтом розподілу прибутку. Це сприяє ліквідації розриву в рівнях цін, подоланню різнобою в рентабельності продуктів і цілих напрямків виробництва. Відображаючи складні виробничі взаємозалежності, переплетення прямих і зворотних зв’язків в економічній системі, ціни міжгалузевого балансу відрізняються повною погодженістю і збалансованістю.

Єдині ціни показують, у що в середньому обходиться суспільству виробництво тієї чи іншої продукції, причому ціни вартісного рівня повністю пропорційні середнім повним витратам живої й уречевленої праці. Зіставлення цих цін з діючими дало б важливу інформацію, що дозволяє робити висновок про ступінь відповідності сформованої системи цін середнім витратам суспільної праці.

Ціни міжгалузевого балансу набагато точніші, ніж діючі ціни, дозволяють досліджувати величину і структуру суспільних виробничих витрат і основні народногосподарські пропорції: між виробництвом засобів виробництва і предметів споживання, фондами споживання і нагромадження в національному доході, між валовим і чистим продуктом, між найважливішими галузями виробництва і т.д. Для аналізу ефективності витрат і прогнозування розвитку виробництва великий інтерес являє зіставлення цін єдиного рівня за взаємозамінними видами сировини, палива, матеріалів, споживчих продуктів. Нарешті, ціни міжгалузевого балансу надають можливість уточнення оцінок ефективності зовнішньої торгівлі й удосконалювання різних міжнародних економічних зіставлень.

Поки не здійснюється оптимальне прогнозування в масштабах народного господарства й відсутня інформація для розрахунку оптимальних цін, визначення цін на основі міжгалузевого балансу, що практично може здійснюватись уже в даний час, сприяло б удосконалюванню ціноутворення.

Однак ціни міжгалузевого балансу дозволяють вирішити далеко не всі проблеми ціноутворення, особливо в системі оптимального функціонування економіки. Ціни, отримані на основі міжгалузевої моделі, є усередненими величинами, що не враховують розходжень в об’єктивних умовах виробництва тієї самої продукції. Значною мірою довільні передумови приймаються при встановленні нормативів прибутку в ціні. З усього цього випливає і невизначеність самої формули ціноутворення: баланс дозволяє розраховувати ціни на рівні вартості, ціни виробництва і т.п., причому не дає критерію для оцінки переваги будь-якої із застосовуваних формул. Застосування таких цін на практиці вимагало б їхнього коректування з урахуванням співвідношень виробництва і потреб (пропозиції та попиту), взаємозамінності продукції, її споживчого ефекту й інших факторів.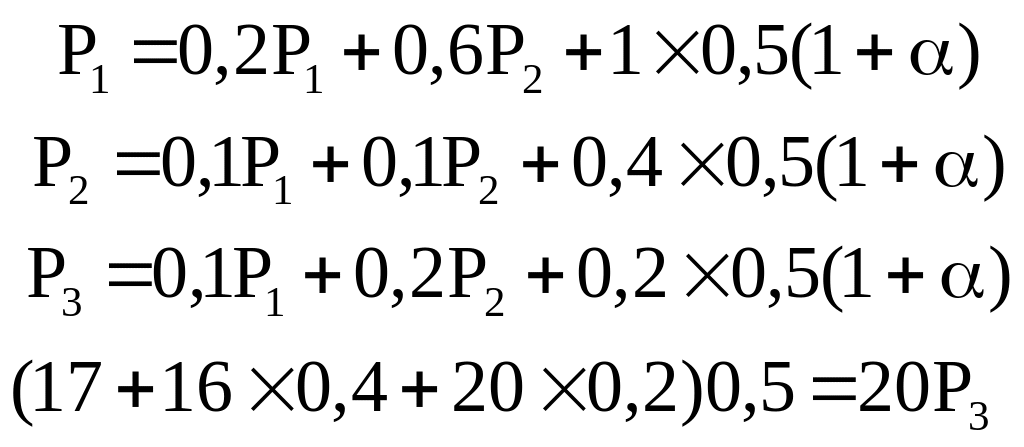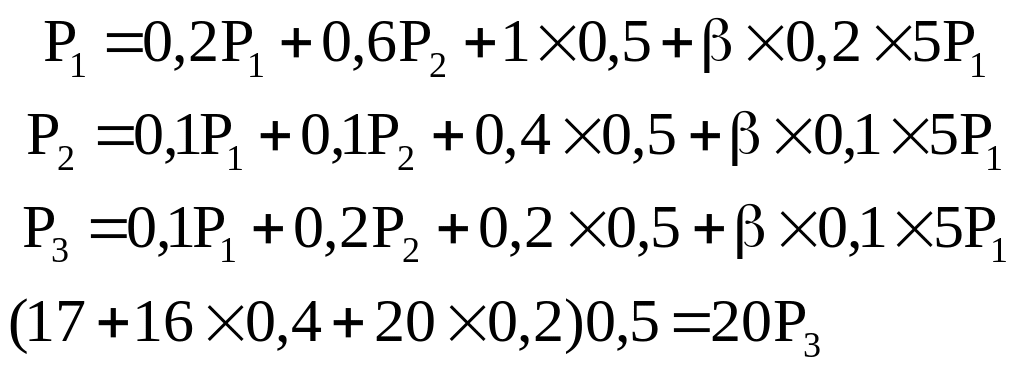
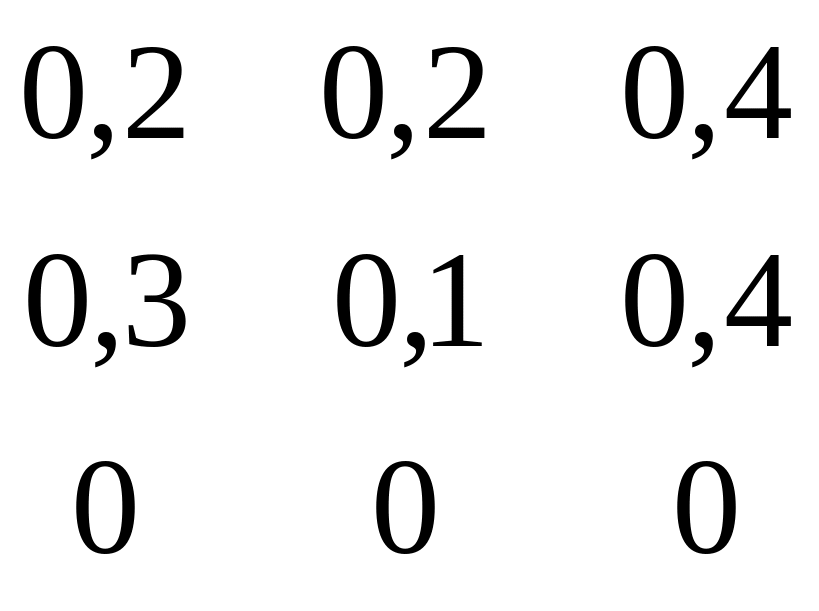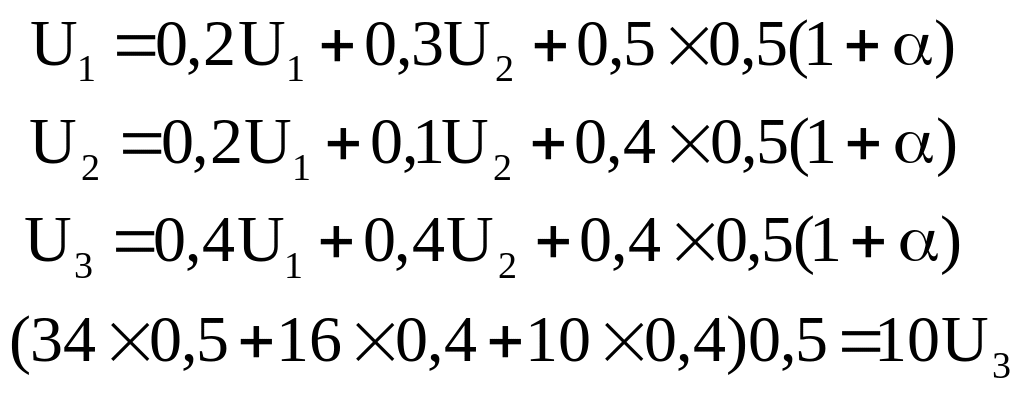