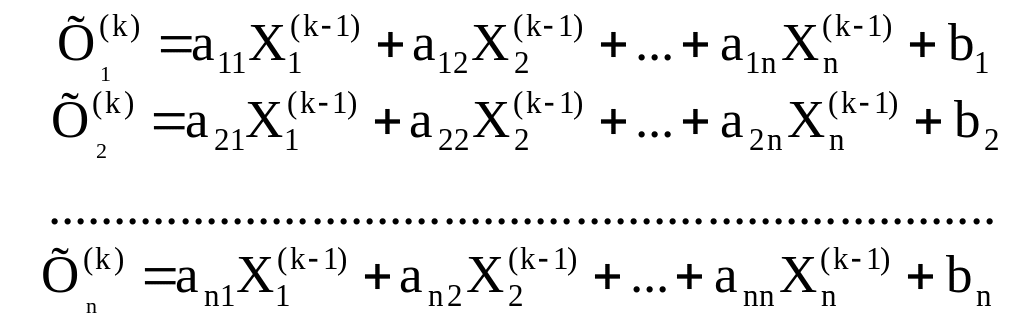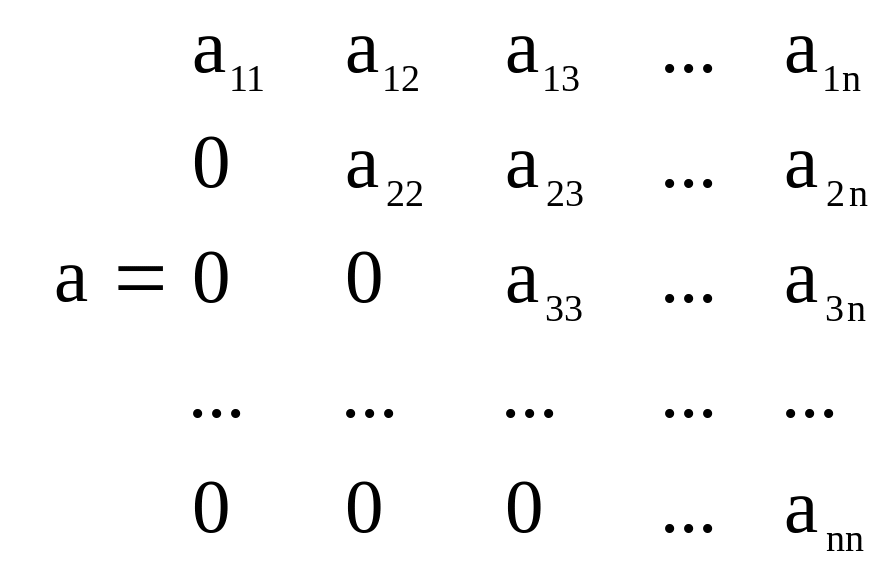3.3. Методи розв’язку матричних міжгалузевих моделей

Розрахунки в матричних моделях, що зводяться в головній частині до визначення обсягу валової продукції по заданій кінцевій продукції, можуть здійснюватися на базі одного з двох співвідношень. У першому випадку розрахунок ґрунтується на коефіцієнтах прямих витрат, у другому – на коефіцієнтах повних витрат. Для визначення валової продукції n напрямків діяльності при заданій кінцевій продукції необхідно вирішити систему n лінійних рівнянь з n невідомими. При значній кількості галузей це вимагає застосування спеціальних методів електронної обчислювальної техніки.

Розглянемо приклад розрахунку основних показників міжгалузевого балансу при умовному розподілі економіки усього на 3 сектори: промисловість, сільське господарство та інші. Припустимо, що на перспективу задана матриця коефіцієнтів прямих витрат а і вектор кінцевої продукції у (цифри умовні):

.

(3.35)

Необхідно провести розрахунок обсягів валової продукції на перспективу, величину міжгалузевих потоків, чисту продукцію напрямків діяльності і результати представити у формі міжгалузевого балансу. Для розрахунку валової продукції складемо систему рівнянь:

.

(3.36)

Перенесемо доданки, що містять невідомі величини в ліву частину рівнянь:

.

(3.37)

Для вирішення системи застосуємо метод послідовного виключення – метод Гаусса. При цьому методі на першому кроці розрахунків одне з рівнянь перетворюється так, щоб коефіцієнт при Х₁ дорівнював одиниці, а з інших рівнянь Х₁ виключається взагалі. На наступному кроці домагаються одиничного коефіцієнта при Х₂ у другому рівнянні і виключають Х₂ із усіх наступних рівнянь. Продовжуючи зазначену обчислювальну процедуру, одержують у кінцевому рахунку систему, у якій останнє рівняння містить лише одну невідому величину, а кожне попереднє – на одну більше (у загальному випадку). Потім шляхом зворотної підстановки, переходячи крок за кроком від останнього рівняння до першого, знаходять значення всіх невідомих величин.

У нашому прикладі зручніше трохи змінити послідовність рівнянь і третє переставити на перше місце. Перший крок полягатиме ось у чому: третє рівняння ділимо на – 0,1 і ставимо на перше місце; потім отримане рівняння множимо на 0,7 і окремо на – 0,15 і віднімаємо відповідно, але з 2-го і 3-го рівнянь. У результаті одержимо таку систему:

.

(3.38)

На наступному кроці ділимо 2-е рівняння на – 0,6 для того, щоб коефіцієнт при Х₂ став рівним одиниці. Отримане рівняння множимо на 0,955 і віднімаємо з 3-го рівняння. У підсумку маємо:

.

(3.39)

З останнього рівняння знаходимо: Х₃ = 26,38.

Підставляючи це значення в 2-і рівняння, одержимо: Х₂ = 41,02.

Нарешті, з 1-го рівняння маємо: Х₁ = 102,22.

Такі планові обсяги валової продукції трьох секторів, необхідні для забезпечення заданого рівня кінцевої продукції. Для складання балансу розраховуємо також міжгалузеві потоки засобів виробництва X_ij за формулою X_ij = а_ijХ_j. Одержуємо:

.

(3.40)

Результати обчислень (з точністю до 0,1) представимо у формі міжгалузевого балансу (табл. 3.3).

Таблиця 3.3

Баланс виробництва і розподілу продукції для трисекторної моделі

Напрямки споживання	Проми-словість	Сільське господарство	Інші	Кінцева продукція	Валова продукція
Напрямки виробництва
Промисловість	30,6	10,3	5,3	56	102,2
Сільське господарство	15,3	4,9	0,8	20	41,0
Інші	10,2	2,1	2,1	12	26,4
Чиста продукція	46,1	23,7	18,2	-	-
Валова продукція	102,2	41,0	26,4	-	169,6

Величина чистої продукції визначається тут як різниця між валовою продукцією напрямку діяльності і сумою міжгалузевих потоків у кожнім колонці. Так, для промисловості чиста продукція дорівнює 102,2 – (30,6 + 15,3 + 10,2) = 46,1; аналогічно розраховується чиста продукція для двох інших напрямків діяльності.

Таким чином, на основі завдань за рівнем кінцевого продукту і коефіцієнтів прямих витрат отримані цілком збалансовані перспективні показники загального виробництва продукції і її розподілів як між напрямками діяльності як засобів виробництва, так і для кінцевого використання.

Проілюструємо на тому ж прикладі інший шлях розрахунку, що базується на попередньому визначенні коефіцієнтів повних витрат. Для розрахунку повних витрат можна скористатися співвідношеннями типу (3.5), якщо як вектор кінцевої продукції сприймати одиничні вектори, що позначають випуск одиниці кінцевої продукції лише в якійсь одній з галузей. Дійсно, у цьому випадку система (3.5) визначає, скільки продукції всіх галузей необхідно зробити (і затратити), щоб випустити в сферу кінцевого споживання одну одиницю продукції даної галузі. Це цілком збігається з визначенням коефіцієнтів повних витрат.

У нашому прикладі потрібно знайти матрицю коефіцієнтів повних витрат для трьох секторів:

.

(3.41)

Це вимагає рішення трьох систем рівнянь, кожна з який включає три рівняння з трьома невідомими. Для розрахунку повних витрат на одиницю продукції промисловості необхідно розв’язати таку систему рівнянь:

(3.42)

Ця система збігається з раніше розв’язаною, з тією різницею, що як кінцева продукція тут фігурує лише одиниця в першій галузі. Розв’язавши систему, одержимо значення трьох коефіцієнтів повних витрат:

(3.43)

Наступна система рівнянь складається для розрахунку повних витрат на одиницю кінцевої продукції сільського господарства. На відміну від попередньої одиниця додається тут не до першого, а до другого рівняння:

(3.44)

У результаті розв’язання цієї системи маємо:

(3.45)

Третя система рівнянь визначає повні витрати на одиницю кінцевої продукції інших галузей:

(3.46)

Розв’язок системи дозволяє знайти матрицю повних витрат:

(3.47)

Запишемо повністю розраховану нами матрицю коефіцієнтів повних витрат для умовної трисекторної моделі:

.

(3.48)

Усі коефіцієнти повних витрат за величиною помітно перевищують відповідні коефіцієнти прямих витрат. Найбільше розходження спостерігається між повними і прямими витратами власної продукції кожної галузі: коефіцієнти повних витрат тут більше одиниці, тому що включають ту одиницю продукції, що входить у сферу кінцевого використання. Знаючи коефіцієнти повних витрат і зафіксувавши рівень кінцевої продукції, легко розрахувати весь обсяг виробництва за напрямками діяльності, скориставшись формулою (3.8). У нашому прикладі необхідний обсяг продукції промисловості складе:

Х1 = А11У1 + А12У2 + А13У3 = 1,58×56 + 0,469×20 +0,363×12 = 102,2.

(3.49)

Валова продукція сільського господарства:

Х2 = А21У1 + А22У2 + А23У3 = 0,276 ×56 + 1,22×20 + 0,103×12 = 41,0.

(3.50)

Обсяг продукції інших галузей:

Х3 =А31У1 + А32У2 + А3У3 = 0,187×56 + 0,117×20 + + 1,132×12 = 26,4.

(3.51)

Як бачимо, результати розрахунку валової продукції напрямків діяльності за формулами (3.5) і (3.8) цілком збігаються. Це служить, зокрема, перевіркою правильності зроблених обчислень. Разом з тим приклад підтверджує, що для однократних розрахунків зручніше скористатися системою (3.5), не вдаючись до визначення коефіцієнтів повних витрат, тому що це дозволяє скоротити обсяг обчислень.

У розглянутому прикладі для рішення систем лінійних рівнянь був застосований метод послідовного виключення Гаусса. Цей метод дуже ефективний як для ручних розрахунків, так і з використанням обчислювальної техніки. Його різновидом, також широко застосовуваним, є метод повного виключення Жордана-Гаусса. При цьому методі домагаються, щоб кожна невідома величина залишилася в кінцевому результаті лише в одному рівнянні й була вилучена не тільки з усіх подальших рівнянь (як у методі Гаусса), але також із усіх попередніх рівнянь. Тоді процес вилучення безпосередньо приводить до розв’язання системи, і відпадає необхідність у зворотній підстановці.

Поряд з точними методами практичне значення має наближений метод рішення систем лінійних рівнянь – метод ітерацій. Хід обчислень за цим методом розглянемо на тому ж прикладі. Початковий запис системи рівнянь повинен відповідати вигляду (3.5):

(3.52)

Процес розрахунків складається з ряду послідовних кроків (ітерацій). На першій ітерації перемінні прирівнюються до вільних членів рівнянь, тобто приймається: Х₁= 56; Х₂ = 20; Х₃ = 12. Ці значення змінних на другій ітерації підставляються в праву частину вихідних рівнянь і обчислюються нові значення невідомих величин:

(3.53)

Отримані значення змінних на третій ітерації знову підставляються у вихідну систему. Одержуємо:

(3.54)

Очевидно, що ітераційний процес може продовжуватися нескінченно, при цьому абсолютно точні значення невідомих величин ніколи не будуть отримані. Однак для практичних цілей завжди досить лише відносно точних розв’язків, обумовлених заздалегідь заданою мірою точності. Якщо, наприклад, розв’язок має бути отриманий з точністю до 0,01, то ітераційний процес може бути припинений, коли черговий розв’язок збігається з попереднім з точністю до трьох знаків після коми. У прикладі для цього буде потрібно не менше 15 ітерацій.

Метод ітерацій формально дуже простий, суворо циклічний, тому він легко програмується і реалізується для комп’ютерної техніки. Іншою його перевагою є властивість самовиправлення: окремі помилки, допущені в процесі розрахунків, не впливають на правильність остаточних результатів.

Наведемо формальний опис методу. Вихідна система рівнянь повинна бути представлена в такій формі:

(3.55)

У якості початкового (нульового) наближення вибирається сукупність вільних членів системи: Х₁⁽⁰⁾ = b₁; Х₂⁽⁰⁾ = b₂; …; Х_n⁽⁰⁾ = b_n. Кожна наступна ітерація базується на результатах попередньої. Для деякої k-ї ітерації маємо:

(3.56)

За формулами (3.56) можна одержати розв’язок з будь-якою точністю, якщо ітераційний процес сходиться. Є ще одна ознака збіжності ітераційного процесу: якщо максимальна сума абсолютних величин коефіцієнтів a_ij у правій частині рівнянь (3.55) менше одиниці, то процес ітерацій сходиться. Математично ця умова записується так:

.

(3.57)

Для перевірки збіжності можна скористатися і колонками матриці a_ij.

У нашому прикладі суми коефіцієнтів у рядках рівні:

(3.58)

Максимальна сума (0,75) менше одиниці, що є ознакою збіжності обчислювального процесу. Відзначимо, що розглянута ознака збіжності є достатньою, але не необхідною: ітераційний процес може сходитися й у системах рівнянь, де сума коефіцієнтів деяких рівнянь перевищує одиницю.

Видозміною методу простих ітерацій є ітераційний метод Зейделя. Розрахункові формули для k-ї ітерації за методом Зейделя мають вигляд:

(3.59)

На k-й ітерації значення X^к₁ визначається так само, як за методом простих ітерацій. Але при розрахунку X^к₂ величина Х₁ підставляється вже не в (k-1)-му, а в k-му наближенні (тільки що розрахованому). При обчисленні Х^к₃ обидві попередні невідомі (Х₁ і Х₂) підставляються в k-му наближенні. Нарешті, у формулу для Х^к_n підставляються в k-му наближенні всі невідомі, крім самої Хn.

У загальному випадку ітераційний процес за методом Зейделя сходиться швидше ніж за методом простих ітерацій.

Визначена складність і громіздкість обчислень при розрахунку обсягів продукції і коефіцієнтів повних витрат у матричних моделях обумовлена необхідністю обліку не тільки прямих, але й зворотних виробничих зв’язків. Якщо, скажемо, послідовність витрат типу вугілля – електроенергія – метали – машини відображає прямі зв’язки, то зворотніми будуть витрати електроенергії у вуглевидобутку, у виробництві електроенергії і т.п. Очевидно, що для всього суспільного виробництва глибоко характерні сполучення і переплетення прямих і зворотних зв’язків.

Однак у деяких прикладних моделях, що розробяються, наприклад, для обмеженої групи продуктів, для однієї чи декількох взаємозалежних напрямків виробництва, для окремих підприємств, витрати зворотного зв’язку можуть бути незначними чи бути відсутніми узагалі. В останньому випадку матриця коефіцієнтів витрат має трикутну форму, тобто всі її елементи, що знаходяться нижче (чи вище) від головної діагоналі, дорівнюють нулю.

(3.60)

Трикутна матриця коефіцієнтів відповідає такій виробничій системі, у якій будь-який продукт може витрачатися у своєму виробництві й у виробництві будь-якого наступного за ним продукту, але ніякий наступний продукт у виробництві попередніх продуктів участі не бере.

Розрахунки обсягів продукції і коефіцієнтів повних витрат на трикутних матрицях набагато спрощуються. Покажемо це на прикладі розрахунку повних витрат праці й проміжних продуктів, що переробляються послідовно, на одиницю кінцевої продукції – одягу.

Вихідні дані наведені в таблиці 3.4, де від’ємні числа позначають випуск продукції, а додатні коефіцієнти прямих витрат.

Згідно з умовними даними таблиці 3.4, на випуск одиниці льону-сирцю затрачається 0,5 людино-години праці; на одиницю очищеного льону витрачається 1,5 одиниці льону-сирцю і 0,2 людино-години праці і т.д.; на одиницю одягу прямо затрачається 0,1 одиниці льоноволокна, 0,2 одиниці ниток, 3,0 одиниці тканини і 2,4 людино-години праці.

Таблиця 3.4

Прямі затрати

Продукція	Льон-сирець	Очищений льон	Льоноволокно	Нитки	Тканина	Одяг
Льон-сирець	-1	1,5
Очищений льон		-1	1,3
Льоноволокно			-1	1,2		0,1
Нитки				-1	1,1	0,2
Тканина					-1	3,0
Одяг						-1
Праця	0,5	0,2	0,2	0,3	0,1	2,4

Розрахуємо повні витрати на одиницю одягу. Для цього складемо таблицю 3.5 і почнемо її заповнення з останніх колонок (крім рядка „праця”). Колонка "Одяг" переписується без змін. У колонці "Тканина" показано, що в розрахунку на одиницю одягу потрібно випустити 3 одиниці тканини, а для цього необхідно витратити 3,3 одиниці ниток.

Ці 3,3 одиниці плюс 0,2 одиниці льоноволокна, що прямо витрачаються на виробництво одягу, складають повну потребу в випуску льоноволокна 3,5 одиниці в стовпчику "Нитки". Вказаний випуск вимагає витрат ниток у кількості 1,2×3,5=4,2 одиниці, а з врахуванням витрат ниток безпосередньо на виробництво одягу загальний її випуск повинен складати 4,3 одиниці. Аналогічно визначимо витрати і випуск інших проміжних продуктів. Потім розраховується рядок "Праця" шляхом множення прямих витрат праці (табл. 3.5) на величину випуску кожного продукту. Сума трудових витрат (у колонці "Кінцевий випуск") відображає величину повних затрат праці на одиницю кінцевої продукції одягу.

Цифри зі знаком «мінус», що стоять на головній діагоналі матриці (табл. 3.5), є коефіцієнтами повних витрат засобів виробництва і праці на одиницю кінцевого випуску одягу, розраховані в рамках даного обмеженого комплексу продуктів. Ці коефіцієнти не мають загального значення, оскільки модель не відображає всіх народногосподарських виробничих зв’язків і навіть усіх прямих витрат на випуск одягу (витрат допоміжних матеріалів, обладнання та інше). Проте для окремих підприємств, виробничих об’єднань, напрямків діяльності відповідні розрахунки дозволяють правильно визначати потребу в проміжних продуктах для забезпечення заданого рівня кінцевої продукції. Як бачимо, у даному випадку розрахунок повних витрат не вимагає застосування спеціальних методів, а здійснюється елементарно.

Таблиця 3.5

Повні витрати

Продукція	Льон-сирець	Очищений льон	Льоно-волокно	Нитки	Тканина	Одяг	Кінцевий випуск
Льон-сирець	-8,4	8,4
Очищений льон		-5,6	5,6
Льоноволокно			-4,3	4,2		0,1
Нитки				-3,5	3,3	0,2
Тканина					-3,0	3,0
Одяг					-1	-1	1
Праця	4,2	1,12	0,86	1,05	0,3	2,4	-9,93

У багатьох матричних моделях шляхом відповідної зміни порядку чергування галузей (продуктів) можна привести матрицю коефіцієнтів витрат до приблизно трикутного вигляду, коли нижче від головної діагоналі залишаються лише нулі й малозначимі за величиною коефіцієнти. Для орієнтованих розрахунків таку матрицю можна вважати трикутною, що дозволить уникнути громіздких обчислень.
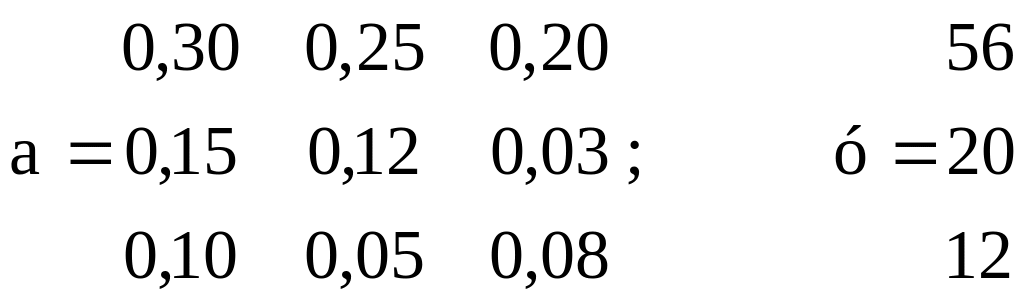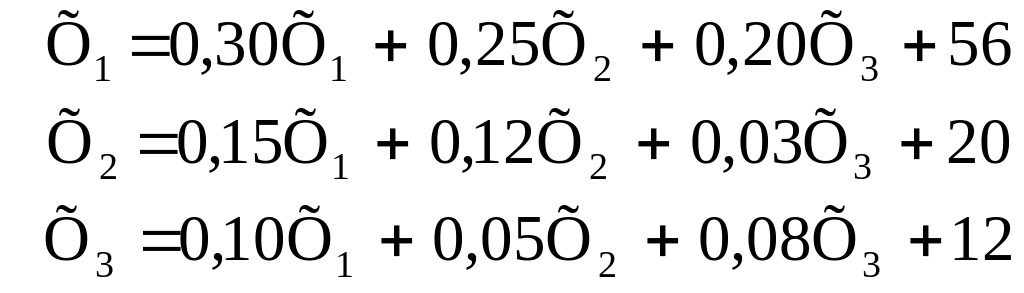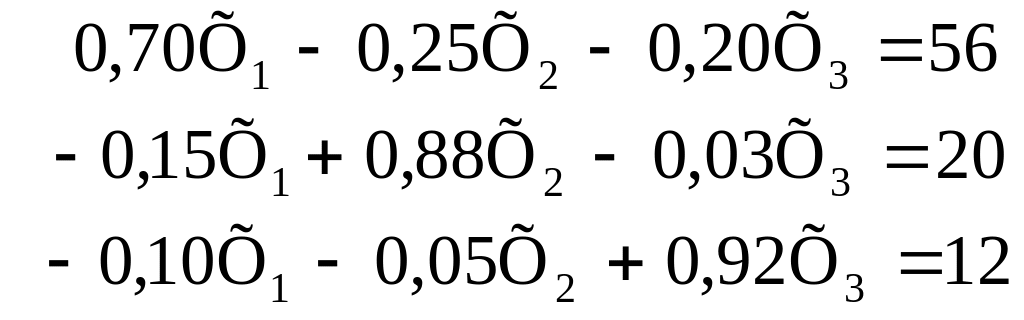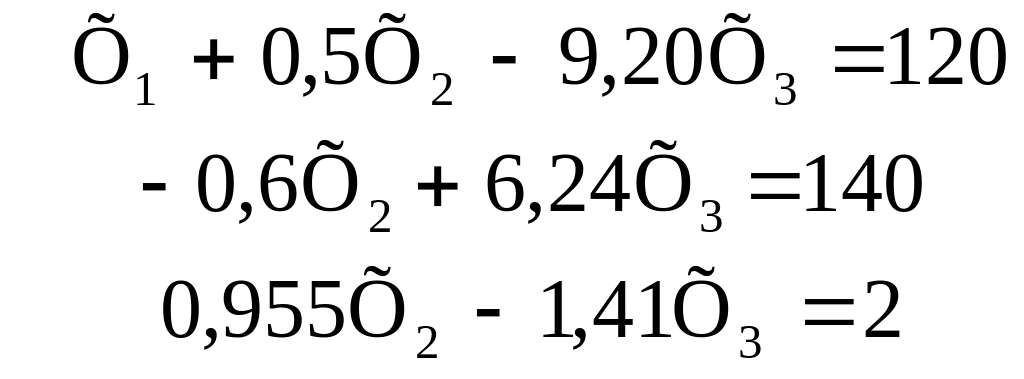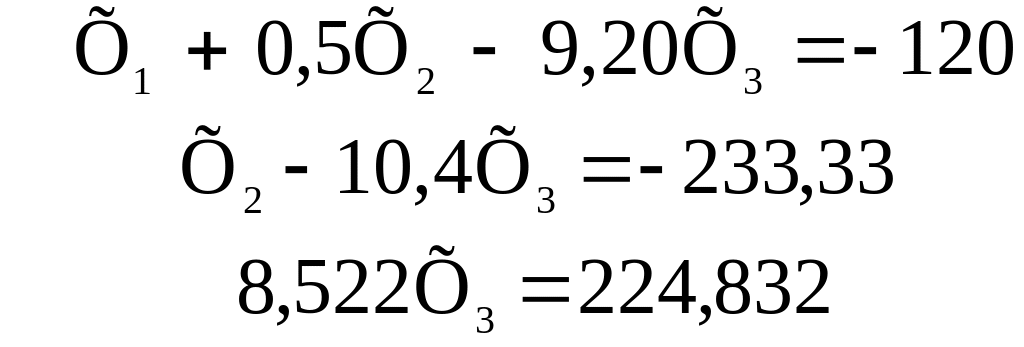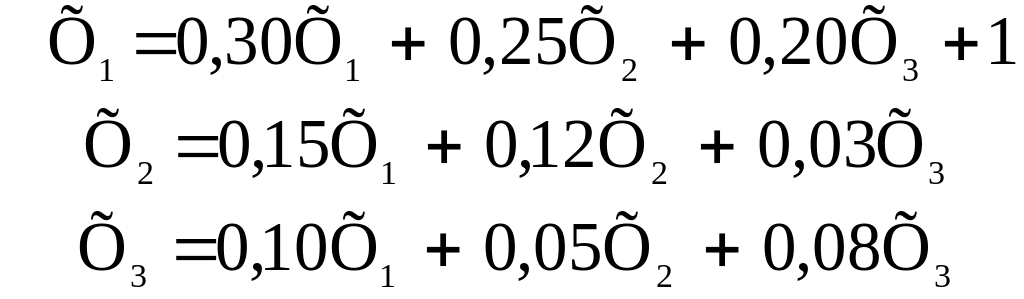
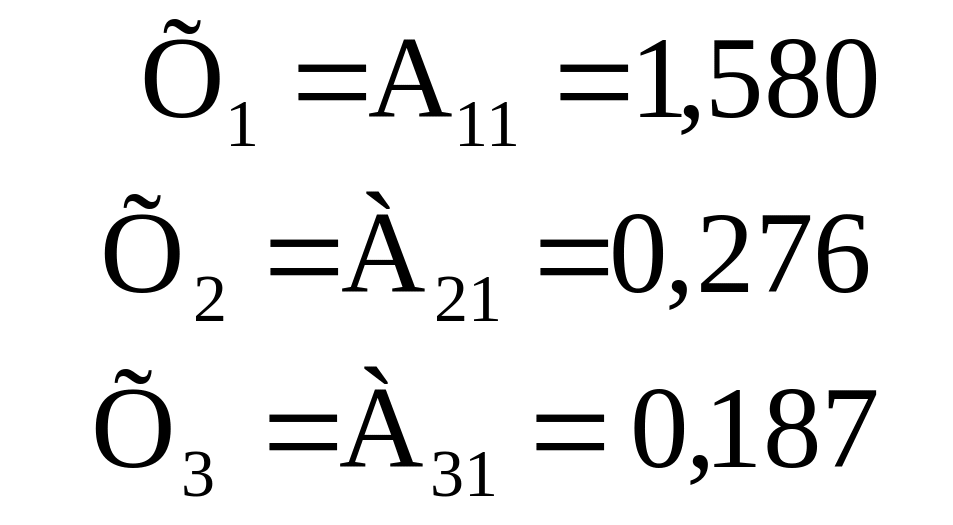
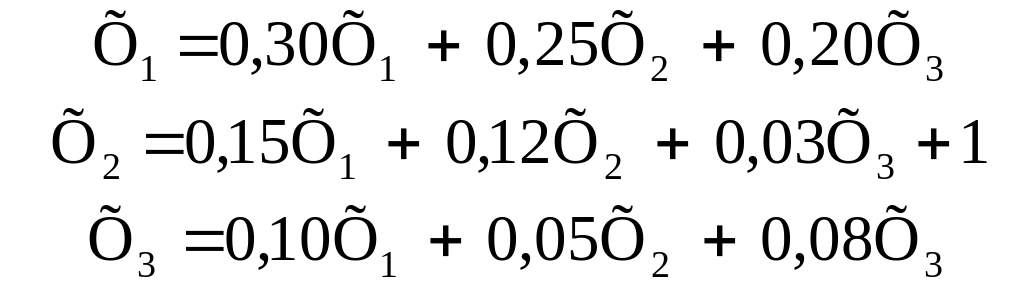
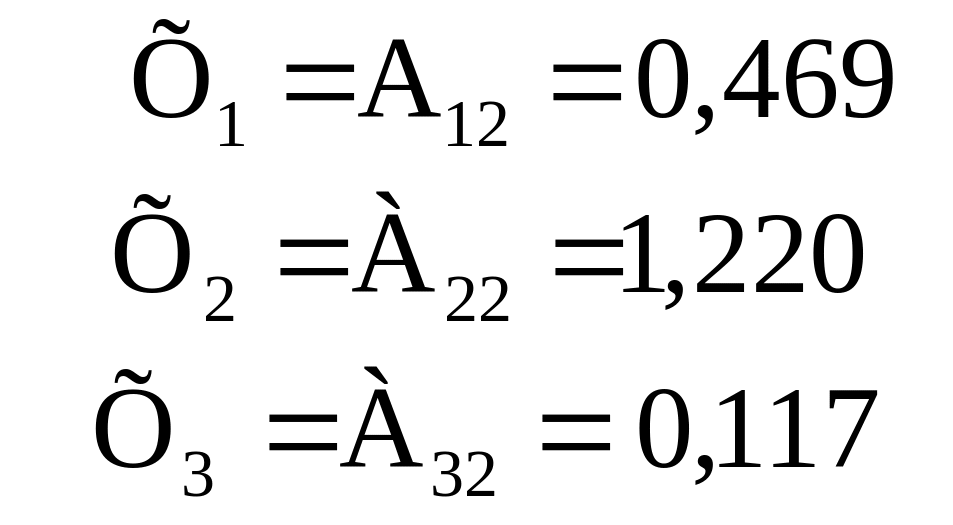
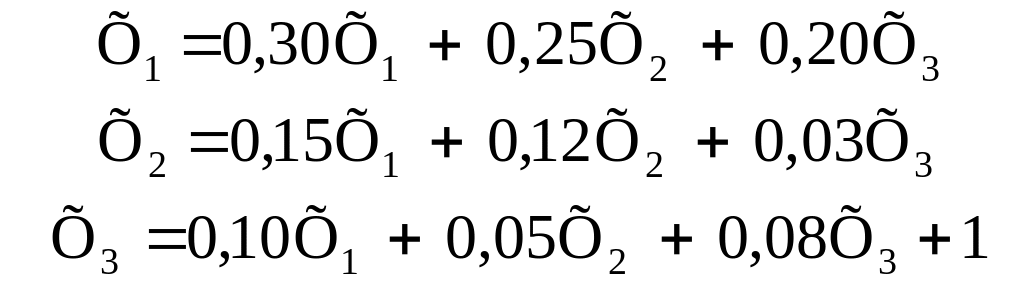
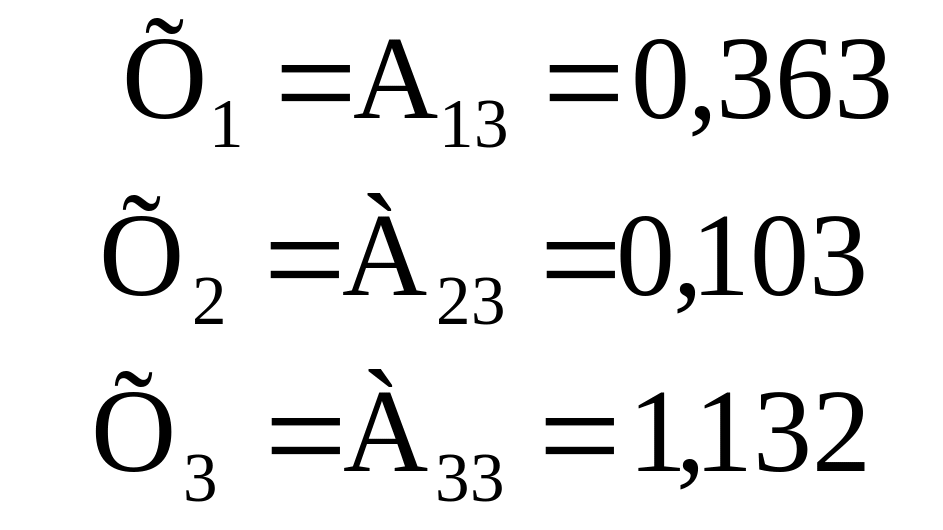
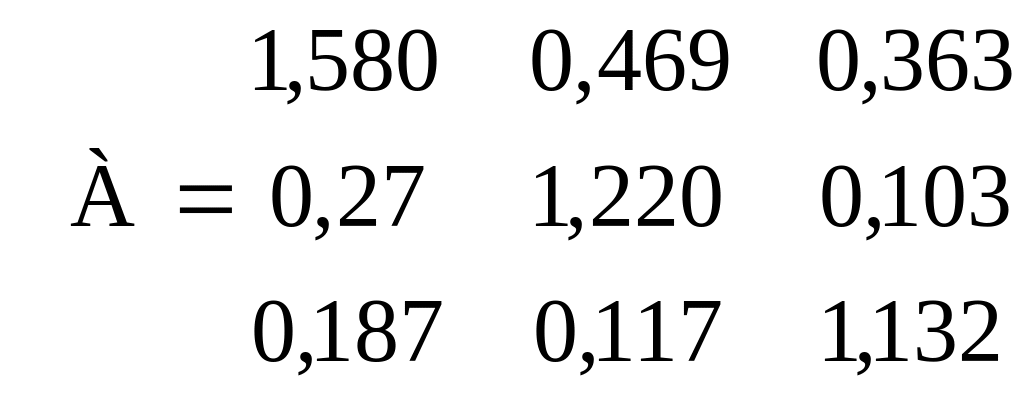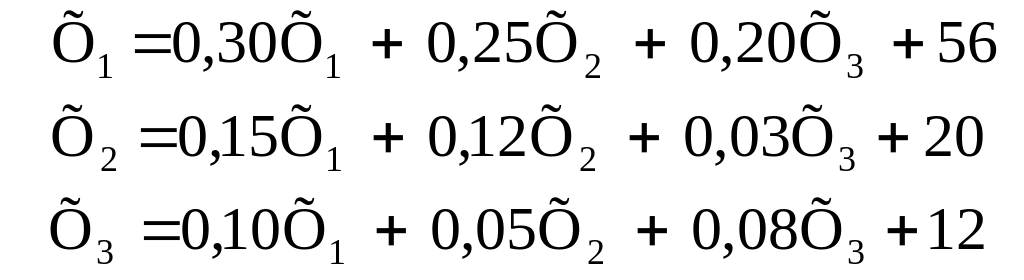
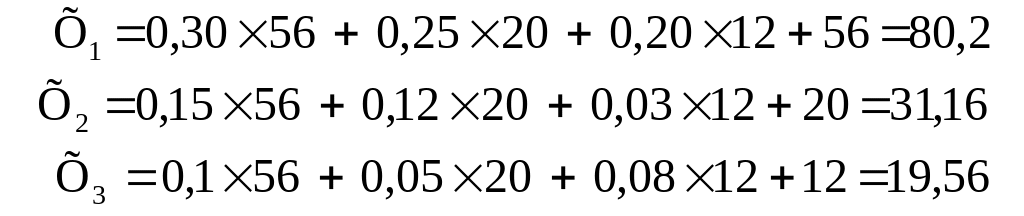
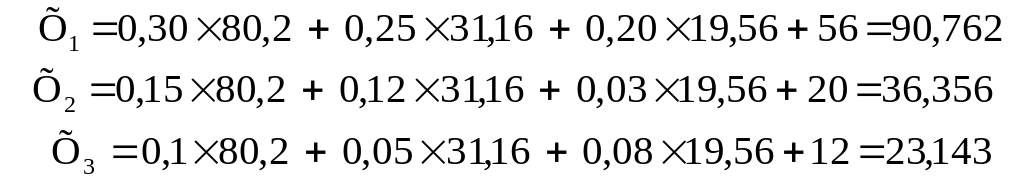
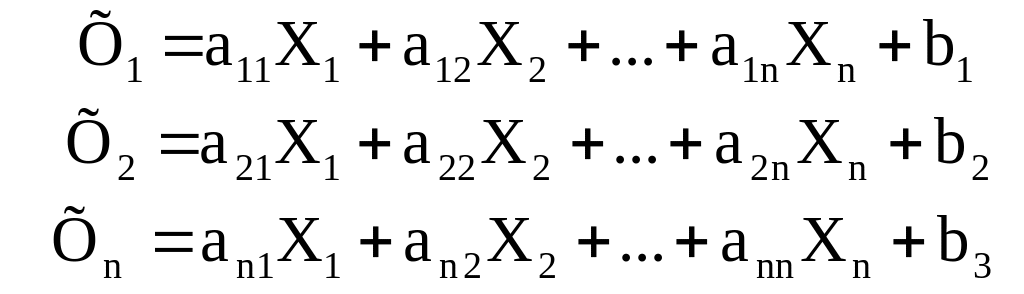
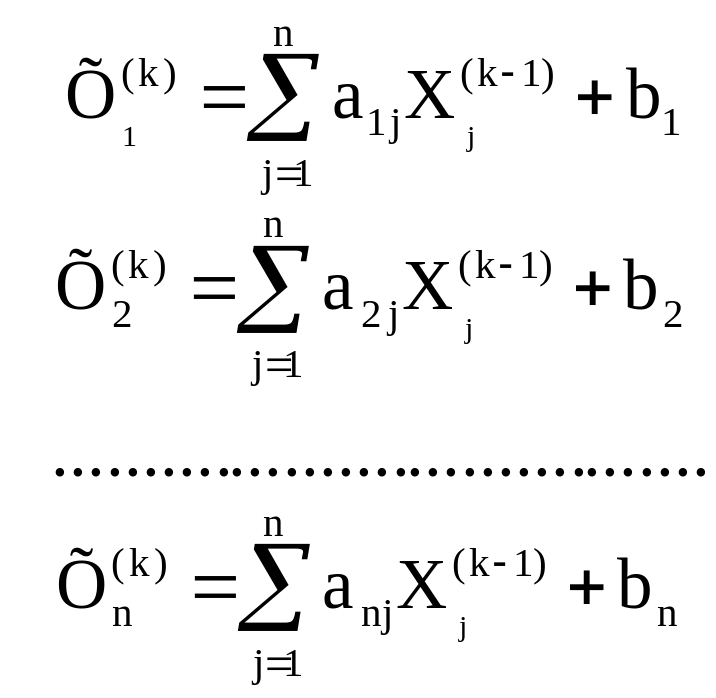
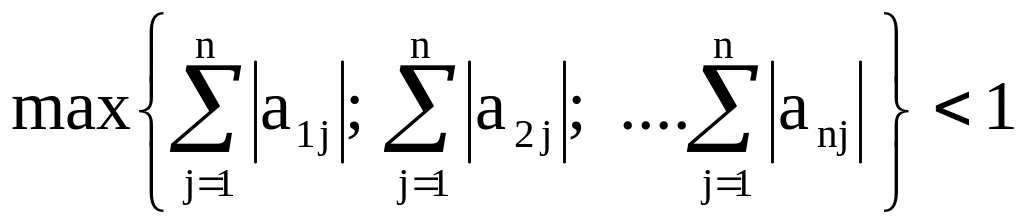