Задача 3. Анализ гетероскедастичности

Используя данные файла Рынокжилья.doc, постройте модели цен квартир разного типа, протестируйте качество моделей, наличие эффектов автокорреляции и гетероскедастичности. Дайте интерпретацию результатов.

Рынок жилья

Формирование цен на рынке первичного жилья

(на примере данных Санкт-Петербурга по состоянию на декабрь 2004 г.)

Для изучения формирования цен на рынке первичного жилья в Санкт-Петербурге создан файл Рынокжилья.xls (данные из него частично скопированы в лист «Задача 3» книги МУ.xlsx

Y - PriceUE	–	цена в у.е.
X1 - Rooms	–	количество комнат
X2 - Floor	–	этаж (фиктивная переменная): 0, если первый или последний; 1, иначе
X3 - Space	–	общая площадь (м2)
X4 - Type:	–	тип дома (фиктивная переменная):
X5 - Brick		кирпич
X6 - Brick-M		кирпич-монолит
X7 - Monolith		монолит
X8 - Panel		панель
X9 - Time	–	срок сдачи (мес.)
X10 -Transp	–	удаленность от метро (фиктивная переменная): 0, если не нужен транспорт; 1, иначе;
X11 - DistrictN	–	район (фиктивная переменная)
X12-Admiralteisky		Адмиралтейский
X13 -Vasileostrovsky		Василеостровский
X14-Viborgsky		Выборгский
X15-Kalininsky		Калининский
X16-Kirovsky		Кировский
X17-Krasno-gvardeisky		Красногвардейский
X18 Krasnoselsky		Красносельский
X19-Moskovsky		Московский
X20- Nevsky		Невский
X21-Petrogradsky		Петроградский
X22-Primorsky		Приморский
X23-Frunzensky		Фрунзенский
X24-Сentralny		Центральный

1. Проведите предварительный анализ переменных.

2. Сформулируйте гипотезы о влиянии независимых переменных на результирующую переменную (цена жилья).

3. Постройте модель вида линейную модель множественной корреляции.

4. Протестируйте модель (выполните проверку гипотез о значимости коэффициентов).

5. Обсудите значимость модели в целом (F-тест).

6. Обсудите качество модели (R²).

7. Дайте интерпретацию полученных результатов.

8. Проверьте прогнозные свойства полученных моделей для квартир с разным количеством комнат, обсудите полученные результаты. Что можно сделать для улучшения прогнозных свойств моделей?

9. Проверьте остатки на наличие автокорреляции (тест DW).

10. Проверьте исследование на наличие гетероскедастичности.

11. Обсудите возможные причины появления автокорреляции, гетероскедастичности и способы избавления от них.

Первый шаг – построение матрицы коэффициентов парной корреляции (лист «Задача 3»).

В полученной матрице множество ячеек с отметкой о делении на ноль. Это произошло вследствии того, что для примера была отобрана лишь незначительная часть исходных данных и некоторые переменные имеют постоянное значение. Удалим такие переменные из рассмотрения: Х7, Х8, Х14-Х24. Перенесем исходные данные на лист «Задача 3_1» и там произведем удаление.

Снова построим матрицу коэффициентов парной корреляции.

Проанализируем ее на наличие мультиколлинеарности (наличие тесных связей между факторами). Обычно считают, что мультиколлинеарность имеет место, если коэффициент парной корреляции между факторами превышает значений r=0.7. Это наблюдается между факторами Х3 и Х1, Х5 и Х4, Х6 и Х4, Х6 и Х5, Х12 и Х11, Х13 и Х11, Х13 и Х12.

Т.к. фактор Х3 сильнее связан с признаком (r(X3,Y)=0.772, r(X1,Y)=0.660), то оставляем в модели его.

Из тройки (Х4, Х5, Х6) оставляем Х6 (модули коэффицентов парной корреляции с признаком одинаковы, поэтому разницы нет).

Из тройки (Х11, Х12, Х13) оставляем Х13.

Снова переносим таблицу на новый лист «Задача 3_2», удаляем столбец Х1 и проводим заново расчеты коэффициентов парной корреляции, а затем строим линейное уравнение регрессии.

Уравнение регрессии адекватно, т.к. значимость F-критерия Фишера чрезвычайно мала, нормированный квадрат множественного коэффициента корреляции равен 0.72, т.е. 72% изменения признака объясняются изменением факторов.

Анализ коэффициентов уравнения регрессии показывает, что p-значение (уровень значимости) коэффициентов при Х6 и Х10 превышает значение 0.05. Следовательно, их необходимо удалить из модели.

Перенесем таблицу на лист «Задача 3_3», удалим эти переменные и упорядочим строки по возрастанию наиболее значимого фактора Х3 при помощи пункта «Сортировка и фильтр» ленты «Данные». При этом во всплывающем предупреждении указать необходимость автоматического расширения диапазона (рис. 12).

Рис. 12. Сортировка данных

После осуществления этих действий снова проводим регрессионный анализ, причем в панели «Регрессия» отмечаем пункт «Остатки». Остатки определяются как разность между наблюдаемыми значениями признака и вычисленными по уравнению регрессии:

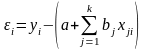
Здесь i – номер наблюдения, j – номер фактора, k – количество факторов.

Как можно заметить (см. табл. 9), нормированный коэффициент корреляции практически не изменился, значимость критерия Фишера улучшилось. Уравнение регрессии имеет вид:

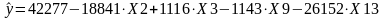
Таблица 9.

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,861801
R-квадрат	0,7427
Нормированный R-квадрат	0,719829
Стандартная ошибка	16806,47
Наблюдения	50
Дисперсионный анализ
	df	SS		MS		F		Значимость F
Регрессия	4	3,67E+10		9,17E+09		32,47336		9,62E-13
Остаток	45	1,27E+10		2,82E+08
Итого	49	4,94E+10
	Коэффици-енты	Стандартная ошибка		t-статистика		P-Значение		Нижние 95%		Верхние 95%
Y-пересечение	47277,07	10480,24		4,511068		4,59E-05		26168,78		68385,35
X2	-18841,6	5206,168		-3,61909		0,000746		-29327,3		-8355,83
X3	1116,169	101,2044		11,02886		2,22E-14		912,3325		1320,005
X9	-1142,9	582,5684		-1,96184		0,055985		-2316,26		30,44873
X13	-26152,2	8559,657		-3,05529		0,003772		-43392,3		-8912,19

Проанализируем теперь наличие автокорреляции и гетероскедастичности.

Для этого скопируем остатки, перенесем их на лист «Задача 3_4».

Для проверки автокорреляции скопируем столбец остатков (столбец A) и вставим его в столбец В на одну строку ниже.

Вызовем функцию «Корреляция» мастера анализа данных и найдем коэффициент корреляции между данными столбца А (А3:А51) и столбца В (В3:В51) (табл. 10).

Таблица 10.

Корреляция

	Столбец 1	Столбец 2
Столбец 1	1
Столбец 2	0,37585	1

Коэффициент корреляции равен r=0.376.

Для оценки значимости составим критерий Стьюдента:

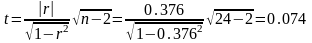
Для доверительного уровня 5% и числа степеней свободы 22 критическое значение критерия найдем при помощи функции «СТЬЮДЕНТ.ОБР.2Х(α; k)».

Т.к. 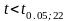, то гипотезу о наличии автокорреляции отвергаем.

Проверим теперь гипотезу о гомоскедастичности. Для этого отдельно скопируем верхнюю половину столбца остатков и поместим его в столбец D, а нижнюю – в столбец Е.

Через мастера анализа данных вызовем функцию «Двухвыборочный F-тест для дисперсии» (рис. 13-14).

Рис. 13. Выбор функции

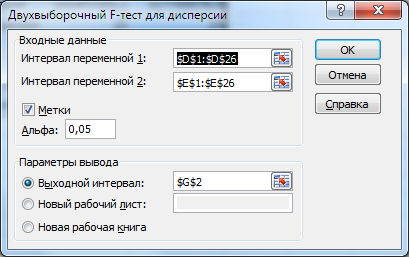
Рис. 14. Пример заполнения панели F-теста

Результат расчетов приведен в табл. 11.

Расчетное значение критерия Фишера равно 0.237, в то время как критическое значение – 0.504.

Т.к. F_расч<F_крит, то гипотезу о гомоскедастичности принимаем.

Таким образом, полученным уравнением регрессии можно пользоваться (на уровне значимости 0.05).

Таблица 11.

Двухвыборочный F-тест для дисперсии
	Остатки 1	Остатки 2
Среднее	-405,3321882	405,3321882
Дисперсия	101497205,1	427768078,6
Наблюдения	25	25
df	24	24
F	0,237271573
P(F<=f) одностороннее	0,000398816
F критическое одностороннее	0,504093347