Тema 2. Побудова загальної лінійної економетричної моделі

2.1. Основні положення

Для того щоб кількісно описати зв’язок між кількома або багатьма змінними, одна з яких є залежною, інші — незалежними змінними, необхідно розглянути лінійну економетричну модель, яка базується на регресійному аналізі.

У загальному вигляді цю модель можна записати так:

де — залежна змінна; — незалежні змінні.

Увага! число незалежних змінних.

Залежна змінна називається також пояснюваною, ендогенною змінною, незалежні змінні — пояснюючими, екзогенними змінними.

Аналітична форма загальної лінійної економетричної моделі:

,

де — параметри моделі.

Нехай — вектор оцінок параметрів моделі.

Оператор оцінювання параметрів моделі на основі 1МНК:

Тут застосовані такі позначення:

матриця, що має рядків ( число спостережень) та стовпчик. Перший стовпчик цієї матриці складається з одиниць, решта стовпчиків – емпіричні значення незалежних змінних.

Тобто:

.

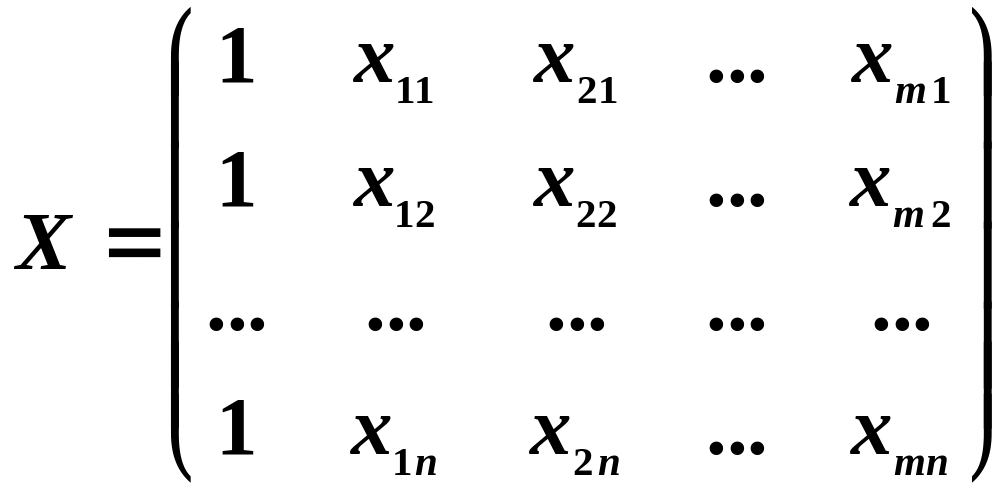транспонована матриця.

Вектор-стовпчик:

- елементами цього вектора є емпіричні значення незалежної змінної.

2.2. Загальна економетрична модель: побудова й аналіз

Приклад 2. Побудувати економетричну модель, яка характеризує залежність між витратами на харчування, загальними затратами та складом сім’ї на основі даних, наведених у табл. 2.1. Проаналізувати зв’язок, визначений на основі побудованої моделі.

Таблиця 2.1

Вихідні дані

№ п / п	Витрати на харчування	Загальні затрати	Склад сім’ї
1	20	45	1,5
2	32	75	1,6
3	48	125	1,9
4	65	223	1,8
5	45	92	3,4
6	64	146	3,6
7	79	227	3,5
8	104	358	5,5
9	68	135	5,4
10	93	218	5,4
11	117	331	5,3
12	145	490	8,5
13	91	175	8,3
14	131	205	8,1
15	167	468	7,3
16	195	749	8,4

Розв’язання:

1. Ідентифікуємо змінні моделі:

— витрати на харчування (залежна змінна);

— загальні витрати (незалежна змінна);

— розмір сім’ї (незалежна змінна).

Загальний вигляд моделі:

.

2. Специфікуємо модель, тобто в даному випадку визначимо її аналітичну форму:

.

3. Оцінимо параметри моделі на основі методу 1МНК, попередньо висунувши гіпотезу, що всі чотири передумови для його застосування дотримані.

Оператор оцінювання на основі 1МНК:

;

;

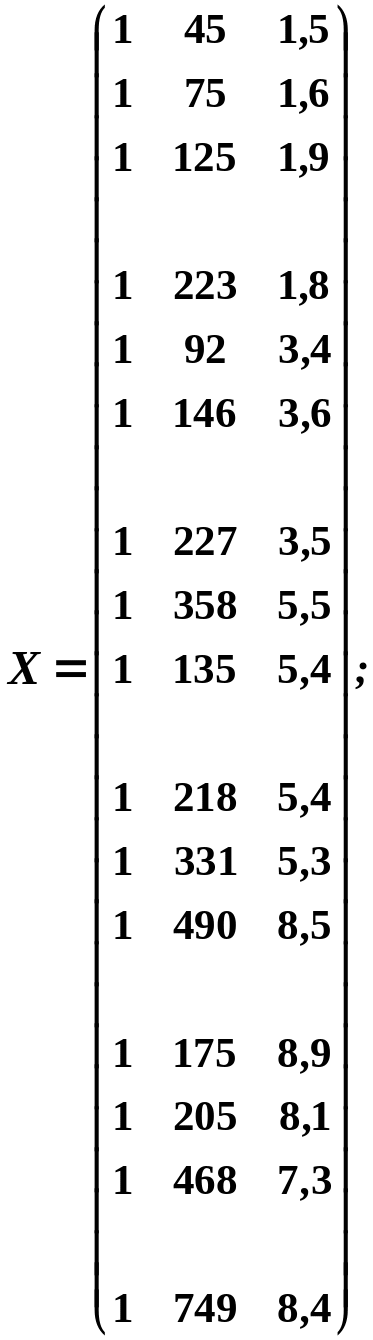
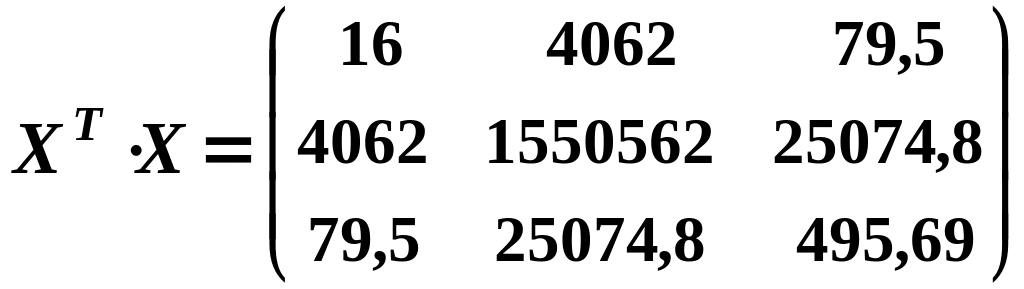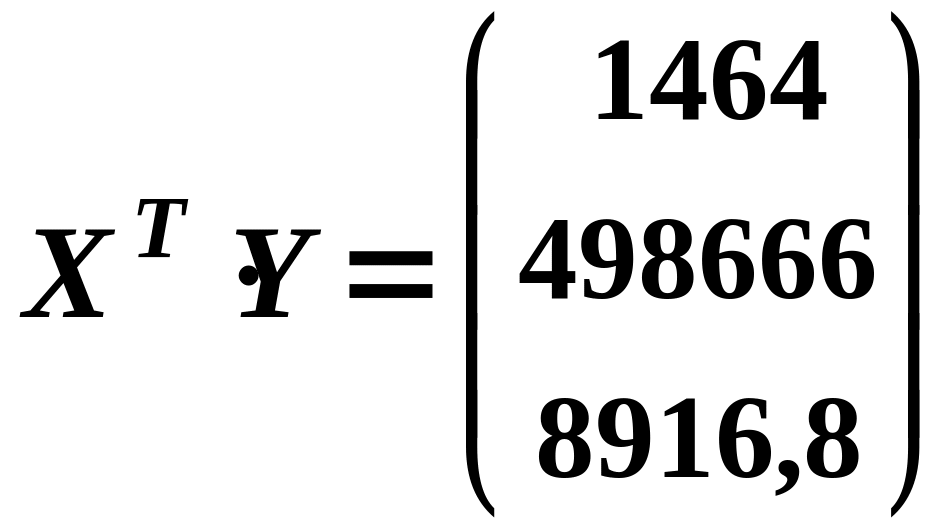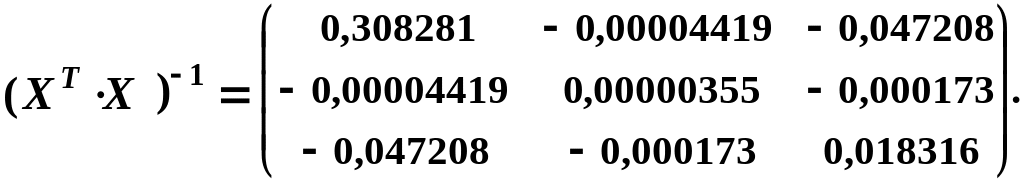
Множимо матрицю помилок на добуток матриць і визначаємо оцінки параметрів моделі:

;

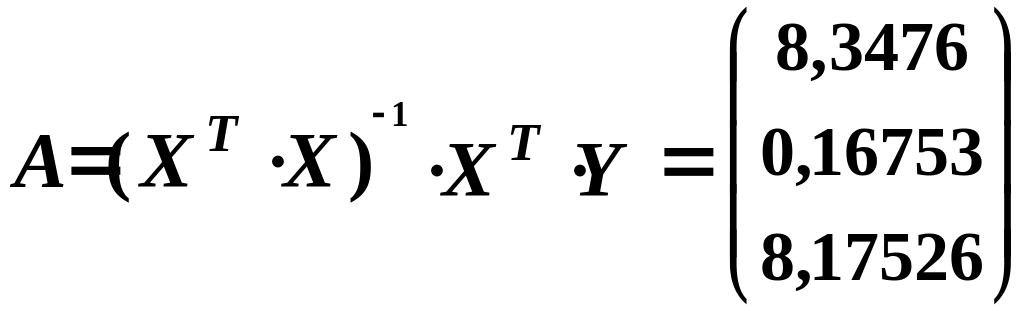Таким чином,

Економетрична модель має вигляд:

.

4. Визначимо теоретичні значення залежної змінної на основі побудованої моделі, підставивши в неї значення незалежних змінних та . Потім віднімемо розраховані теоретичні значення від фактичних , в результаті отримаємо залишки: 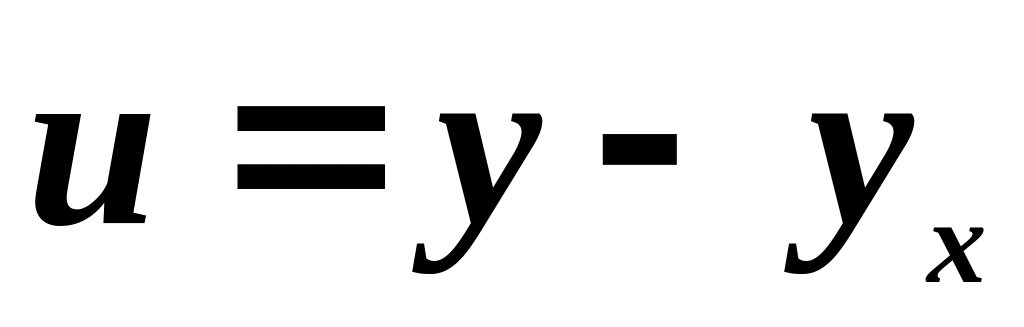. Всі ці розрахунки наведені в табл. 2.2.

Таблиця 2.2

Допоміжні розрахунки

№ п / п
1	20	28,14932	66,41143	5112,25
2	32	33,99274	3,970996	3540,25
3	48	44,82179	10,10099	1892,25

Таблиця 2.2 (продовження)

4	65	60,42217	20,9565	702,25
5	45	51,5562	42,98381	2162,25
6	64	62,23786	3,105151	756,25
7	79	74,99023	16,07825	156,25
8	104	113,2871	86,25077	156,25
9	68	75,11049	50,55913	552,25
10	93	89,01545	15,8766	2,25
11	117	107,1288	97,44104	650,25
12	145	159,9268	222,8098	2862,25
13	91	105,5199	210,8283	0,25
14	131	108,9108	487,9343	1560,25
15	167	146,4309	423,0898	5700,25
16	195	202,4995	56,24198	10712,25
Сума	1464	1464	1814,639	36518,000

5. Розрахуємо незміщені дисперсії залишків та залежної змінної :

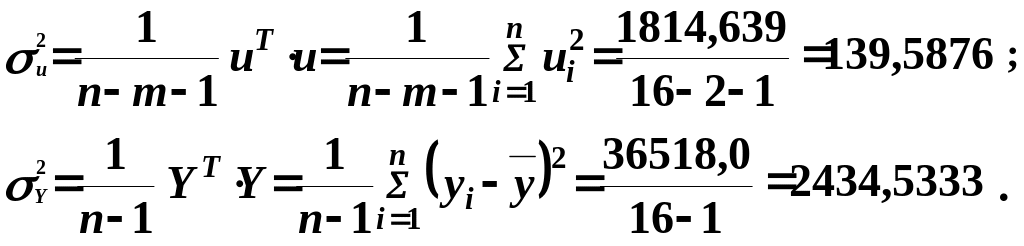
6. Визначимо матрицю коваріацій оцінок параметрів моделі (коваріаційну матрицю):

Діагональні елементи цієї матриці характеризують дисперсії оцінок параметрів моделі:

7. Знайдемо стандартні помилки оцінок параметрів:

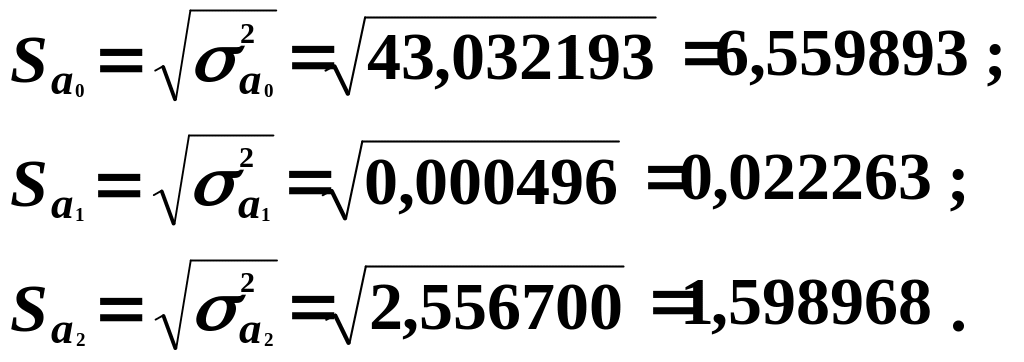
Порівняємо стандартні помилки оцінок параметрів моделі з величиною оцінки:

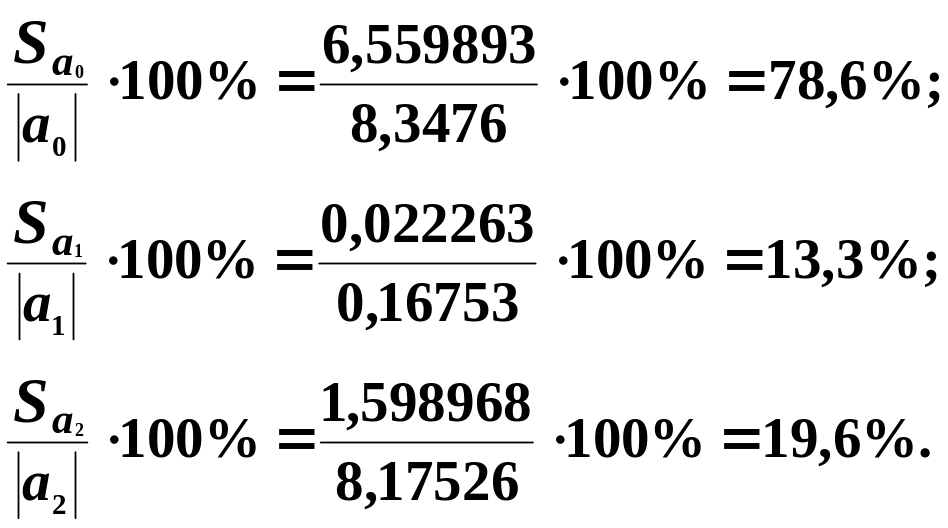
Співвідношення стандартної помилки й абсолютного значення параметра становить 78,6% , параметра — 13,3%, параметра — 19,6%. Перше співвідношення (воно більше 30%) свідчить про те, що оцінка параметра моделі може мати зміщення, а друге та третє співвідношення підтверджує незміщеність оцінок параметрів та .

8. Дамо змістовне тлумачення параметрів моделі

.

Оцінка параметра характеризує граничну зміну величини витрат на харчування залежно від зміни загальних затрат на одиницю. Тобто, якщо загальні затрати сім’ї зростуть на 1 тис. грн., то витрати на харчування в них збільшаться на 0,16753 тис. грн. при незмінному складі сім’ї.

Оцінка параметра характеризує граничне зростання витрат на харчування при збільшенні сім’ї на одного члена. Так, якщо склад сім’ї збагатиться ще одним членом, то витрати на харчування зростуть на 8,17526 тис. грн. при незмінній величині доходу.