1.2. Побудова та аналіз однофакторної економетричної моделі
Приклад 1.1. На основі даних про роздрібний товарообіг і доходи населення у деякому населеному пункті за 10 років побудувати економетричну модель роздрібного товарообігу. Дати загальну характеристику достовірності моделі та зробити висновки.
Вихідні дані та елементарні перетворення цих даних для побудови моделі наведені в табл. 1.2.
Таблиця 1.2
Вихідні дані
№ п/п |
|
|
|
|
|
|
|
1 |
17 |
18 |
324 |
306 |
16,68 |
0,102 |
25 |
2 |
18 |
20 |
400 |
360 |
18,32 |
0,1 |
16 |
3 |
19 |
21 |
441 |
399 |
19,14 |
0,018 |
9 |
4 |
20 |
22 |
484 |
440 |
19,95 |
0,002 |
4 |
5 |
21 |
24 |
576 |
504 |
21,59 |
0,349 |
1 |
6 |
23 |
25 |
625 |
575 |
22,41 |
0,349 |
1 |
7 |
24 |
27 |
729 |
648 |
24,05 |
0,002 |
4 |
8 |
25 |
28 |
784 |
700 |
24,86 |
0,018 |
9 |
9 |
26 |
29 |
841 |
754 |
25,68 |
0,1 |
16 |
10 |
27 |
31 |
961 |
837 |
27,32 |
0,102 |
25 |
Сума |
220 |
245 |
6165 |
5523 |
220 |
1,145 |
110 |
Розв’язання:
1. Ідентифікуємо змінні: – роздрібний товарообіг (залежна змінна); – доходи населення (незалежна змінна).
2. Нехай
специфікація моделі
визначається лінійною функцією; вона
має такий вигляд:
,
де
–– параметри моделі;
–– стохастична складова, залишки.
3. Оцінимо
параметри моделі
за методом 1МНК. Для цього запишемо
систему нормальних рівнянь:
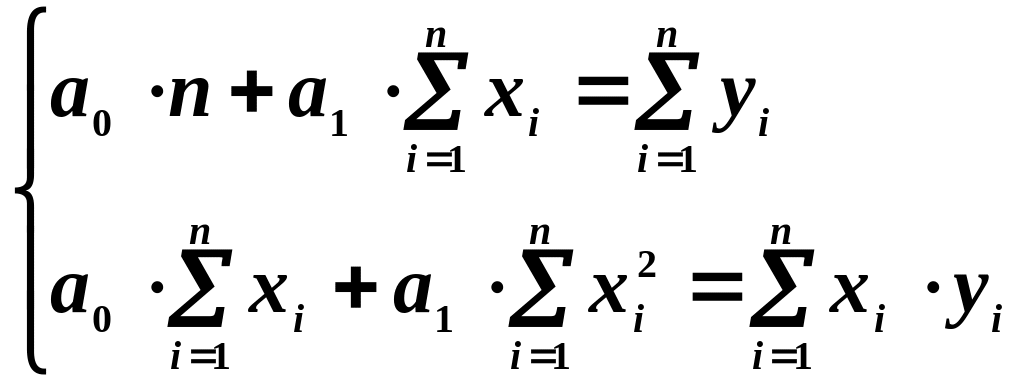
–– кількість спостережень.
Підставимо в цю систему
величини
,
які розраховані на основі вихідних
даних табл. 1.1; тоді система набуде такого
вигляду:
Розв’яжемо цю систему відносно невідомих параметрів :
.
Таким чином, економетрична модель запишеться так:
.
4. Розрахуємо дисперсії залежної змінної та залишків:
5. Визначимо коефіцієнти детермінації та кореляції:
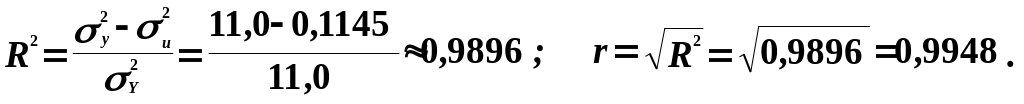
Оскільки коефіцієнт детермінації
,
це свідчить, що варіація обсягу роздрібного
товарообігу на 98,96%
визначається варіацією
доходів населення. Коефіцієнт кореляції
характеризує тісний зв’язок між цими
соціально-економічними показниками.
Величини R2
і r для однофакторної
економетричної моделі свідчать про її
достовірність, якщо вони наближаються
до одиниці.
6. Знайдемо матрицю помилок C (матрицю, обернену до матриці системи нормальних рівнянь):
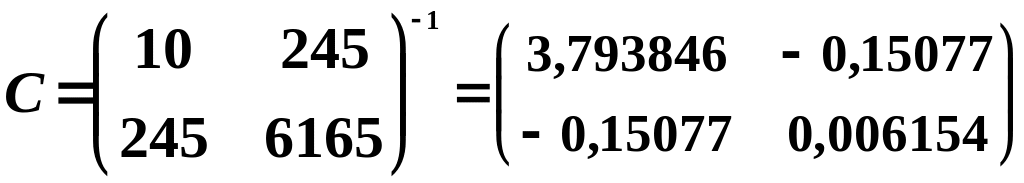
7. Визначимо стандартні помилки оцінок параметрів моделі, враховуючи дисперсію залишків:
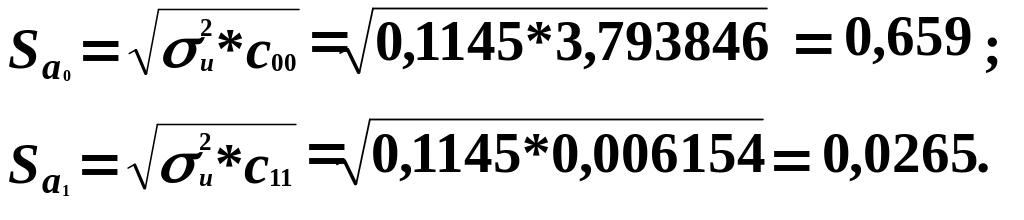
Порівняємо стандартні помилки оцінок параметрів моделі з величиною цих оцінок.
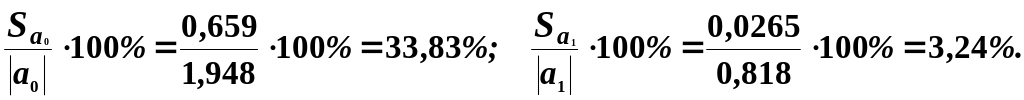
У теорії економетричних
досліджень прийнято вважати, що оцінка
параметру моделі є незміщеною, якщо
відношення стандартної помилки оцінки
до її абсолютної величини не перевищує
30 відсотків. В результаті визначимо, що
стандартна помилка оцінки параметру
становить 3,24%
абсолютного значення цієї оцінки
(0,818),
що свідчить про незміщеність даної
оцінки параметру моделі. Стандартна
помилка оцінки параметру
становить 33,83%
абсолютного значення цієї оцінки
(1,948), а
це означає, що даний параметр може мати
зміщення, яке зумовлюється невеликою
сукупністю спостережень (n
= 10).
Висновки. Економетрична модель кількісно описує зв’язок роздрібного товарообігу і доходів населення.
Параметр
характеризує граничну величину витрат
на купівлю товарів у роздрібній торгівлі,
коли дохід збільшується на одиницю,
тобто при збільшенні доходів на одиницю
обсяг роздрібного товарообігу зростає
на 0,818
одиниці
.
Визначимо коефіцієнт еластичності роздрібного товарообігу залежно від доходів населення:
.
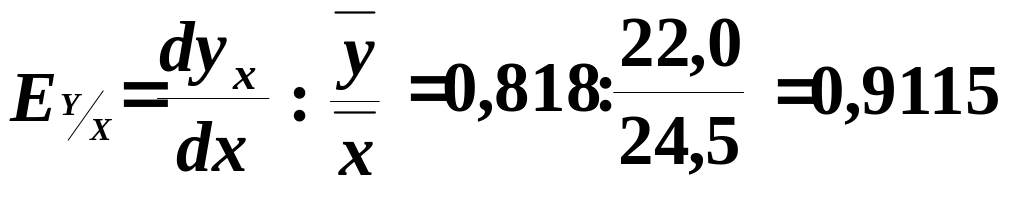На основі коефіцієнта еластичності можна стверджувати, що при збільшенні доходів населення на один процент роздрібний товарообіг зросте на 0,9115%.
Приклад 1.2. На основі даних про відвідування занять школярами та їх успішність у школах м. Чернігова побудувати економетричні моделі витрат на харчування: лінійну, параболічну, показникову. За принципом мінімальності незміщеного стандартного відхилення вибрати найбільш адекватну економетричну модель.
Таблиця 1.3
Дані до задачі
№ п/п |
Відсоток відвіданих школярем уроків, % |
Середній рівень знань школяра, балів |
1 |
65,0 |
4,50 |
2 |
67,5 |
4,70 |
3 |
70,0 |
4,85 |
4 |
72,5 |
5,25 |
5 |
75,0 |
5,75 |
6 |
77,5 |
6,25 |
7 |
80,0 |
6,45 |
8 |
82,5 |
6,85 |
9 |
85,0 |
7,30 |
10 |
87,5 |
8,10 |
11 |
90,0 |
8,75 |
12 |
92,5 |
9,45 |
13 |
95,0 |
10,20 |
14 |
97,5 |
10,85 |
15 |
100,0 |
11,25 |
Розв’язання:
Ідентифікуємо змінні: – середній рівень знань (залежна змінна); – відсоток відвіданих уроків (незалежна змінна).
Побудуємо емпіричний точковий графік.
Рисунок 1.1 – Емпіричний точковий графік (діаграма розсіяння)
Аналізуючи рисунок 1.1, зробимо висновок, що в якості аналітичної залежності можна обрати одну з наступних функцій:
лінійну:
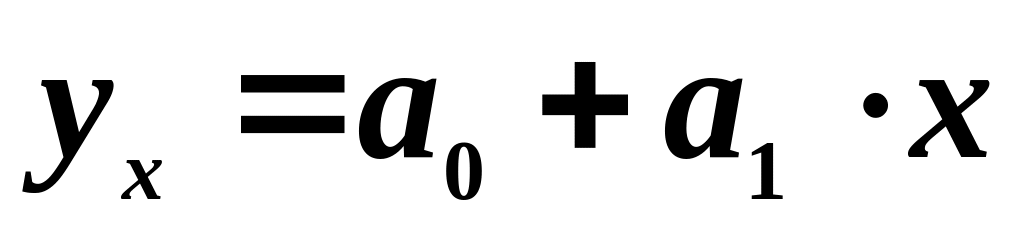;параболу другого порядку
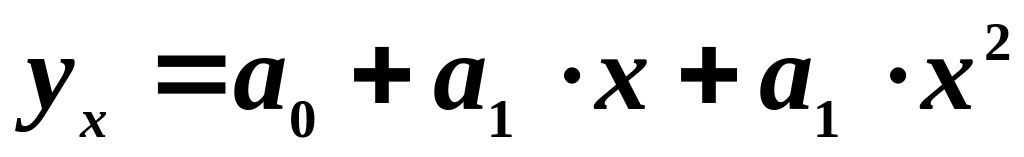;показову:
.
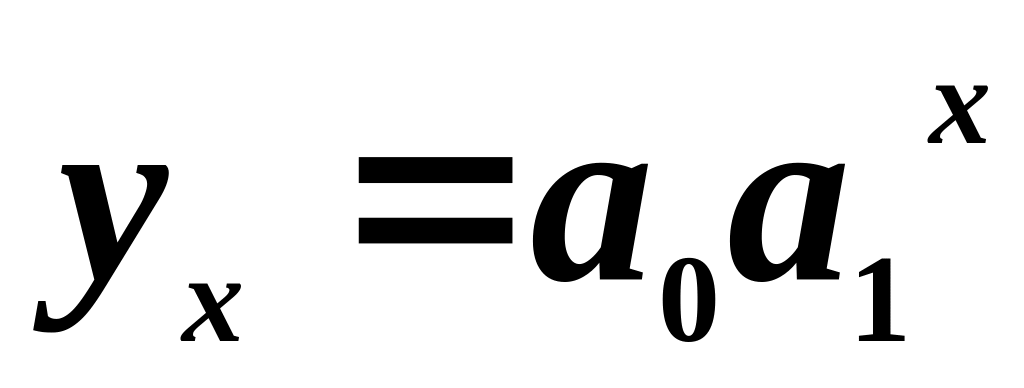Застосуємо метод МНК для визначення параметрів рівняння регресії.
Для лінійної моделі система
нормальних рівнянь має вигляд (
–– кількість спостережень):
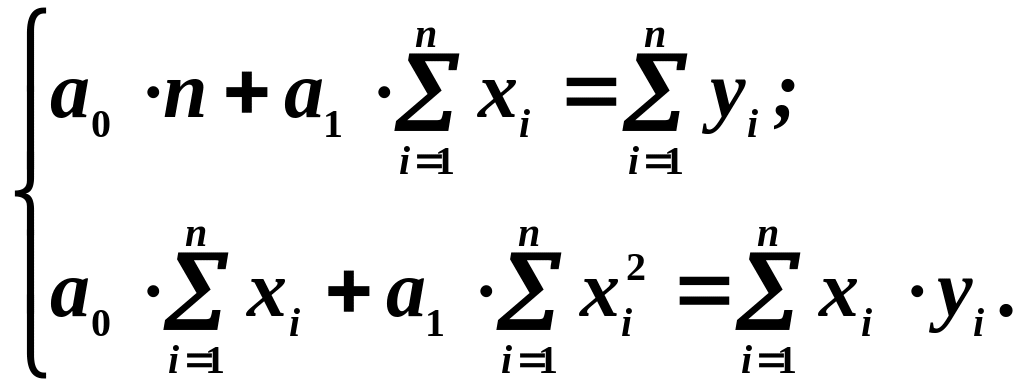(1.1)
Для параболи другого порядку: система нормальних рівнянь має вигляд:
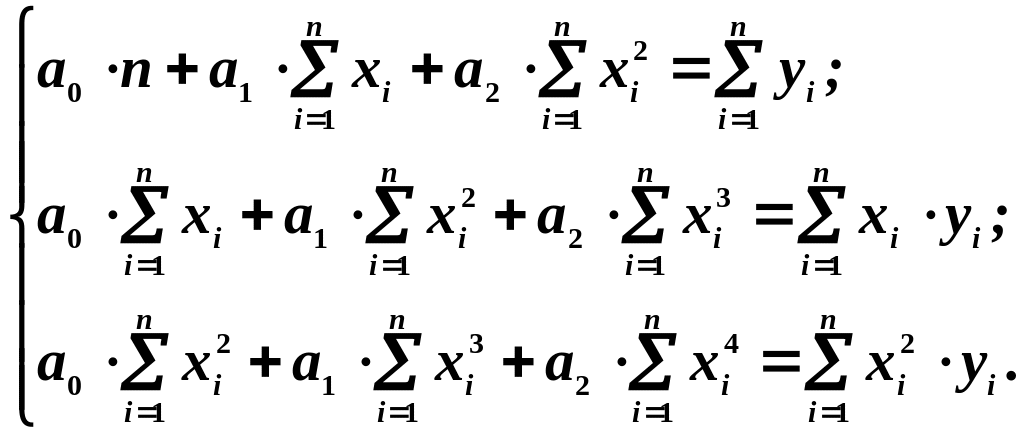(1.2)
Для знаходження параметрів показової моделі застосуємо прийом, який в економетрії носить назву лінеаризація.
Логарифмуємо обидві частини рівності . Отримаємо:
.
Остання формула задає лінійну
залежність
від змінної
.
Отже, система нормальних рівнянь для показової функції має вигляд:
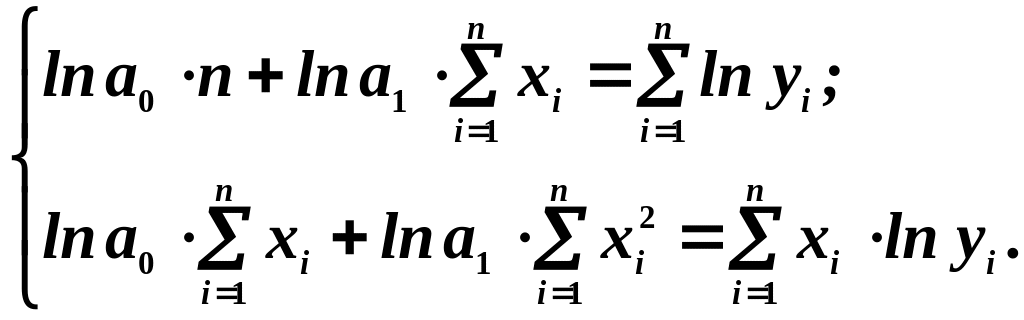(1.3)
Складемо розрахункову таблицю для обчислення коефіцієнтів систем нормальних рівнянь (1.1) – (1.3) (таблиця 1.4).
Таблиця 1.4
Розрахункова таблиця для обчислення коефіцієнтів систем нормальних рівнянь
№ п/п |
|
|
|
|
|
|
|
|
|
1 |
65 |
4,5 |
4225 |
274625 |
17850625 |
292,5 |
19012,5 |
1,5040774 |
97,76503079 |
2 |
67,5 |
4,7 |
4556,25 |
307546,88 |
20759414,1 |
317,25 |
21414,375 |
1,54756251 |
104,4604693 |
3 |
70 |
4,85 |
4900 |
343000 |
24010000 |
339,5 |
23765 |
1,5789787 |
110,5285093 |
4 |
72,5 |
5,25 |
5256,25 |
381078,13 |
27628164,1 |
380,625 |
27595,3125 |
1,65822808 |
120,2215356 |
5 |
75 |
5,75 |
5625 |
421875 |
31640625 |
431,25 |
32343,75 |
1,74919985 |
131,1899891 |
6 |
77,5 |
6,25 |
6006,25 |
465484,38 |
36075039,1 |
484,375 |
37539,0625 |
1,83258146 |
142,0250634 |
7 |
80 |
6,45 |
6400 |
512000 |
40960000 |
516 |
41280 |
1,86408013 |
149,1264105 |
8 |
82,5 |
6,85 |
6806,25 |
561515,63 |
46325039,1 |
565,125 |
46622,8125 |
1,92424865 |
158,7505138 |
9 |
85 |
7,3 |
7225 |
614125 |
52200625 |
620,5 |
52742,5 |
1,98787435 |
168,9693196 |
10 |
87,5 |
8,1 |
7656,25 |
669921,88 |
58618164,1 |
708,75 |
62015,625 |
2,09186406 |
183,0381054 |
11 |
90 |
8,75 |
8100 |
729000 |
65610000 |
787,5 |
70875 |
2,1690537 |
195,214833 |
12 |
92,5 |
9,45 |
8556,25 |
791453,13 |
73209414,1 |
874,125 |
80856,5625 |
2,24601474 |
207,7563636 |
13 |
95 |
10,2 |
9025 |
857375 |
81450625 |
969 |
92055 |
2,32238772 |
220,6268334 |
14 |
97,5 |
10,85 |
9506,25 |
926859,38 |
90368789,1 |
1057,875 |
103142,8125 |
2,38416508 |
232,4560953 |
15 |
100 |
11,25 |
10000 |
1000000 |
100000000 |
1125 |
112500 |
2,42036813 |
242,0368129 |
Сума |
1237,5 |
110,5 |
103843,75 |
8855859,375 |
766706523,4 |
9469,375 |
823760,3125 |
29,2806846 |
2464,165885 |
Підставляємо розраховані коефіцієнти у системи нормальних рівнянь:
для лінійної моделі:
для параболічної моделі:
для показової моделі:
Розв’язуючи ці системи рівнянь, знаходимо параметри рівнянь регресії (таблиця 1.5).
Таблиця 1.5
Параметри рівнянь регресії
Лінійна функція |
Парабола 2-го порядку |
Показова функція |
|||
a0= |
-9,28065 |
a0= |
11,990231 |
а0= |
0,7154622 |
a1= |
0,2017857 |
a1= |
-0,322865 |
а1= |
1,0281074 |
|
|
a2= |
0,0031797 |
|
|
Маємо моделі:
лінійна модель:
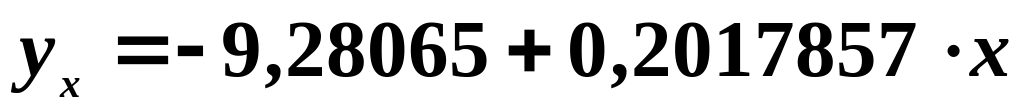;парабола 2-го порядку:
.показова модель:
.
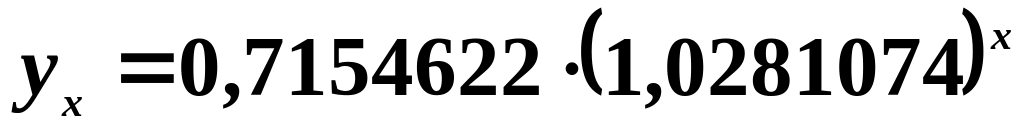Розрахуємо теоретичні рівні по кожній моделі, а також квадрати залишків та їх суми (табл.. 1.6).
Таблиця 1.6
Розрахунок стандартних помилок апроксимації
№ п/п |
|
Лінійна модель |
Параболічна модель |
Показова модель |
|||
|
|
|
|
|
|
||
1 |
4,5 |
3,835417 |
0,441671 |
4,4382353 |
0,003815 |
4,335997 |
0,0269 |
2 |
4,7 |
4,339881 |
0,1296857 |
4,6843487 |
0,000245 |
4,647134 |
0,00279 |
3 |
4,85 |
4,844345 |
3,198E-05 |
4,9702085 |
0,01445 |
4,980598 |
0,01706 |
4 |
5,25 |
5,34881 |
0,0097633 |
5,2958145 |
0,002099 |
5,337989 |
0,00774 |
5 |
5,75 |
5,853274 |
0,0106655 |
5,6611668 |
0,007891 |
5,721026 |
0,00084 |
6 |
6,25 |
6,357738 |
0,0116075 |
6,0662654 |
0,033758 |
6,131549 |
0,01403 |
7 |
6,45 |
6,862202 |
0,1699108 |
6,5111102 |
0,003734 |
6,571529 |
0,01477 |
8 |
6,85 |
7,366667 |
0,2669444 |
6,9957014 |
0,021229 |
7,04308 |
0,03728 |
9 |
7,3 |
7,871131 |
0,3261906 |
7,5200388 |
0,048417 |
7,548469 |
0,06174 |
10 |
8,1 |
8,375595 |
0,0759527 |
8,0841225 |
0,000252 |
8,090123 |
9,8E-05 |
11 |
8,75 |
8,88006 |
0,0169155 |
8,6879525 |
0,00385 |
8,670644 |
0,0063 |
12 |
9,45 |
9,384524 |
0,0042871 |
9,3315288 |
0,014035 |
9,292822 |
0,0247 |
13 |
10,2 |
9,888988 |
0,0967284 |
10,014851 |
0,03428 |
9,959645 |
0,05777 |
14 |
10,85 |
10,39345 |
0,2084357 |
10,73792 |
0,012562 |
10,67432 |
0,03086 |
15 |
11,25 |
10,89792 |
0,1239627 |
11,500735 |
0,062868 |
11,44027 |
0,0362 |
Сума |
110,5 |
110,5 |
1,892753 |
110,5 |
0,263487 |
110,5 |
0,33908 |
|
|
0,355223 |
|
0,132536 |
|
0,150352 |
|
У
останньому рядку таблиці для кожного
з трьох рівнянь розрахована стандартна
похибка апроксимації:
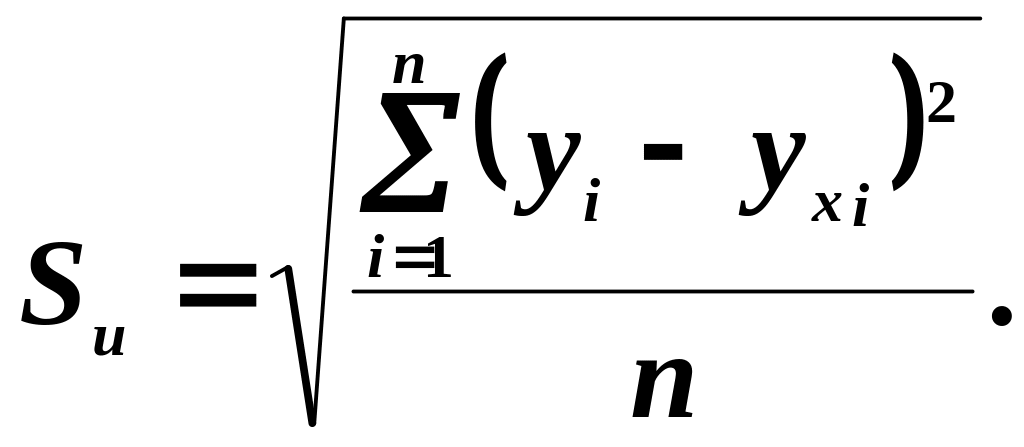
Отримані значення стандартної похибки апроксимації є досить низькими, що свідчить про правильність обраного типу залежності та високу достовірність розрахованих коефіцієнтів.
Найменшою є похибка, розрахована для параболічної моделі, тому ця модель є більш достовірною.
Будуємо лінію регресії (графік параболічної моделі) на кореляційному полі.
Рисунок 1.2. – Лінія регресії на кореляційному полі
Висновок:
Таким чином, за результатами проведених розрахунків, адекватною моделлю визнана параболічна функція, яка дає найменші похибки.