Завдання для самостійного виконання

Використовуючи самостійно сформовані дані, виконати приклади, наведені у лабораторній роботі. Звіт оформити у відповідності зі зразком.

Лабораторна робота 1 Тема: Побудова однофакторної економетричної моделі Мета: набути навички побудови однофакторної економетричної моделі та її дослідження засобами ms excel

Завдання 1. На основі даних про роздрібний товарообіг і доходи населення у деякому населеному пункті за 10 років побудувати економетричну модель роздрібного товарообігу. Дати загальну характеристику достовірності моделі та зробити висновки.

Вихідні дані наведені в табл. 1.1.

Таблиця 1.1

Вихідні дані до задачі

N п/п	Роздрібний товарообіг, млн.. грн.	Доходи населення, млн.. грн.
1	17	18
2	18	20
3	19	21
4	20	22
5	21	24
6	23	25
7	24	27
8	25	28
9	26	29
10	27	31

Виконання завдання:

Ідентифікуємо змінні: – роздрібний товарообіг (залежна змінна); – доходи населення (незалежна змінна).

Завантажуємо програму MS EXCEL. За допомогою буферу обміну переносимо дані таблиці 1.1 на аркуш (дамо аркушу назву «Завдання 1») MS EXCEL:

Рисунок 1.1 – Дані до задачі

Для вибору форми залежності між показниками та побудуємо емпіричний точковий графік:

Рисунок 1.2 – Емпіричний точковий графік

Як видно з результатів побудови, усі точки розташовані обіруч деякої уявної прямої. Тому у якості економетричної моделі можна обрати лінійну функцію:

,

де –– параметри моделі.

Оцінимо параметри моделі за методом 1МНК. Для цього складемо розрахункову таблицю.

У рядку 1 аркуша MS EXCEL записуємо заголовки стовпчиків: у комірці D1 записуємо «Х**2», у комірці Е1 записуємо «Х*Y», у комірці F1 записуємо «Y(x)», у комірці G1 записуємо «u**2», у комірці Н1 записуємо «(Y-Y(cp))**2». У комірці А12 робимо запис «Сума» – у рядку 12 будуть обчислюватися суми відповідних стовпчиків.

Розташовуємо курсор у комірці D2. Набираємо команду «=С2*С2» та натискаємо <Enter>. Використовуючи АВТОЗАПОВНЕННЯ, виконуємо аналогічні обчислення у комірках D3:D11.

Розташовуємо курсор у комірці Е2. Набираємо команду «=С2*В2» та натискаємо <Enter>. Використовуючи АВТОЗАПОВНЕННЯ, виконуємо аналогічні обчислення у комірках Е3:Е11.

Розташовуємо курсор у комірці В12. Натискаємо піктограму АВТОСУМА, або набираємо команду «=СУММ(B2:B11)» та натискаємо <Enter>. Використовуючи АВТОЗАПОВНЕННЯ, виконуємо аналогічні обчислення у комірках С12:Н12. Результати представлено на рис. 1.3.

Об’єднаємо комірки В14:D14 та запишемо в них заголовок «Система нормальних рівнянь». Нагадаємо, що така система для лінійної моделі має вид:

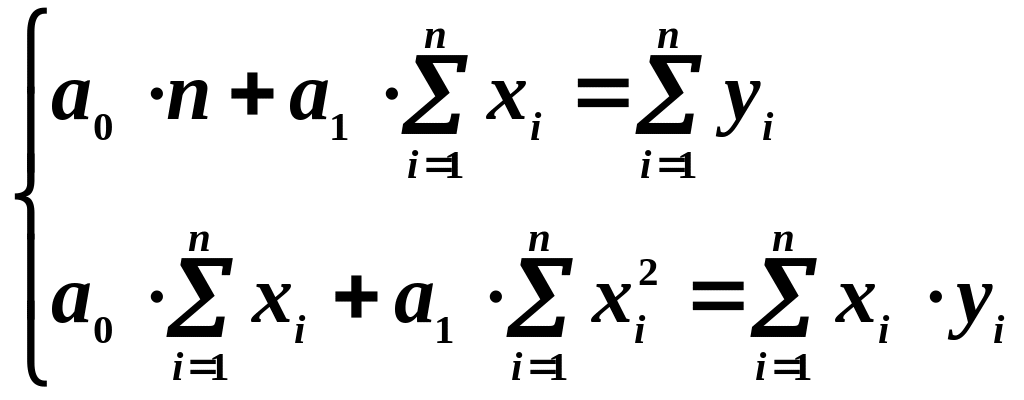
У комірку В15 запишемо число 10 – кількість спостережень.

Рисунок 1.3 – Розрахунок коефіцієнтів системи нормальних рівнянь

Комірка С15 повинна бути заповнена сумою значень незалежної змінної . Ця сума раніше обчислена у комірці С12. Тому розташуємо курсор у комірці С15, набираємо «=», клацаємо лівою кнопкою миші на комірці С12 та натискаємо <Enter>. Теж саме робимо у комірці В16.

Комірка С16 повинна бути заповненою сумою квадратів значень незалежної змінної . Ця сума раніше обчислена у комірці D12. Тому розташуємо курсор у комірці С16, набираємо «=», клацаємо на комірці D12 та натискаємо <Enter>.

Аналогічно у комірки D15 та D16 заносимо вміст комірок В12 (сума ) та Е12 (сума ) відповідно.

У комірках F15 та F16 записуємо заголовки «А0=» та «А1=» відповідно.

Розрахунок цих оцінок параметрів лінійної моделі здійснюємо у комірках G15:G16.

Для цього розташовуємо курсор у комірці G15. Розв’язуємо систему нормальних рівнянь методом оберненої матриці (матричним методом). Набираємо команду «=МУМНОЖ(МОБР(B15:C16);D15:D16)» та натискаємо <Enter>. Виділяємо комірки G15:G16, натискаємо F2, потім одночасно натискаємо клавіші <Ctrl>+<Shift>+<Enter>.

Рисунок 1.4 – Розрахунок параметрів лінійної економетричної моделі

Маємо: .

Таким чином, економетрична модель запишеться так: .

У комірках стовпчика F розрахуємо теоретичні значення результативного показника. Для цього у комірці F2 набираємо команду «=$G$15+$G$16*C2» та натискаємо <Enter>. Обчислення у комірках F3:F11 виконуємо шляхом автозаповнення.

У комірках стовпчика G обчислюємо квадрати залишків, які будуть використані для розрахунку дисперсії залишків. Для цього у комірці G2 набираємо команду «=(B2-F2)^2» та натискаємо <Enter>. Обчислення у комірках G3:G11 виконуємо шляхом автозаповнення.

У комірках стовпчика Н виконуємо обчислення для розрахунку дисперсії залежної змінної. Для цього у комірці Н2 набираємо команду «=(B2-СРЗНАЧ(B$2:B$11))^2» та натискаємо <Enter>. Обчислення у комірках Н3:Н11 виконуємо шляхом автозаповнення.

Об’єднуємо комірки А18:D18 та записуємо в них заголовок «Дисперсія залишків =». У комірці Е18 обчислюємо цю дисперсію: набираємо команду «=G12/10».

Об’єднуємо комірки А19:D19 та записуємо в них заголовок «Дисперсія залежної змінної =». У комірці Е19 обчислюємо цю дисперсію: набираємо команду «=H12/10».

Об’єднуємо комірки А20:D20 та записуємо в них заголовок «Коефіцієнт детермінації = ». У комірці Е20 обчислюємо цей коефіцієнт: набираємо команду «=(E19-E18)/E19».

Об’єднуємо комірки А21:D21 та записуємо в них заголовок «Коефіцієнт кореляціїї = ». У комірці Е21 обчислюємо цей коефіцієнт: набираємо команду «=КОРЕНЬ(E20)».

Рисунок 1.5 – Результати розрахунків

Знаходимо матрицю помилок. Об’єднуємо комірки Н18:І18 та записуємо у цих комірках заголовок «Матриця помилок». У комірці Н19 набираємо команду «=МОБР(B15:C16)» та натискаємо <Enter>. Виділяємо комірки Н19:І20, натискаємо F2, потім одночасно натискаємо клавіші <Ctrl>+<Shift>+<Enter>.

Рисунок 1.6 – Матриця помилок

Визначимо стандартні помилки оцінок параметрів моделі.

Об’єднуємо комірки А22:С23, записуємо заголовок «Стандартні помилки оцінок параметрів моделі». У комірках D22 та D23 записуємо заголовки «Sa(0)=» та «Sa(1)=» відповідно.

У комірці Е22 набираємо команду «=КОРЕНЬ(E18*H19)». У комірці Е23 набираємо команду «=КОРЕНЬ(E18*I20)».

Рисунок 1.7 – Стандартні помилки оцінок параметрів моделі

Порівняємо стандартні помилки оцінок параметрів моделі з величиною цих оцінок. Для цього обчислимо відношення цих помилок до модулів оцінок.

Об’єднуємо комірки А24:С25, записуємо заголовок «Відношення помилок до модулів оцінок». У комірках D24 та D24 записуємо заголовки «a(0)» та «a(1)» відповідно.

У комірці Е24 набираємо команду «=E22/ABS(G15)*100». У комірці Е25 набираємо команду «=E23/ABS(G16)*100».

Рисунок 1.8 – Перевірка незміщеності оцінок параметрів моделі

Визначимо коефіцієнт еластичності роздрібного товарообігу залежно від доходів населення. Об’єднуємо комірки А26:D26, записуємо заголовок «Коефіцієнт еластичності=». У комірці Е26 набираємо команду «=G16*C12/B12».

Рисунок 1.8 – Розрахунок коефіцієнта еластичності

Результати усіх описаних вище розрахунків представлені на рисунку 1.9.

Рисунок 1.9 – Результати усіх розрахунків

Висновки:

У ході виконання лабораторної роботи була побудована лінійна однофакторна економетрична модель , яка кількісно описує залежність роздрібного товарообігу від доходів населення.

Параметр характеризує граничну величину витрат на купівлю товарів у роздрібній торгівлі. При збільшенні доходу на 1 млн. грн. обсяг роздрібного товарообігу зростає на 0,818 млн. грн.

Параметр характеризує обсяг роздрібного товарообігу при відсутності доходів населення. Можна говорити про те, що населення міста купуватимемо товари за рахунок накопичених раніше заощаджень.

Оскільки коефіцієнт детермінації , це свідчить, що варіація обсягу роздрібного товарообігу на 98,96% визначається варіацією доходів населення. Коефіцієнт кореляції вказує на те, що обсяг роздрібного товарообігу на 99,48% залежить від обсягу доходів населення. Близькість коефіцієнту кореляції до одиниці свідчить про тісний зв’язок між цими соціально-економічними показниками.

У теорії економетричних досліджень прийнято вважати, що оцінка параметру моделі є незміщеною, якщо відношення стандартної помилки оцінки до її абсолютної величини не перевищує 30 відсотків. В результаті дослідження встановлено, що стандартна помилка оцінки параметру становить 3,24% абсолютного значення цієї оцінки (0,818), що свідчить про незміщеність даної оцінки параметру моделі. Стандартна помилка оцінки параметру становить 33,8% абсолютного значення цієї оцінки (1,948), а це означає, що даний параметр може мати зміщення, яке зумовлюється невеликою сукупністю спостережень (n = 10). На основі розрахованого коефіцієнта еластичності можна стверджувати, що при збільшенні доходів населення на один процент роздрібний товарообіг зросте на 0,91%.