Використання нелінійних функцій у економетрії

У багатьох випадках припущення щодо лінійної залежності між певними показниками економічного явища чи процесу може не підтверджуватися даними спостережень цих показників. Тому розглянемо в якості нелінійних функцій експоненціальні функції та наведемо приклади їх використання в економетричному аналізі.

Квадратична вирівнювальна функція

Нерідко може статися так, що емпіричні (експериментальні) дані розташовуються вздовж лінії, яка зовсім не нагадує пряму. Тоді для вирівнювання обирається інша, складніша функція.

Приклад 2. Спостерігаючи за спортсменом-спринтером на протязі півроку, вдалося зібрати дані про його спортивні результати в залежності від тривалості тренувань. Тут - час (секунд), показаний спортсменам під час контрольного забігу на стометрівці; - середня тривалість (годин) щоденного тренування у передстартовому періоді (2–2,5 тижнів). Результати спостережень відображені в наступній таблиці 3. Побудуємо точковий графік (рис. 2).

Якщо ми на роль рівняння регресії візьмемо лінійне рівняння (1), то навряд чи така функція принесе нам практичну користь. Адже розташування експериментальних точок на графіку зовсім не схоже на пряму лінію, а більше нагадує квадратичну параболу (графік многочлена другого степеня). Тому рівняння регресії будуватимемо у вигляді:

(3).

Таблиця 3

Дані до задачі

№ п/п	Тривалість тренування, годин	Результат забігу, секунд
1	0,5	12,5
2	1,0	11,2
3	1,5	10,6
4	2,0	10,4
5	2,5	10,3
6	3,0	10,25
7	3,5	10,35
8	4,0	10,7
9	4,5	11,2
10	5,0	13,6

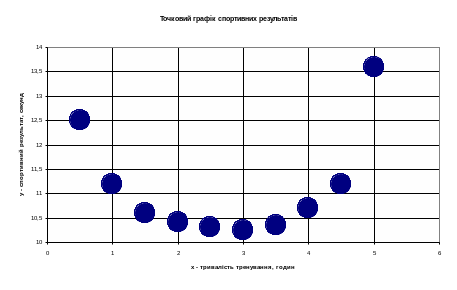
Рисунок 2 – Емпіричний точковий графік спортивних результатів

У відповідності з МНК отримаємо систему трьох лінійних рівнянь з трьома невідомими :

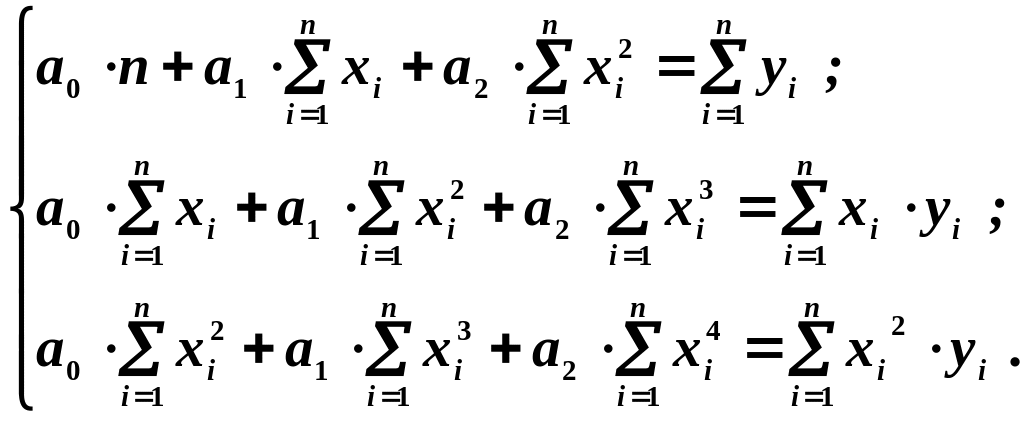(4).

- кількість спостережень.

Обчислимо коефіцієнти цієї системи рівнянь (таблиця 4).

Таблиця 4

Розрахункова таблиця коефіцієнтів системи нормальних рівнянь

1	0,5	12,50	0,25	0,125	0,0625	6,250	3,1250	12,45
2	1,0	11,20	1,00	1,000	1,0000	11,200	11,2000	11,43
3	1,5	10,60	2,25	3,375	5,0625	15,900	23,8500	10,69
4	2,0	10,40	4,00	8,000	16,0000	20,800	41,6000	10,21
5	2,5	10,30	6,25	15,625	39,0625	25,750	64,3750	10,00
6	3,0	10,25	9,00	27,000	81,0000	30,750	92,2500	10,06
7	3,5	10,35	12,25	42,875	150,0625	36,225	126,7875	10,39
8	4,0	10,70	16,00	64,000	256,0000	42,800	171,2000	10,99
9	4,5	11,20	20,25	91,125	410,0625	50,400	226,8000	11,87
10	5,0	13,60	25,00	125,000	625,0000	68,000	340,0000	13,01
Сума	27,5	111,10	96,25	378,125	1583,3125	308,075	1101,1875	111,10

Маємо:

Розв’язуючи цю систему рівнянь, знаходимо оцінки параметрів економетричної моделі:

Рівняння регресії:

(5)

У останньому стовпчику таблиці 4 обчислені теоретичні значення результатів спортсмена (значення вирівнювальної функції при відповідних значеннях незалежної змінної ).

Для наочності побудуємо (рис. 3) в одній системі координат графік функції (5) та емпіричний точковий графік.

Функцію (5) можна використовувати для підвищення ефективності планування тренувального процесу. Так, наприклад, за її допомогою можна обчислити оптимальну тривалість тренування та ряд інших важливих показників.

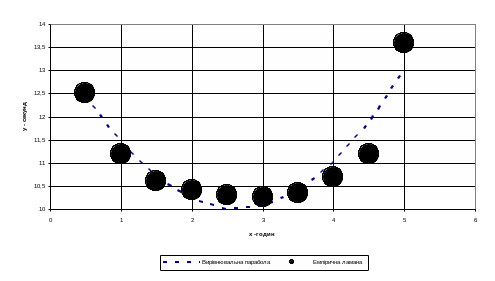
Рисунок 3 – Лінія регресії на кореляційному полі