Контрольні запитання

1. Які основні причини використання систем одночасних рівнянь?

2. У чому полягає основна розбіжність між структурними рівнян­нями системи і рівняннями у зведеній формі?

3. Чому звичайний МНК практично не використовується для оці­нювання систем одночасних рівнянь?

4. У чому полягає суть непрямого методу найменших квад­ратів?

5. Яка проблема часто виникає в процесі чисельного оцінюван­ня параметрів структурних рівнянь за оцінками коефіцієнтів зведе­них рівнянь?

6. Назвіть причини неідентифікованості й надідентифікованості систем структурних рівнянь.

7. Наведіть необхідні й достатні умови ідентифікованості систем.

8. Які системи можна оцінювати звичайним МНК?

9. У чому полягає суть двокрокового методу найменших квадратів (2МНК)?

10. Які з наступних тверджень є істинними, помилковими чи невизначеними? Відповідь поясніть.

а. Звичайний МНК незастосовний для оцінювання ко­ефіцієнтів структурних рівнянь систем одночасних рівнянь.

б. МНК рідко використовується для оцінювання коефіцієнтів структурних рівнянь систем одночасних рівнянь, тому що існують методи отримання більш якісних оцінок.

в. Екзогенні та визначені змінні моделі по суті одне й те саме.

г. Інструментальні змінні дають змогу розв'язати одну із серйозних проблем систем одночасних рівнянь — проблему корельованості пояснюючої змінної з випадковим відхиленням.

д. Проблема неідентифікованості передусім пов'язана з немож­ливістю отримання оцінок коефіцієнтів структурних рівнянь.

є. Не існує єдиного критерію для оцінювання загальної якості всієї системи одночасних рівнянь.

є. Якщо рівняння точно ідентифіковані, то оцінки, отримані за методом інструментальних змінних, і оцінки, отримані за 2МНК, бу­дуть ідентичні.

ж. Оцінки, отримані за 2МНК, мають бажані властивості лише при великих вибірках.

з. Для точно ідентифікованих систем 2МНК не використо­вується.

Комплект лабораторних робіт

Лабораторна робота (вступна)

Тема: Вивчення можливостей Майстра функцій ms excel

Мета: набути навички використання Майстра функцій ms excel при розв’язуванні економетричних задач

Завдання. Розв’язуючи наведені нижче приклади, вивчити наведені функції, які використовуються у економетричному моделюванні.

Виконання завдання:

Піктограма Майстра функцій (значок ) знаходиться у над робочим аркушем MS EXCEL (рис. 0.1).

Рисунок 0.1 – Місцезнаходження піктограми Майстра функцій

Вікно Майстра функцій відкривається (шаг 1 из 2), якщо натиснути лівою кнопкою миші на цю піктограму (рис. 0.2). Для пошуку та використання потрібної функції треба обрати категорію, до якої ця функція відноситься.

Рисунок 0.2 – Вікно Майстра функцій (шаг 1 из 2)

По кожній обраній функції можна отримати довідку (формат функції, приклади використання тощо).

Розглянемо приклади застосування деяких функцій.

Увага!! Набір команди для використання будь-якої функції з бібліотеки Майстра функцій завжди починається зі знака «=». Команди можна набирати як малими, так і великими літерами.

Функції категорії «Математические»

1. Функція «=EXP(число)» - повертає експоненту даного числа.

Приклад. У комірці А1 набираємо команду «=EXP(2,5)», отримаємо результат:

Рисунок 0.3

2. Функція «=LN(число)» - повертає логарифм натуральний даного числа.

3. Функція «=LOG(число;основа)» - повертає логарифм даного числа за даною основою.

Приклад. У комірці А2 набираємо команду «=LOG(32;2)», отримаємо результат: .

Рисунок 0.4

4. Функція «=СТЕПЕНЬ(число;степінь)» – повертає результат піднесення числа до степеня. Піднесення до степеня можна виконати в іншому форматі, шляхом набору команди «=число^степінь».

Функція «=КОРЕНЬ(число)» - повертає значення квадратного кореня з даного числа.

5. Функція «=МОБР(масив)» - повертає обернену матрицю (матриця зберігається у масиві).

Увага!! Якщо масив сформовано, то його частину змінювати не можна.

Приклад. У комірках діапазону С2:F5 записані елементи матриці

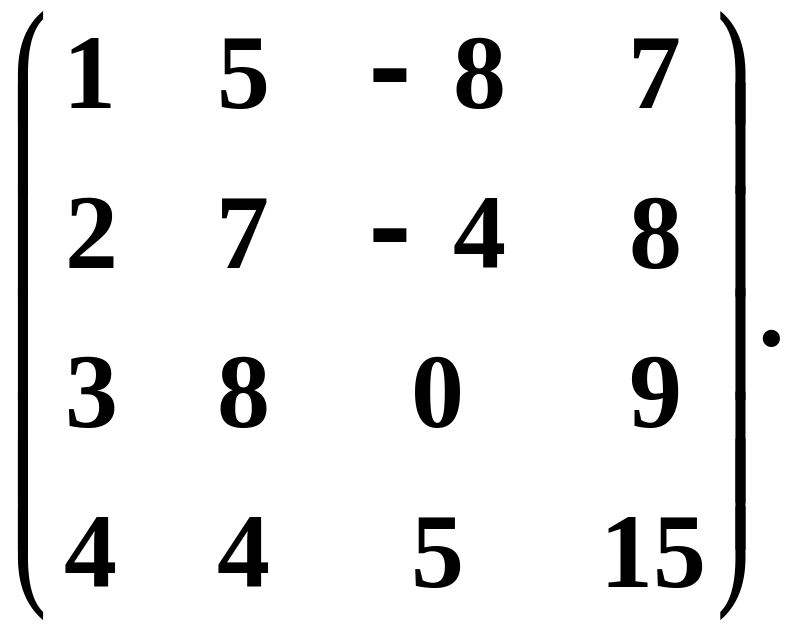
Потрібно знайти обернену матрицю.

Обернена матриця матиме такі ж розміри , як і початкова матриця. Отже, перш за все треба визначитися, у якому діапазоні комірок буде розташовуватися ця матриця. Обираємо, наприклад, діапазон комірок Н2:К5. У лівому верхньому кутку цього діапазону (у комірці Н2) набираємо команду «=МОБР(С2:F5)» та натискаємо <Enter>. Увага!! Якщо у тексті команди фігурує адреса комірки чи діапазону комірок, то цю адресу можна набрати я к з клавіатури, так і за допомогою миші (виділити цей діапазон, затиснувши ліву кнопку).

За допомогою миші виділяємо діапазон комірок Н2:К5. Натискаємо клавішу <F2>, потім одночасно натискаємо клавіші <Ctrl>+<Shift>+<Enter>.

Увага!! Послідовність дій, виділених курсивом, завжди використовується при роботі з масивами (матрицями та векторами: обертання, множення, транспонування тощо).

Результат обертання матриці зображено на рис. 0.5.

Увага!! У комірці К3 записаний вираз «2,5Е-17». Такий формат запису застосовується для чисел, які дуже близькі до нуля. Так, число, записане у комірці К3: .

6. Функція «=МОПРЕД(масив)» - повертає визначник матриці.

Приклад. У комірці А3 обчислимо визначник матриці з попереднього прикладу (масив С2:F5). Набираємо команду «=МОПРЕД(С2:F5)» та натискаємо <Enter>. Визначник матриці дорівнює 66.

7. Функція «=МУМНОЖ(масив1;масив2)» - повертає добуток матриць.

Приклад. У масиві С9:Е12 запишемо елементи матриці В (рис. 0.5). Виконаємо множення матиці А (з попередніх прикладів, масив С2:F5) на матрицю В. Перш ніж множити матриці, потрібно перевірити, чи можливе взагалі таке множення. Нагадаємо, що множити дві матриці можна лише тоді, коли число стовпчиків першого множника дорівнює числу рядків другого множника. У нашому прикладі така умова виконана: матриця А має розміри , матриця В має розміри . Отже, добуток матиме розміри . Обираємо діапазон комірок (масив) G9:I12. У лівому верхньому кутку цього масиву (комірка G9) набираємо команду «=МУМНОЖ(C2:F5;C9:E12)» та натискаємо <Enter>. Потім виділяємо масив G9:I12. Натискаємо клавішу <F2>, потім одночасно натискаємо клавіші <Ctrl>+<Shift>+<Enter>.

8. Функція «=ТРАНСП(масив)» - повертає транспоновану матрицю.

Приклад. Транспонуємо матрицю з попереднього прикладу. Якщо матриця має розміри , то транспонована матриця матиме розміри . Спочатку треба визначитися, у якому діапазоні комірок буде розташовуватися ця матриця. Обираємо, наприклад, діапазон комірок К9:N11. У лівому верхньому кутку цього діапазону (у комірці К9) набираємо команду «=ТРАНСП(С9:Е12)» та натискаємо <Enter>.

Виділяємо масив К9:N11. Натискаємо клавішу <F2>, потім одночасно натискаємо клавіші <Ctrl>+<Shift>+<Enter>.

Рисунок 0.5 – Дії з матрицями

Функції категорії «Статистические»

Фіксація координат комірок

Можливості АВТОЗАПОВНЕННЯ значно збільшуються, якщо використовувати фіксацію координат комірок.

Приклад. Нехай потрібно помножити усі числа масиву С9:Е12 на число, записане у комірці А15. Фактично треба виконати множення матриці на число. Результатом буде матриця С таких же розмірів , як і матриця В. Розраховуємо елементи цієї матриці у масиві С15:Е18. Для цього розташовуємо курсор у комірці С15 та набираємо у цій комірці команду «=C9*$A$15». Решту елементів масиву знаходимо АВТОЗАПОВНЕННЯМ.

Справа в тому, що при використанні АВТОЗАПОВНЕННЯ у результаті переміщення вздовж рядка у використовуваній формулі автоматично змінюється координата стовпчика. Щоб цього не сталося (у разі необхідності), за допомогою символу «$» відповідна координата (стовпчик) фіксується і залишається незмінною в усьому діапазоні застосування формули. Аналогічно залишається незмінною інша координата (рядок) при переміщенні вздовж стовпчика.

У разі потреби можна фіксувати не дві, а лише одну координату.

Приклад. Нехай потрібно помножити числа масиву С2:F5 (матриця А) на числа, записані у комірках G14:J14 наступним чином: числа С2:С5 помножити на число G14; числа D2:D5 помножити на число Н14; числа Е2:Е5 помножити на число I14; числа F2:F5 помножити на число J14. Тобто, кожен стовпчик матриці А множиться на «своє число». Зрозуміло, що при використанні АВТОЗАПОВНЕННЯ, при переміщенні по рядках, номер стовпчика повинен змінюватись у обох множників. Отже, у формулі потрібно зафіксувати лише номер стовпчика.

Результати множення (матриця D) розмістимо у масиві G16:J19. Таким чином, у комірці G16 набираємо команду «=C2*G$14». Решту обчислюємо АВТОЗАПОВНЕННЯМ.

Рисунок 0.6 – Приклади фіксації комірок

9. Функція «=СУММ(число1;число2;…)» - повертає суму чисел.

10. Функція «=СРЗНАЧ(число1;число2;…)» - повертає середнє арифметичне чисел (кількість чисел не більше 30). Обчислення виконуються за формулою ( кількість чисел):

.

11. Функція «=ДИСП(число1;число2;…)» - повертає незміщену дисперсію вибірки (обсяг вибірки не перевищує 30 чисел). Обчислення виконуються за формулою:

.

12. Функція «=ДИСПР(число1;число2;…)» - повертає дисперсію генеральної сукупності (обсяг сукупності не перевищує 30 чисел). Обчислення виконуються за формулою:

.

13. Функція «=КОРРЕЛ(масив1;масив2)» - повертає коефіцієнт лінійної кореляції між двома множинами даних.

14. Функція «=СТАНДОТКЛОН(число1;число2;…)» - повертає незміщене стандартне відхилення вибірки (обсяг вибірки не перевищує 30 чисел). Обчислення виконуються за формулою:

.

15. Функція «=СТАНДОТКЛОНП(число1;число2;…)» - повертає стандартне відхилення генеральної сукупності (обсяг сукупності не перевищує 30 чисел). Обчислення виконуються за формулою:

.

Приклад. Маємо два масиви чисел у комірках D23:D32 та E23:E32 (рис. 0.7).

У рядку 33 стовпчиків D та Е обчислимо суми чисел відповідних масивів. Для цього в комірці D33 виконуємо команду «=СУММ(D23:D32)», обчислення у комірці Е33 виконуємо АВТОЗАПОВНЕННЯМ.

У рядку 34 стовпчиків D та Е обчислимо середні арифметичні значення відповідних масивів чисел. Для цього в комірці D34 виконуємо команду «=СРЗНАЧ(D23:D32)», обчислення у комірці Е34 виконуємо АВТОЗАПОВНЕННЯМ.

У рядку 35 стовпчиків D та Е обчислимо незміщені дисперсії вибірки. Для цього в комірці D35 виконуємо команду «=ДИСП(D23:D32)»; обчислення у комірці Е35 виконуємо АВТОЗАПОВНЕННЯМ.

У рядку 36 стовпчиків D та Е обчислимо дисперсії генеральної сукупності. Для цього в комірці D36 виконуємо команду «=ДИСПР(D23:D32)»; обчислення у комірці Е36 виконуємо АВТОЗАПОВНЕННЯМ.

Аналогічно обчислюємо стандартні відхилення у 37 та 38 рядках.

Обчислення У комірці D39 обчислюємо коефіцієнт лінійної кореляції між множинами чисел комірках D23:D32 та E23:E32 за допомогою команди «=КОРРЕЛ(D23:D32;E23:E32)».

Рисунок 0.7 – Статистичні розрахунки

Висновки:

У ході виконання лабораторної роботи досліджені можливості Майстра функцій MS EXCEL, які можуть бути використані при розв’язуванні економетричних задач.