7.3. Оцінювання параметрів авторегресійних моделей

Три авторегресійних моделі — Койка (7.2), адаптивних сподівань (7.3) і часткового коригування (7.4) — можна подати в загальній формі:

(7.5)

Наявність лагових залежних змінних у динамічних моделях ство­рює певні проблеми при оцінюванні параметрів: серед пояснюючих змінних є стохастичні (залежні лагові змінні), а також існує пробле­ма серійної кореляції залишків моделі та лагових змінних. Залежно від гіпотез щодо залишків таких моделей використовують відповідні методи оцінювання.

Гіпотеза 1. Залишки є нормально розподіленими випадковими ве­личинами з нульовим математичним сподіванням та сталою диспер­сією.

Гіпотеза 2. Залишки описуються авторегресійною схемою першо­го порядку:

.

Гіпотеза 3. Залишки автокорельоваиі та описуються авторегресій­ною схемою першого порядку:

,

крім того, .

Перша гіпотеза виконується лише для моделі часткового коригуван­ня (7.4); саме для неї можливе застосування звичайного МНК. Однак залежність залишків від лагової змінної у цій моделі призводить до зміщення оцінок параметрів. Та хоча оцінки параметрів будуть зави­щеними, вони матимуть найменшу середньоквадратичну похибку. І після визначення величини зміщення МНК-оцінки будуть найприйнятнішими.

Якщо залишки моделі визначаються через автокорельоваиі випад­кові величини, то МНК-оцінки параметрів моделі також матимуть зміщення, до того ж зміщення матиме також критерій Дарбіна—Уотсона. Тому для перевірки автокореляції залишків застосовують уза­гальнений критерій Дарбіна—Уотсона. Оцінювання параметрів та­ких моделей виконують узагальненим методом найменших квадратів (методом Ейткена), в операторі оцінювання якого

коригуючи матриця має вигляд:

.

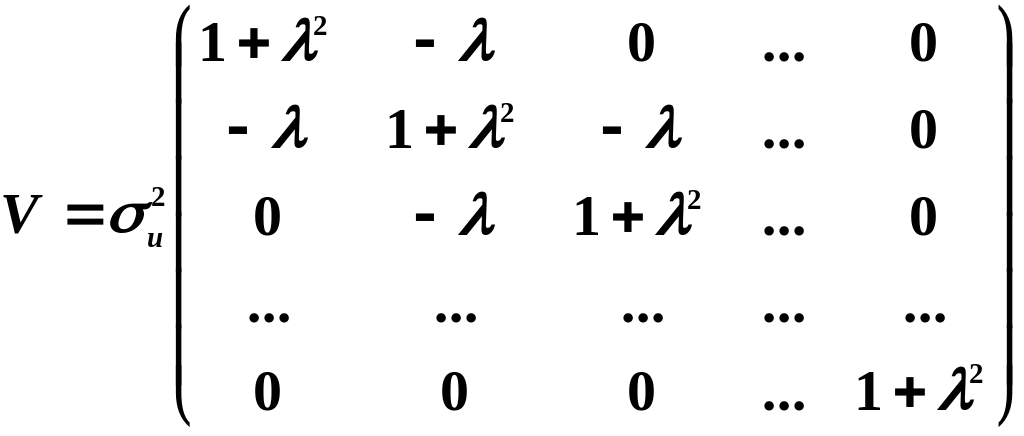Якщо лагову модель можна подати у вигляді:

,

то до перетворених у такий спосіб даних залежної змінної застосову­ють звичайний МНК. Причому параметр вибирають з інтервалу так, щоб мінімізувати суму квадратів залишків .

Якщо відносно залишків моделі приймається третя гіпотеза, то па­раметри оцінюють за допомогою таких методів:

1. класичного МНК після попереднього перетворення вхідних даних;

2. методу Ейткена (узагальненого МНК);

3. ітераційного методу;

4. методу інструментальних змінних;

5. алгоритму Уолліса.

Контрольні запитання

1. Що в економіці називається лагом?

2. Що є причиною лага?

3. Які регресійні моделі називають авторегресійними та дистрибутивно-лаговими?

4. Якою є природа авторегресійних моделей?

5. Які проблеми виникають при оцінюванні параметрів дистрибутивно-лагових і авторегресійних моделей?

6. Які гіпотези висуваються щодо залишків лагових моделей?

7. Якими методами оцінюються параметри дистрибутивно-лагових і авторегресійних моделей?

Тема 8. Системи одночасних рівнянь

8.1. Поняття про системи одночасних рівнянь

Багато економічних взаємозв'язків допускають моделювання од­ним рівнянням. Однак деякі економічні процеси моделюються не од­ним, а кількома рівняннями. Співвідношення між економічними по­казниками можуть мати стохастичний і детермінований характер. Стохастичні зв'язки між змінними описуються регресійними рівнян­нями, а детерміновані визначаються тотожностями й не містять не­відомих параметрів.

У системах рівнянь через наявність прямих і зворотних зв'язків залежна змінна одного рівняння може бути незалежною змінною в інших рівняннях. Змінні, що стоять у лівій частині рівнянь, назива­ються ендогенними, причому їх кількість не перевищує загальної кількості всіх рівнянь. Інші змінні, що входять до моделі, називаються екзогенними.

Наприклад, повна кейнсіанська модель доходу складається з двох співвідношень:

(8.1),

(8.2),

де — витрати на споживання; — дохід; — невідомі па­раметри; — залишки моделі; — неспоживчі витрати (інвес­тиції).

Перше співвідношення — це регресійна функція споживання, а друге - тотожність доходу. Величина доходу для першого рівнян­ня є незалежною змінною, для другого — залежною, а величина — навпаки: у першому рівнянні вона є залежною змінною, у другому — незалежною. Для системи загалом змінні і є ендогенними, а змін­на — екзогенною.

Означення 8.1. Для систем одночасних рівнянь усі змінні, що можуть бути визначені із системи рівнянь, називаються ендогенни­ми, причому їх кількість не перевищує загальної кількості рівнянь.

Означення 8.2. Для систем одночасних рівнянь усі змінні, які за­даються за межами моделі або є заздалегідь відомими, називаються відповідно екзогенними або предетермінованими.

У розглянутій кейнсіанській моделі доходу величини і є ен­догенними змінними, що визначаються всередині моделі. Змінна задається (визначається) поза моделлю, отже, вона є екзогенною.

Із першого співвідношення цієї моделі видно, що змінна за­лежить від доходу і від залишків , а з другого співвідношення очевидна залежність доходу від споживчих і неспоживчих витрат . Неважко помітити, що обидві змінні і можуть бути виражені через і залишки .