Контрольні запитання

1. Що означає автокореляція залишків?

2. Які причини виникнення автокореляції?

3. Чим відрізняється УМНК при автокореляції?

4. До яких наслідків призводить автокореляція залишків?

5. Як впливає автокореляція на оцінку параметрів моделі?

6. Наведіть тести наявності автокореляції залишків.

7. Дайте стислу характеристику алгоритму методу Дарбіна – Уотсона.

8. Зобразіть графічно зони автокореляційного зв'язку за критерієм Дарбіна– Уотсона.

9. Охарактеризуйте алгоритм критерію фон Неймана.

10. На основі яких методів можна оцінити параметри моделі з автокорельованими залишками?

11. У яких випадках для оцінки параметрів економетричної мо­делі з автокорельованими залишками доцільно застосовувати ітераційні методи Кочрена – Оркатта або Дарбіна?

12. Що таке нециклічний коефіцієнт автокореляції?

13. Що таке циклічний коефіцієнт автокореляції?

Тема 7. Моделі розподіленого лага

7.1. Поняття лага та лагових моделей в економіці

Для багатьох економічних процесів типово, що ефект від впливу деякого фактора па показник, який характеризує процес, виявляєть­ся не одразу, а поступово, через деякий час або протягом деякого часу. Таке явище називається запізнюванням (затримкою), а проміжок часу, у який спостерігається це запізнювання, — часовим лагом, або просто лагом.

Наприклад, функція споживання після різкої зміни доходу також змінюється, але не пропорційно до доходу. Зокрема, зі збільшенням доходу витрати значно зростають (задовольняються нагальні потре­би), а потім можуть зменшуватися за рахунок збільшення інвестицій (плануються великі витрати і зростають нагромадження, а споживан­ня зменшується). Вкладання коштів у наукові дослідження не одра­зу впливає па зростання продуктивності праці — має пройти певний час від виникнення наукової ідеї до її впровадження у виробництво. Капітальне будівництво також не дає миттєвих прибутків і т. ін.

Означення 7.1. Моделі, у яких досліджуваний показник у момент часу визначається не лише поточними, а й попередніми значення­ми незалежних змінних, називаються дистрибутивно-лаговими:

.

Означення 7.2. Моделі, у яких досліджуваний показник у момент часу визначається своїми попередніми значеннями, називаються авторегресійними або динамічними моделями. Наприклад,

Змінні i у період називаються лаговими змінни­ми, а величина — періодом зсуву (лагом).

Якщо в економетричній моделі незалежні змінні використовують за кілька попередніх періодів, то такі моделі називають моделями з кінцевим лагом (скінченими моделями). Якщо вплив незалежної змінної не обмежується певним періодом, розглядають нескінченні лагові моделі.

Звичайно, нескінченна лагова модель більш загальна, однак прак­тичне застосування такої моделі досить проблематичне через велику кількість факторів, складність внутрішньої структури та обмеженість часових рядів — інформаційної бази моделей.

Коефіцієнти називаються коефіцієнтами лага, а послідовність — структурою лага.

Коефіцієнт при незалежній змінній , що відбиває її вплив на залежну змінну в поточний період, називається короткостроковим, або впливовим, мультиплікатором. Часткові суми коефіцієнтів , що відображають зміну в другий, третій і наступні періоди, називаються проміжними інтервалами. Загаль­на сума лагових коефіцієнтів для всієї моделі називається довгостроковим, або загальним, дистрибутивно-лаговим мультиплікатором.

Остання сума для скінчених моделей, очевидно, є скінченим числом. Для нескінченної моделі лагові коефіцієнти за певних умов також можуть утворити скінчену суму. Якщо кожен із коефіцієнтів розділити на їх суму, отримаємо відповідно нормовані коефіцієнти лага та нормовану структуру лага.

Усі нормовані коефіцієнти менші від одиниці, а їх сума дорівнює одиниці.

Дистрибутивно-лагові моделі, які ще називають моделями роз­поділеного лага, задовільно описують економічні процеси лише в стабільних (незмінних) умовах. Необхідність враховувати ще й по­точні умови функціонування вимагає застосування узагальнених мо­делей.

Означення 7.3. Якщо економетрична модель містить не лише лагові змінні, а й змінні, що безпосередньо виливають на дослід­жуваний показник (тобто містить й поточні умови функціонуван­ня), то така модель називається узагальненою моделлю розподіле­ного лага:

.

Оцінювання параметрів таких рівнянь ускладнюється обмеження­ми, що накладаються на коефіцієнти при лагових змінних.

Перш ніж будувати економетричиу модель з лаговими змінними, необхідно обґрунтувати величину лага. Для цього застосовують взає­мну кореляційну функцію — послідовність коефіцієнтів кореляції, які визначають ступінь зв'язку кожного елемента вектора залежної змінної з елементом вектора незалежної змінної, зсунутими один відносно одного на часовий лаг :

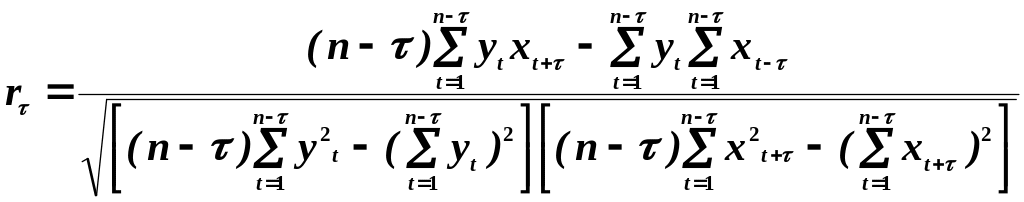(7.1).

Серед отриманих коефіцієнтів кореляції вибирають найбільший за модулем, а відповідне значення часового зсуву вважають лагом. Якщо таких коефіцієнтів кілька, застосовують модель розподіленого лага.

Приклад. На основі взаємопов'язаних часових рядів, які ха­рактеризують чисту продукцію та капітальні вкладення регіону за 20 років, побудувати взаємну кореляційну функцію, вико­риставши дані табл. 7.1.

У результаті розрахунків, виконаних за формулою (7.1) для різних значень , отримано значення коефіцієнтів кореляції, що на­ведені в табл. 7.2.

З табл. 7.2 видно, що найбільше значення коефіцієнта кореляції . Він відповідає значенню . Це означає, що найбільшого виливу капітальних вкладень на обсяг чистої про­дукції слід очікувати впродовж третього року.

Таблиця 7.1

Дані до задачі

Рік	Капітальні вкладення, млн. грн.	Чиста продукція, млн. грн.	Рік	Капітальні вкладення, млн. грн.	Чиста продукція, млн. грн.
1	3857	24334	11	17006	72165
2	4686	28678	12	17352	78743
3	5515	33021	13	17838	80381
4	5209	32432	14	18878	82204
5	7522	40325	15	19090	77833
6	10390	49334	16	20016	81413
7	13678	54717	17	17736	77484
8	15976	53818	18	11951	75443
9	13880	55968	19	11469	85038
10	13949	61517	20	9068	75809

Таблиця 7.2

Кореляційна функція

	0	1	2	3	4	5	6	7	8	9	10
	0,827	0,866	0,899	0,924	0,920	0,923	0,857	0,747	0,633	0,389	0,050

Динамічна модель розподіленого лага в такому разі має вигляд

,

де чиста продукція в період ; вагові коефіцієнти лагових змінних; — капітальні вкладення в період .