6.3. Параметризація моделі з автокорельованими залишками

Параметри моделі з автокорельованими залишка­ми можна оцінити на основі чотирьох методів:

1. Ейткена (УМНК);

2. Перетворення вихідної інформації;

3. Кочрена – Оркатта;

4. Дарбіна.

Перші два методи доцільно застосовувати тоді, коли залишки описуються авторегресійною моделлю першого порядку.

Ітераційні методи Кочрена – Оркатта і Дарбіна можна застосо­вувати для оцінки параметрів економетричної моделі також тоді, коли залишки описуються авторегресійною моделлю вищого порядку.

6.4. Приклад

На основі двох взаємопов'язаних часових рядів про роздрібний то­варообіг і доходи населення побудувати модель, що характеризує за­лежність роздрібного товарообігу від доходу, перевірити автокореляцію залишків.

Вихідні дані наведено в таблиці 6.1.

Таблиця 6.1

Дані до задачі (млн.. грн.)

Рік	Товарообіг	Дохід
1	25,5	27,6
2	26,4	27,4
3	27,9	28,7
4	28,1	29,5
5	28,8	30,9
6	29,3	31,4
7	29,8	31,8
8	30,7	32,2
9	31,5	33,6
10	32,4	34,7

Розв'язання

1. Ідентифікуємо змінні моделі: залежна змінна роздрібний товарообіг, незалежна змінна дохід населення.

2. Специфікуємо модель у лінійній формі: .

3. Визначимо , на основі МНК, припустивши, що залишки некорельовані:

Отже, модель має вигляд:

.

4. Знайдемо оцінені значення товарообігу на основі отриманої моделі та визначимо залишки .

Таблиця 6.2

Допоміжні розрахунки

Рік
1	25,5	27,6	26,27880	-0,77880	0,60653
2	26,4	27,4	26,10514	0,29486	0,08694	-0,77880	1,15275	-0,22964
3	27,9	28,7	27,23393	0,66607	0,44365	0,29486	0,13779	0,19640
4	28,1	29,5	27,92857	0,17143	0,02939	0,66607	0,24467	0,11418
5	28,8	30,9	29,14420	-0,34420	0,11847	0,17143	0,26587	-0,05900
6	29,3	31,4	29,57835	-0,27835	0,07748	-0,34420	0,00434	0,09581
7	29,8	31,8	29,92567	-0,12567	0,01579	-0,27835	0,02331	0,03498
8	30,7	32,2	30,27299	0,42701	0,18234	-0,12567	0,30545	-0,05366
9	31,5	33,6	31,48861	0,01139	0,00013	0,42701	0,17274	0,00486
10	32,4	34,7	32,44375	-0,04375	0,00191	0,01139	0,00304	-0,00050
Сума	290,4	307,8	290,4	0,00000	1,56263	0,04375	2,30996	0,10343

5. Обчислимо оцінку -статистики Дарбіна­­ –Уотсона:

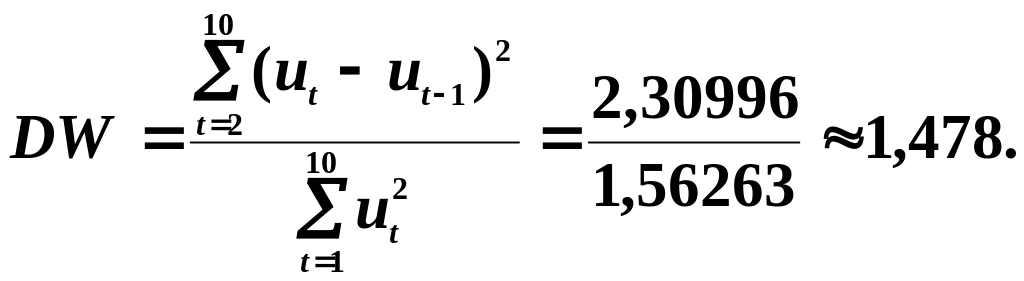
Задамо і при та знайдемо за таблицею значень -статистики Дарбіна­–Уотсона критичні значення критерію:

– нижня межа – верхня межа

Оскільки то з похибкою щонайбільше у 5% ви­падків можна стверджувати, що автокореляція залишків відсутня.

6. Перевіримо автокореляцію за­лишків моделі на основі критерію фон Неймана.

Обчислюємо фактичне значення критерію фон Неймана:

Звідси .

Таб­личне значення критерію фон Неймана при рівні значущості і заданій кількості спостережень : .

Так як , то автокореляція залишків відсутня.