6.2. Тестування наявності автокореляції

Тестування наявності автокореляції, як правило, здійснюється за -тестом Дарбіна – Уотсона, хоча існують й інші не менш відомі тес­ти: критерій фон Неймана, нециклічний коефіцієнт автокореляції, циклічний коефіцієнт автокореляції.

6.2.1. Критерій Дарбіна – Уотсона

(складається з кількох етапів і включає зони невизначеності)

Крок 1. Розраховується значення -статистики за формулою

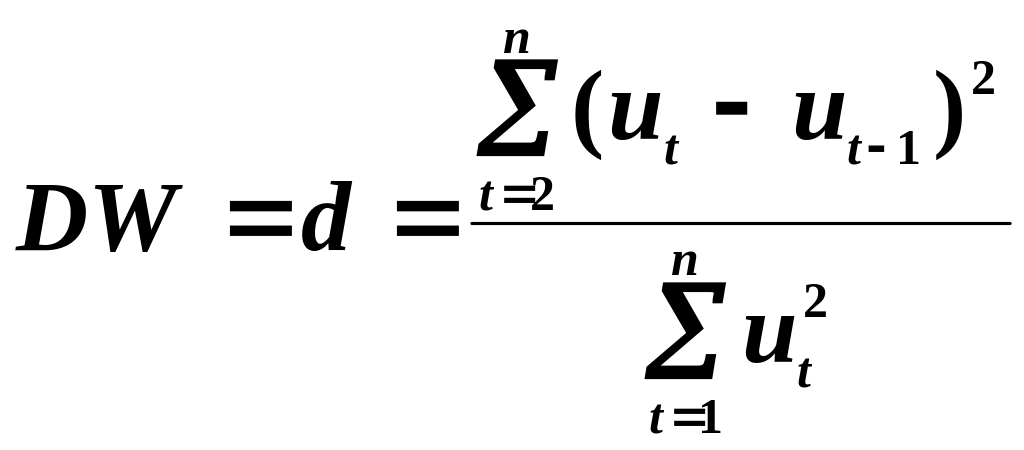. (6.4)

Зауваження. Доведено, що значення -статистики Дарбіна – Уот­сона перебуває в межах .

Крок 2. Задаємо рівень значущості . За таблицею значення -статистики Дарбіна –Уотсона при заданому рівні значущості , кількості факторів і кількості спостережень знаходимо два значення і :

Якщо то наявна додатна автокореляція.

Якщо або , ми не може­мо зробити висновки ані про наявність, ані про відсутність ав­токореляції ( потрапляє в зону невизначеності).

Якщо маємо від'ємну автокореляцію.

Якщо то автокореляція відсутня.

Графічне зображення розподілу ілюструє рис. 6.1.

Рисунок 6.1 – Зони авто кореляційного зв’язку за критерієм Дарбіна –Уотсона

6.2.2. Критерій фон Неймана

За цим критерієм розраховується

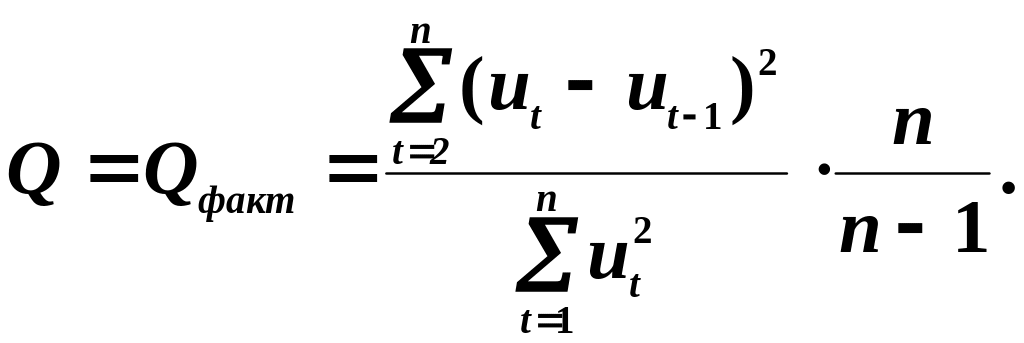
Звідси . Отже, при

Фактичне значення критерію фон Неймана порівнюється з таб­личним при вибраному рівні значущості і заданій кількості спостережень : .

Якщо , то автокореляція існує, у іншому випадку автокореляція відсутня.

6.2.3. Коефіцієнти автокореляції та їх застосування

Окрім статистик Дарбіна – Уотсона та Неймана, для перевірки ав­токореляції застосовують також нециклічний коефіцієнт автокореляції , який відображає ступінь взаємозв’язку рядів і обчислюється формулою

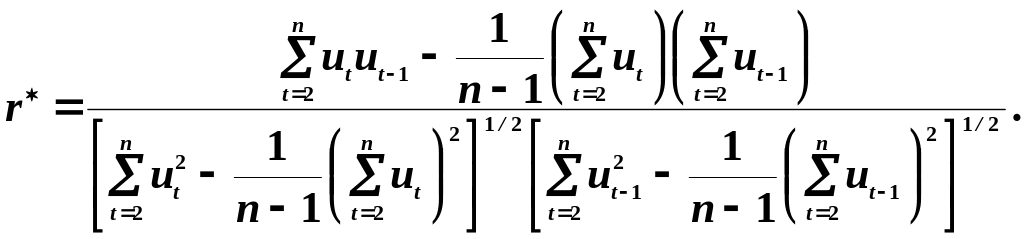
Коефіцієнт може набувати значень в інтервалі . Його від'ємні значення свідчать про від'ємну автокореляцію залишків, а до­датні – про додатну автокореляцію. Значення, що лежать в деякій кри­тичній області поблизу нуля, підтверджують нульову гіпотезу про відсутність автокореляції в залишках. Оскільки імовірнісний розпо­діл встановити важко, то на практиці замість обчислюють цик­лічний коефіцієнт автокореляції . Загалом, якщо часовий ряд має циклічний характер, тобто припускається, що після значення загаль­ний характер зміни членів ряду повторюється, то автокореляцію виз­начають за допомогою коефіцієнта , запровадженого Андерсоном.

При цьому автокореляція визначається між послідовностями, зсу­нутими на період :

і

і

Якщо період , то маємо коефіцієнт циклічної автокореляції першого порядку, який відбиває інтенсивність взаємозв'язку між по­слідовностями

і

Для досить довгих рядів вплив циклічних членів стає незначним, тому імовірнісний розподіл коефіцієнта наближається до імовір­нісного розподілу коефіцієнта циклічної автокореляції , який об­числюється за формулою

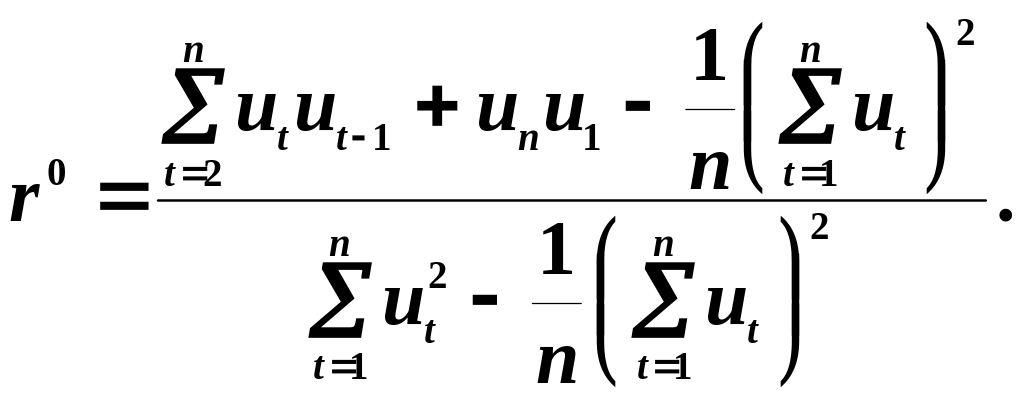
Якщо останній член ряду дорівнює першому, тобто , то нециклічний коефіцієнт автокореляції дорівнює циклічному. Очевид­но, якщо залишки не містять тренда, то припущення про рівність недалеке від дійсності й циклічний коефіцієнт автокореляції близький до нециклічного. Крім того, припускаючи, що середня за­лишків дорівнює нулю, тобто , а отже, ,

отримуємо приблизну формулу для обчислення циклічного коефіці­єнта автокореляції:

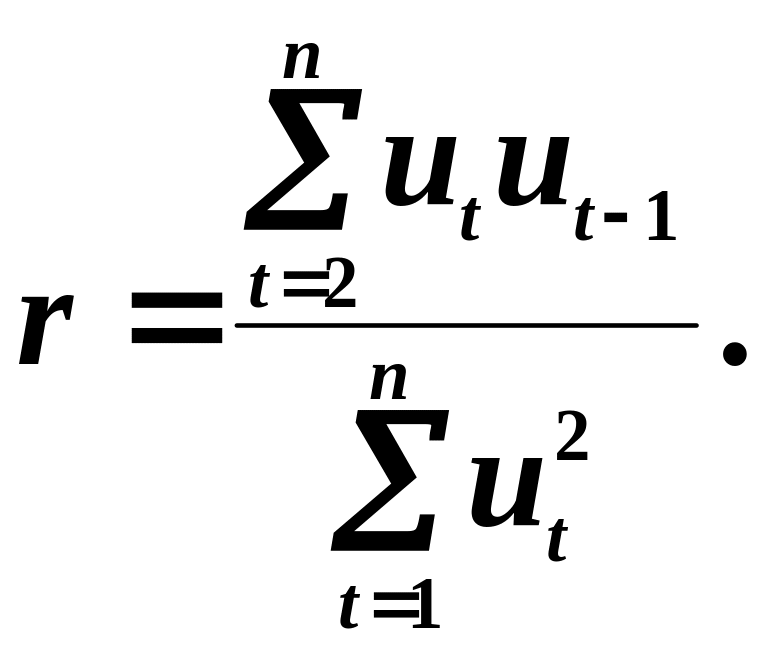
При цьому Значення використовується при оцінюванні параметрів моделі.