4.4. Приклад дослідження наявності мультиколінеарності на основі алгоритму Фаррара–Глобера

Розглянемо дослідження впливу на економічний показник – ре­альне споживання країни (у млрд.. грн.) трьох факторів: – купівлі та оплати товарів і послуг (у млрд.. грн.), – усіх заощаджень від загаль­ного грошового доходу (у % від загальної суми доходу), – рівня став­ки ПДВ (у %). Необхідно перевірити фактори на мультиколінеарність.

Таблиця 4.1

Дані до задачі

№ п/п
1	25,74	4,69	11,97	29,23
2	25,34	5,64	13,43	29,35
3	31,26	6,26	12,92	33,40
4	33,50	6,99	14,74	30,97
5	32,30	6,36	14,64	32,92
6	38,90	7,60	17,10	37,27
7	41,58	7,12	15,63	30,97

Таблиця 4.1 (продовження)

8	48,02	6,81	15,35	33,58
9	43,30	8,67	15,85	35,62
10	51,78	7,83	18,05	34,99
11	52,14	7,84	17,24	39,34
12	54,94	8,85	20,52	41,50
13	59,18	9,61	19,18	45,58
14	62,22	10,67	19,03	41,08
15	63,62	11,04	21,45	40,54
16	65,01	11,85	22,25	42,75
17	67,78	12,94	24,75	43,89
18	71,45	14,24	25,03	41,95
19	75,24	15,67	27,87	44,06
20	77,38	16,33	30,48	46,77

Розв'язання

1-й крок:

нормалізуємо змінні економетричної моделі за формулою:

де кількість спостережень; кількість незалежних змінних; – середня арифметична незалежної змінної ; – середнє квадратичне відхилення незалежної змінної .

Обчислюємо середні арифметичні значення:

Обчислюємо середні квадратичні відхилення:

Будуємо матрицю нормалізованих змінних .

2-й крок:

Будуємо кореляційну матрицю (формула 4.2):

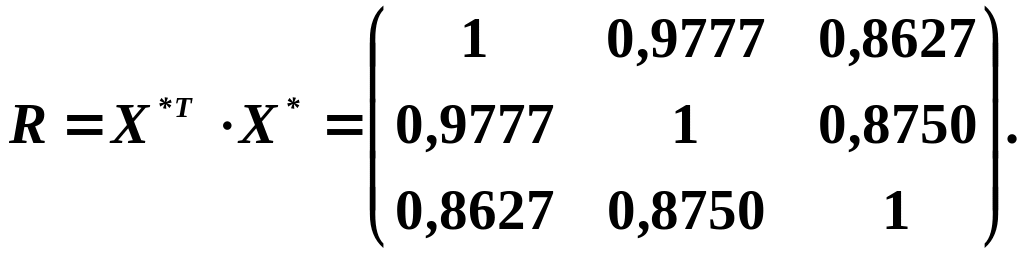
3-й крок:

Обчислюємо визначник кореляційної матриці R:

.

Обчислимо експериментальне значення критерію (формула 4.3):

.

Порівняємо значення з табличним при ступе­нях свободи та рівні значущості : .

Так як , то в масиві незалежних змінних існує мультиколінеарність у сукупності.

4-й крок:

визначимо матрицю похибок (формула 4.4):

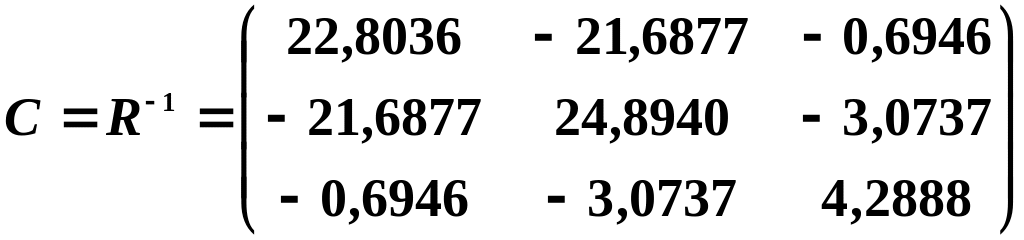
5-й крок:

Розрахуємо експериментальні значення критеріїв (формула 4.5):

.

Розраховані значення критеріїв порівняємо з табличним при рівні значущості та ступенях свободи і :

.

Оскільки кожне експериментальне значення більше від табличного: робимо висновок, що кожна незалежна змінна мультиколінеарна з іншими.

Визначимо коефіцієнти детермінації для кожної змінної (формула 4.6):

6-й крок:

знайдемо часткові коефіцієнти кореляції (формула 4.7), які характеризують щільність зв'язку між двома змінними за умови, що інші змінні не впливають на цей зв'язок (існування парної мультиколінеарності):

Якщо порівняти абсолютні значення часткових і парних ко­ефіцієнтів, то можна побачити, що перші значно менші, ніж останні. Тому на основі знання часткових коефіцієнтів кореляції висновок про мультиколінеарність робити неможливо. Для цього необхідно ще ви­конати 7-й крок.

7-й крок:

Розрахуємо експериментальні значення критеріїв (формула 4.8):

Розраховані значення критеріїв порівняємо з табличним при рівні значущості та ступенях свободи:

Оскільки , , то між першою та дру­гою незалежними змінними існує мультиколінеарність.

Висновок: у масиві незалежних змінних існує мультиколінеарність. Доцільно виключити з масиву незалежних змінних або змінну або змінну та будувати двохфакторну лінійну модель.