3.6. Етапи дослідження загальної лінійної моделі множинної регресії

Розглядається багатофакторна лінійна регресійна модель

що описує залежність між результативною змінною та деякими; впливовими факторами . Інформація про значення міститься у відповідних статистичних даних – спостереженнях (вимірюваннях) кожного показника.

Для дослідження зазначеної моделі слід виконати такі кроки.

1. За даними спостережень оцінити параметри .

2. Для перевірки адекватності отриманої моделі обчислити:

а) залишки моделі – розбіжності між спостереженими та розра­хунковими значеннями залежної змінної , ;

б) відносну похибку залишків та її середнє значення;

в) залишкову дисперсію;

г) коефіцієнт детермінації;

д) вибірковий коефіцієнт множинної кореляції.

3. Перевірити статистичну значущість отриманих результатів:

а) перевірити адекватність моделі загалом: за допомогою критерію Фішера перевірити гіпотезу

проти альтернативної Н_А: існує хоча б один коефіцієнт ;

б) перевірити значущість коефіцієнта множинної кореляції, тобто розглянути гіпотезу ;

в) перевірити істотність кожного коефіцієнта регресії: за допо­могою t-критерію Стьюдента перевірити гіпотезу

для всіх

проти відповідних альтернативних гіпотез

для всіх .

4. Обчислити та інтерпретувати коефіцієнти еластичності.

5. Побудувати довірчі інтервали для параметрів регресії.

6. Обчислити прогнозні значення за значеннями , що перебувають за межами базового періоду, і знайти межі довірчих інтервалів індивідуальних прогнозованих значень і межі довірчих інтервалів середнього прогнозу.

Приклад параметризації та дослідження багатофакторної регресійної моделі

Розглянемо задачу дослідження впливу на економічний показник трьох факторів , а саме досліджуватимемо залежність при­бутку підприємства від інвестицій , витрат на рекламу та витрат на заробітну плату .

Таблиця 3.1

Вихідні дані, млн.. грн.

Номер спостереження,	Прибуток підприємства,	Обсяг інвестицій,	Витрати на рекламу,	Витрати на зарплату,
1	15,70	17,37	5,28	1,42
2	17,34	18,24	6,47	1,58
3	21,57	22,47	6,98	1,98
4	33,50	18,47	7,05	2,04
5	32,30	16,82	7,94	2,38
6	37,90	17,60	8,12	3,48
7	40,78	17,12	8,69	3,07

Таблиця 3.1 (продовження)

8	48,02	19,81	9,31	3,84
9	43,30	18,67	10,45	4,28
10	49,57	20,83	10,47	4,67
11	52,14	22,84	13,48	5,98
12	55,17	28,85	15,78	6,51
13	59,18	29,61	17,65	7,82
14	62,22	35,67	18,47	8,58
15	77,58	47,87	19,64	9,47

Розв’язання:

Припустимо, що між економічним показником і факторами існує лінійний зв'язок.

Запишемо рівняння регресії у вигляді

(3.3).

1. Знайдемо за МНК оцінки параметрів моделі (3.3). Для цього складемо вектор-стовпець Y і матрицю X :

Обчислимо оцінки регресійних коефіцієнтів за формулою (3.2):

.

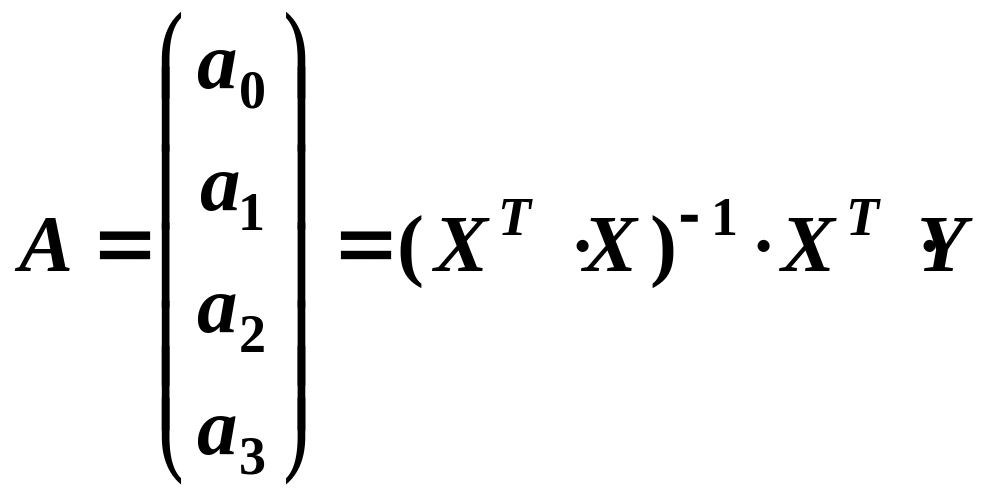Знаходимо матрицю моментів:

Знаходимо матрицю помилок:

Обчислюємо добуток та знаходимо вектор оцінок параметрів моделі:

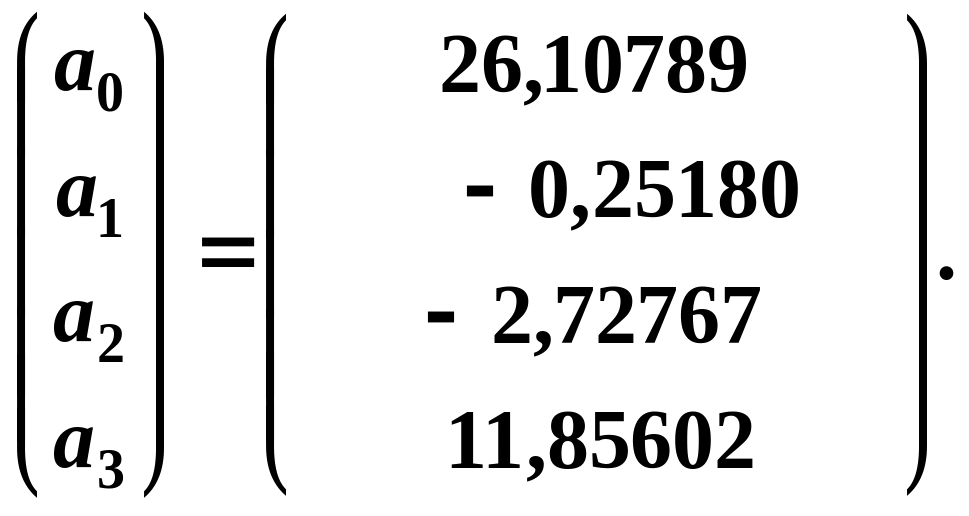
Отже, трьохфакторна лінійна економетрична модель має вигляд:

(3.4).

2. Для перевірки адекватності отриманої моделі обчислимо:

а) залишки моделі – розбіжності між спостереженими та розрахованими за формулою (3.4) при заданих спостереженнях значеннями залежної змінної:

, ;

Зауваження. Обчислення значень можна виконати у матричному вигляді за формулою .

Маємо:

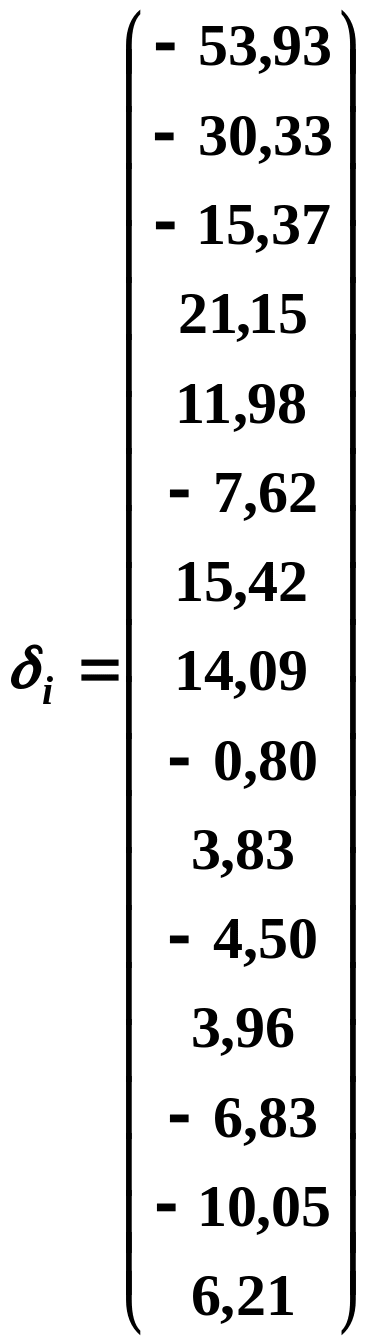
б) відносну похибку розрахункових значень регресії:

середнє значення відносної похибки:

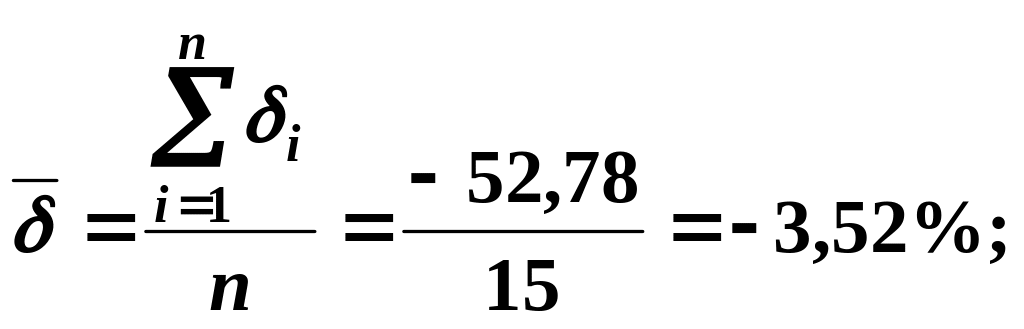
в) середньоквадратичну похибку дисперсії залишків:

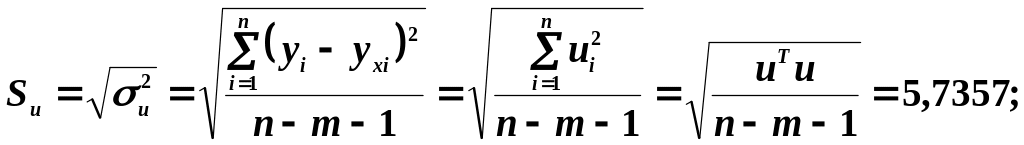
(чим менша стандартна похибка S, тим краще функція регресії відповідає дослідним даним);

г) коефіцієнт детермінації, тобто перевіримо загальний вплив не­залежних змінних на залежну змінну:

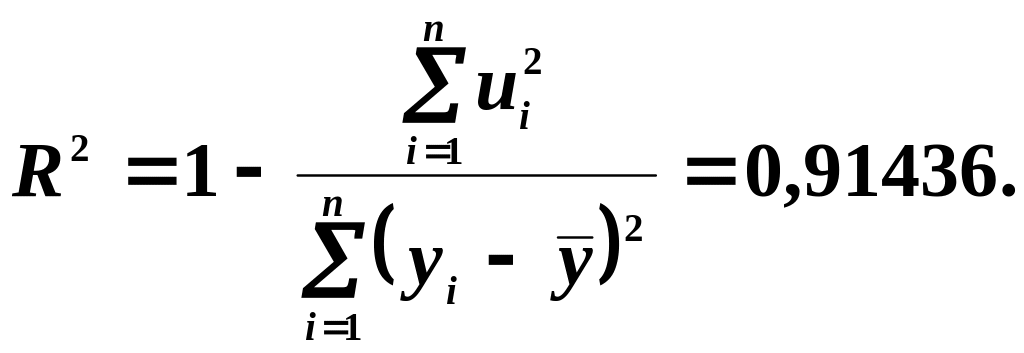
Висновок: оскільки коефіцієнт детермінації наближається до оди­ниці, варіація залежної змінної Y значною мірою визначається варіа­цією незалежних змінних;

д) вибірковий коефіцієнт множинної кореляції:

Коефіцієнт кореляції досить великий, тому існує тісний лінійний зв'язок усіх незалежних факторів із залежною змінною .

3. Перевіримо статистичну значущість отриманих результатів:

а) обчислимо статистику за формулою (спрощений варіант для перевірки нульової гіпотези: ):

Знайдемо табличне значення статистики :

.

Порівняємо експериментальне (фактичне) значення статистики з табличним.

Оскільки , то нульова гіпотеза відхиляється, тоб­то коефіцієнти регресії є значущими, побудована лінійна трьохфакторна модель є адекватною;

б) обчислимо статистику:

Знайдемо відповідне табличне значення розподілу з ступенями свободи і рівнем значущості :

Оскільки , то можна зробити висновок про дос­товірність коефіцієнта кореляції, який характеризує тісноту зв'язку між залежною та незалежними змінними моделі.

Для вибраного рівня значущості і відповідного числа ступенів свободи запишемо довірчі межі для множинного кое­фіцієнта кореляції :

де

нижня межа довірчого інтервалу:

верхня межа довірчого інтервалу:

Отже, з імовірністю множинний коефіцієнт кореляції знаходиться в інтервалі

.

в) перевіримо значущість окремих коефіцієнтів регресії. Визначимо статистику за формулою

де — діагональний елемент матриці ; —стандартизо­вана похибка оцінки параметра моделі;

Експериментальні значення критерію порівнюємо з табличним з ступенями свободи і рівнем значущості :

Оскільки то відпо­відно оцінки є значущими, а оцінки не є значущими.

Обчислимо відношення

; ; ; .

(значення характеризують той факт, що оцінки – незміщені, а оцінки – зміщені);

4. Обчислимо коефіцієнти еластичності:

Коефіцієнт еластичності є показником впливу зміни питомої ваги на у припущенні, що вплив інших факторів відсутній: у нашому випадку він показує, що прибуток підприємства зменшиться на 0,1372 %, якщо інвестиції зростуть на 1%; прибуток підприємства зменшиться на 0,6997%, якщо витрати на рекламу зростуть на 1 %; прибуток підприємства збільшиться на 1,2310%, якщо заробітна плата зросте на 1 %.

Загальна еластичність від усіх факторів :

.

Загальна еластичність показує, що прибуток підприємства збільшиться на 0,3941%, якщо одночасно збільшити на 1 % кожний з факторів (інвестиції, витрати на рекламу та заробітну плату).

5. Побудуємо довірчі інтервали для параметрів регресії. Довірчі інтервали для параметрів обчислюються так:

де — діагональний елемент матриці помилок

; .

Результати розрахунків представлені в таблиці 3.2.

Таблиця 3.2

Межі прогнозних інтервалів параметрів моделі

Параметр моделі	Точкова оцінка	Гранична похибка	Межі прогнозних інтервалів
			Нижня межа	Верхня межа
	26,107885		4,306240	47,909531
	-0,2518005		-1,225163	0,721562
	-2,7276709		-9,176028	3,720686
	11,8560238		0,455428	23,256620

6. Обчислимо прогнозне значення прибутку підприємства (точковий прогноз) і знайдемо межі довірчого інтер­валів цього прогнозного значення (інтервальний прогнози):

а) для розрахунку точкового прогнозу у рівняння трьохфакторної лінійної регресії

підставимо прогнозні значення факторів

що лежать за межами базового періоду:

;

б) знайдемо межі інтервального прогнозу індивідуального значення (для ступенів свободи та вибраного рівня значущості за формулою:

,

де

Гранична похибка прогнозу:

.

Нижня межа прогнозного інтервалу:

.

Верхня межа прогнозного інтервалу:

.

Отже, прогнозне значення прибутку підприємства з імовірністю знаходиться у межах від 65,80404 млн. грн. до 95,54938 млн. грн.