§ 18. Центральная предельная теорема Ляпунова.

П.1. Сходимость по распределению.

Определение 18.1. Пусть F_n(x) – функция распределения случайной величины Х_n, где n = 1, 2, …, j, F(x) – функция распределения случайной величины Х. Говорят, что случайная последовательность {X_n} сходится к случайной величине Х по распределению при n  , если последовательность функций F_n(x) сходится к функции F(x) в каждой точке непрерывности функции F(x).

Этот вид сходимости обычно принято обозначать следующим образом

.

Если сравнивать сходимость по распределению со сходимостью по вероятности, то можно сделать следующий вывод

.

Обратное утверждение, вообще говоря, неверно.

Теорема 18.1. Характеристическая функция суммы независимых случайных величин Х₁, Х₂, …, Х_n равна произведению характеристических функций слагаемых.

Доказательство. Пусть g₁(t), g₂(t), …, g_n(t) – характеристические функции независимых СВ Х₁, Х₂, …, Х_n соответственно. Найдем характеристическую функцию СВ

.

Получим

= ,

поскольку Х₁, Х₂, …, Х_n – независимые СВ.

П.2. Центральная предельная теорема Ляпунова.

Многие из случайных явлений возникают благодаря действию большого числа случайных факторов, каждый из которых сам по себе незначительный. Одним из фундаментальных свойств природы является то, что при определенных (достаточно общих условиях) суммарное воздействие характеризуется случайной величиной с распределением близким к нормальному. Приведем математическое обоснование данному факту.

Рассмотрим совокупность независимых случайных величин Х₁, Х₂, …, Х_n. Составим из СВ Х₁, …, Х_n случайную величину Х:

,

где

.

Найдем М(Х) и (Х).

.

.

Таким образом, СВ Х является нормированной. В дальнейшем наша задача – изучить поведение Х при неограниченном увеличении составляющих ее СВ Х₁, …, Х_n.

Пусть для последовательности независимых СВ {X_n} n = 1, 2, … выполняется условие Ляпунова:

.

Условие Ляпунова можно пояснить следующим образом. Все слагаемые нормированной СВ Х равномерно малы в том смысле, что вероятность хотя бы одного из них превзойти величину  > 0 стремится к нулю при возрастании числа слагаемых. Другими словами, при увеличении числа случайных факторов, обуславливающих некоторое случайное явление, действие отдельно взятого фактора стремится к нулю.

Теорема 18.2. (Теорема Ляпунова) Если последовательность {X_n} n = 1, 2, … независимых СВ удовлетворяет условию Ляпунова и случайные величины X_n имеют конечные математические ожидания и дисперсии, то нормированная случайная величина Х сходится по распределению к случайной величине U, имеющей нормальное распределение с параметрами М(U) = 0, (U) = 1.

Доказательство. Найдем характеристические функции случайных величин: [X₁ – M(X₁)], [X₂ – M(X₂)], …, [X_n – M(X_n)].

Согласно определению,

.

Воспользуемся формулой разложения функции у = е^х в ряд Тейлора

,

где R₃(x) – остаточный член ряда Тейлора, для которого справедлива оценка

,

где С – некоторая постоянная, 0 <  < 1.

Разложим функцию g_k(t) в ряд Тейлора

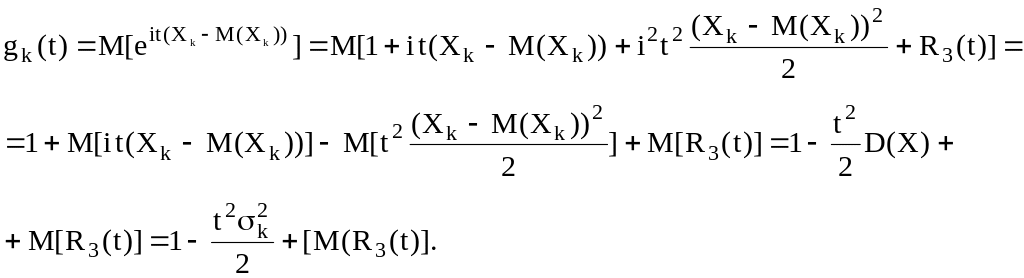Для остаточного члена M[R₃(t)] справедлива оценка:

,

где С – некоторая постоянная.

Характеристическая функция СВ Х будет иметь вид:

g_Х(t) = M[e^{i t X}] = .

Согласно теореме 18.1

g_Х(t) =

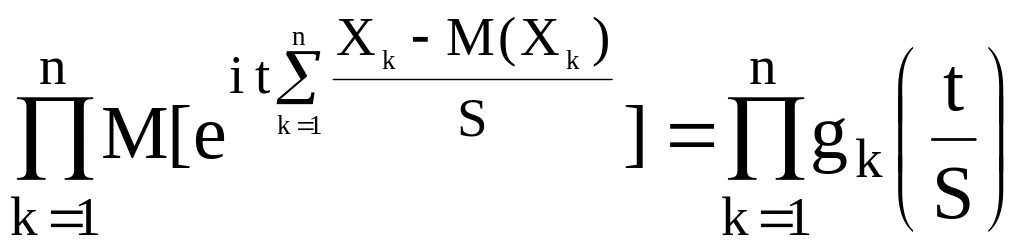
или, с учетом разложения в ряд g_k(t),

g_Х(t) = .

Прологарифмируем полученное равенство и воспользуемся приближенной формулой ln (1 + )  :

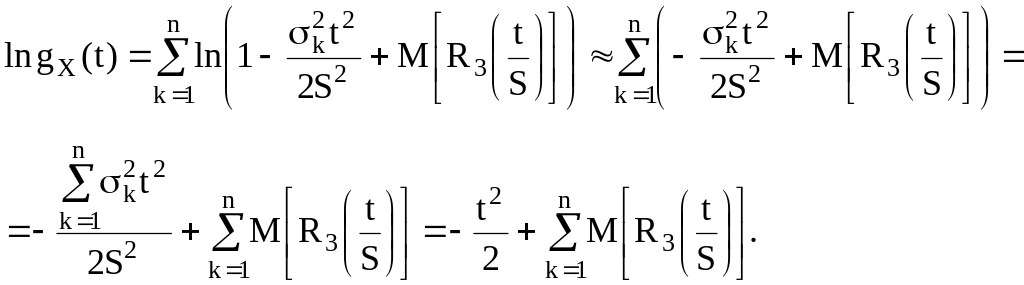
Согласно полученной оценке для остаточного члена и условия Ляпунова получим, что при n   , т.е. , и . Значит, g(t) = при n  .

Таким образом, характеристическая функция случайной величины Х при неограниченном возрастании числа n случайных факторов сходится к характеристической функции g(t) = нормально распределенной СВ с параметрами а = 0,  = 1.

Поскольку характеристическая функция однозначно определяет СВ Х, то СВ Х сходится по распределению к СВ U, имеющей нормальное распределение с параметрами М(U) = 1, (U) = 0, что требовалось доказать.

П.3. Теорема Муавра – Лапласа.

СВ Х₁, …, Х_n, фигурирующие в центральной предельной теореме, могут обладать произвольными распределениями вероятностей. Если считать, что все СВ Х_k одинаково распределены, дискретны и принимают только значения 0 или 1, то можно доказать важное для решения практических задач утверждение.

Теорема 18.3. (Теорема Муавра-Лапласа) Если производится n независимых опытов, в каждом из которых событие А появляется с вероятностью р, то для любого интервала (; ) справедливо соотношение

,

где Ф(х) – функция Лапласа, .

Доказательство. Проверим, что для независимых, одинаково распределенных СВ Х_k (k = 1,…), принимающих значение 0 или 1, причем Р(Х=1) = р, Р(Х = 0) = 1 – р = q, выполняется условие Ляпунова.

Проведем следующие преобразования

.

Учитывая, что	Xk	0	1	, получим
	pk	q	p

M[|X_k – M(X_k)| ³] = p|1 – M(X_k)| ³ + q |M(X_k)| ³ = p|1 – p| ³ + q  p ³ = pq(p² + q²).

Преобразуем следующее соотношение

.

Последние выражение стремится к нулю при n  . Следовательно, условие Ляпунова выполняется и СВ , где СВ U имеет нормальное распределение с параметрами М(U) = 0, ²(U) = 1.

Значит, при достаточно больших n справедливо соотношение

(данное утверждение называется локальной теоремой Муавра-Лапласа).

Из локальной теоремы Муавра-Лапласа можно получить оценку для вероятности Р( < X < ) (см. результаты § 9):

,

что требовалось доказать.

Важное практическое значение теоремы Муавра-Лапласа заключается в том, что для оценки вероятностей СВ, имеющей биномиальное распределение, можно использовать интегральную или локальную теорему Муавра-Лапласа, что гораздо проще использования формулы Бернулли при больших значениях n.

Несмотря на то, что центральная предельная теорема Ляпунова имеет достаточно глобальный природообъясняющий характер, существуют случаи, когда указанная теорема неприменима. Можно показать, что если вероятность р в схеме опытов Бернулли близка к нулю или к единице, то замена биномиального распределения на нормальное может дать большую ошибку на «хвостах» распределения, т.е. для значений СВ Х, удаленных от среднего значения.

Напомним, что если р мало, а n велико, то в схеме Бернулли можно получить другую оценку для Р(  Х  ). Согласно теореме Пуассона, при n p = a > 0

,

следовательно

Р(<Х < )  .

Таким образом для работы с биномиальным законом возможны два приближения, представленные в таблице 18.1.

Таблица 18.1.

Приближение	Рk(х)		Погрешность	Рекомендуемый диапазон применения
Пуассона			n p2	p  0 n p  10
Муавра-Лапласа				p >> 0 n p >> 10

Напомним, что в начале изложения курса теории вероятностей для числовой характеристики случайного явления было введено понятие частости или частоты, которая определялась после достаточно большого числа опытов. Дальнейшее использование понятия частоты для изучения свойств случайных явлений оказалось неудобным. Действительно, для решения любой даже несложной проблемы пришлось бы буквально «тонуть» в обилии различных опытов. В связи с этим было введено аксиоматическое определение вероятности. Опираясь на это определение, построен целый абстрактный мир со своими законами. В этом мире забывчивый студент не отличает одну страницу от другой, но четко помнит, что нужный ему номер двузначный; российские участники соревнований совершенно безвольно разбредаются по совершенно одинаковым номерам по велению совершенно бесстрастного портье; детали, поступившие из цехов, совершенно одинаковы, игральная кость обладает идеальной симметрией.

Многие события мы объявили несовместными или равновозможными на основании своей собственной интуиции. Наверняка у читателя появилось ощущение, что он имеет дело со сложной, хорошо отлаженной математической игрушкой-моделью.

Применима ли теория вероятностей на практике? На этот вопрос как раз и отвечают законы больших чисел. Оказывается, что при большом количестве опытов значения частоты и вероятности практически не отличаются, а большинство СВ в природе имеет нормальный закон распределения. Все это позволяет применить аппарат теории вероятностей не только для построения математических моделей, но и для сравнения этих моделей с реальностью. Этим мы займемся в следующем разделе.