
- •Глава 3. Законы больших чисел (случайные последовательности)
- •§ 16. Теорема Чебышева.
- •Рассмотрим выражение, стоящее во вторых скобках. Так как
- •Таким образом, справедливо неравенство
- •§ 17. Задачи для практического занятия по теме: «Теорема Чебышева и ее следствия».
- •§ 18. Центральная предельная теорема Ляпунова.
- •§ 19. Задачи для практического занятия по теме: «Центральная предельная теорема Ляпунова и ее следствия».
- •Проверочные вопросы.
- •Примеры для самостоятельного решения.
Глава 3. Законы больших чисел (случайные последовательности)
Законы больших чисел можно трактовать с двух позиций. По словам академика А.Н.Колмогорова, под законом больших чисел следует понимать утверждение: совокупное действие большого числа факторов приводит к результату почти не зависящему от случая.
В частном случае под законом больших чисел мы будем понимать совокупность утверждений, из которых следует приближение средних значений характеристик большого числа испытаний к некоторым определенным постоянным.
§ 16. Теорема Чебышева.
Прежде, чем перейти к формулировке центральной теоремы данного параграфа, рассмотрим несколько вспомогательных утверждений.
Лемма 16.1. (Неравенство Маркова) Если случайная величина Х принимает только неотрицательные значения и имеет математическое ожидание М(Х) = а, то для любого числа > 0 справедливо неравенство
Р(Х )
1 –
![]()
или
Р(Х > ) .
Доказательство. Доказательство проведем для дискретной СВ Х с заданным законом распределения
|
Х |
х1 |
х2 |
… |
хn |
|
|
р |
р1 |
р2 |
… |
рn |
|
Положим, что значения xi (i = 1, …, n) расположены в возрастающем порядке и выполняется условие: х1 , х2 , …, хk , xk+1 > , …, xn > .
Запишем выражение для математического ожидания СВ Х.
а = М(Х) = (х1р1 + х2р2 + … + хkрk) + (хk+1рk+1 + … + хnрn).
Рассмотрим выражение, стоящее во вторых скобках. Так как
хk+1рk+1 + … + хnрn М(Х) и xk+1 > , …, xn > ,
то
рk+1 + … + рn = (рk+1 + … + рn) М(Х).
Отсюда
рk+1
+ … + рn
![]() .
.
Значит P(X > ) = pk+1 + … + pn , что требовалось доказать.
Лемма 16.2. (Неравенство Чебышева) Пусть случайная величина Х имеет конечное математическое ожидание М(Х) = а и дисперсию D(Х). Тогда справедливо неравенство:
P(|X – a|
> )
![]() ,
,
где > 0.
Указанное неравенство можно переписать, используя свойство противоположного события,
P(|X – a| ) 1 – .
Доказательство. Для доказательства леммы 16.2 воспользуемся неравенством Маркова. Составим СВ (Х – а)2. Запишем неравенство Маркова для СВ (Х – а)2, взяв в качестве числа число 2.
P((X –
a)2
> 2)
![]() .
.
Учтем, что М((Х – а)2) = D(X), а также то, что из неравенства (Х – а)2 > 2 следует неравенство |X – a| > .
Таким образом, справедливо неравенство
P(|X – a| > ) ,
что требовалось доказать.
Для биномиально распределенной СВ Х неравенство Чебышева примет вид
P(|X
– рn|
> )
![]() или P(|X
– a|
)
1 –
.
или P(|X
– a|
)
1 –
.
(При выводе использовались соотношения а = р n, D = n p q.)
Из неравенства
Чебышева можно получить оценку доли
отклонения частости
![]() события в n
испытаниях, в каждом из которых оно
может произойти с вероятностью р, от
вероятности р:
события в n
испытаниях, в каждом из которых оно
может произойти с вероятностью р, от
вероятности р:
P(|
–
р|
)
1 –
![]() .
.
Неравенства Чебышева и Маркова имеют в основном теоретическое значение, поскольку для решения практических задач оценки, даваемые указанными неравенствами, довольно «грубые». Так, например, если M(X) > или D(Х) > 2, то неравенства Чебышева и Маркова примут вид
Р(Х ) 0 или Р(Х < ) 1
и
P(|X – a| ) 0 или P(|X – a| > ) 1.
Каждое из утверждений является очевидным и без использования указанных неравенств.
Прежде, чем сформулировать теорему Чебышева, дадим несколько определений.
Определение 16.1. Бесконечная последовательность случайных величин Хn, n = 1, 2,…, определенная на одном пространстве элементарных событий , называется случайной последовательностью (С.П.) и обозначается {Xn} n = 1, 2,….
Определение 16.2. Случайная последовательность {Xn} сходится по вероятности к случайной величине Х при n (Хn Х), если для всех > 0 справедливо
![]() или
или
![]() .
.
Теорема 16.1. (Теорема Чебышева) Если последовательность {Xn} образована независимыми случайными величинами, дисперсии которых ограничены одной и той же постоянной С, то при увеличении n средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий а1, а2, …, аn, т.е.
![]()
или
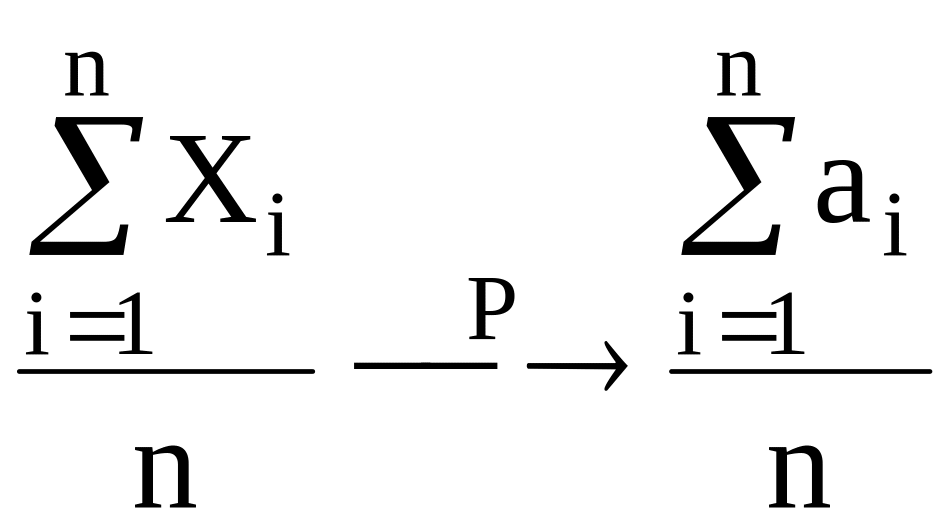 .
.
Доказательство. Введем в рассмотрение новую СВ Х
![]() .
.
Найдем математическое ожидание СВ Х

Найдем верхнюю оценку дисперсии D(X)

Запишем неравенство Чебышева для СВ Х
![]() .
.
При n
величина
![]() .
Поэтому
.
Поэтому
![]() .
.
Учитывая, что вероятность события не может превышать единицу, окончательно можно записать
,
что требовалось доказать.
Следствие 16.1. (Теорема Пуассона) Частость события в n повторных испытаниях, в каждом из которых оно может произойти с вероятностями р1, р2, …, рn, при неограниченном увеличении числа n сходится по вероятности к средней арифметической вероятностей в отдельных испытаниях, т.е.
 .
.
Теорема Пуассона следует из теоремы Чебышева, если в качестве СВ Х1, Х2, …, Хn рассматривать СВ, имеющие законы распределения вида:
0 |
1 |
, |
0 |
1 |
…, |
0 |
1 |
1 – р1 |
р1 |
1 – р2 |
p2 |
1 – рn |
pn |
В этом случае М(Х1) = р1, М(Х2) = р2, …, М(Хn) = рn.
Дисперсии СВ Х1,
…, Хn ограничены
числом
![]() .
Действительно,
.
Действительно,
![]() .
.
Применим теорему Чебышева

Если в условиях теоремы Пуассона р1 = р2 = … = рn, то получим следующее утверждение.
Следствие 16.2. (Теорема Бернулли) Частость события в n повторных независимых испытаниях, в каждом из которых оно может появиться с одной и той же вероятностью р, при неограниченном увеличении числа n сходится по вероятности к вероятности р этого события в отдельном испытании:
![]() .
.
Теорема
Чебышева. Основной смысл теоремы
Чебышева состоит в том, что для большого
числа СВ Х1, Х2,…,Хn,
случайная величина
 сколь угодно мало отличается от
неслучайной величины
сколь угодно мало отличается от
неслучайной величины
![]() .
.
Теорема Чебышева и ее следствия имеют практическое приложение. Она используется в самых различных областях народного хозяйства, а также в теории измерений.
Например, если
надо измерить некоторую величину,
истинное значение которой равно а,
проводят n независимых
измерений. Пусть результат каждого
измерения – СВ Хi
(i = 1, 2, …, n).
Если при измерении отсутствуют
систематические ошибки, то М(Хi)
= а. Тогда на основании теоремы Чебышева
![]() .
Значит, в качестве меры истинного
значения а следует взять среднее
арифметическое значение измерений.
.
Значит, в качестве меры истинного
значения а следует взять среднее
арифметическое значение измерений.
Пусть все измерения проводятся с одинаковой точностью – D(Хi) = 2, тогда
 ,
,
а
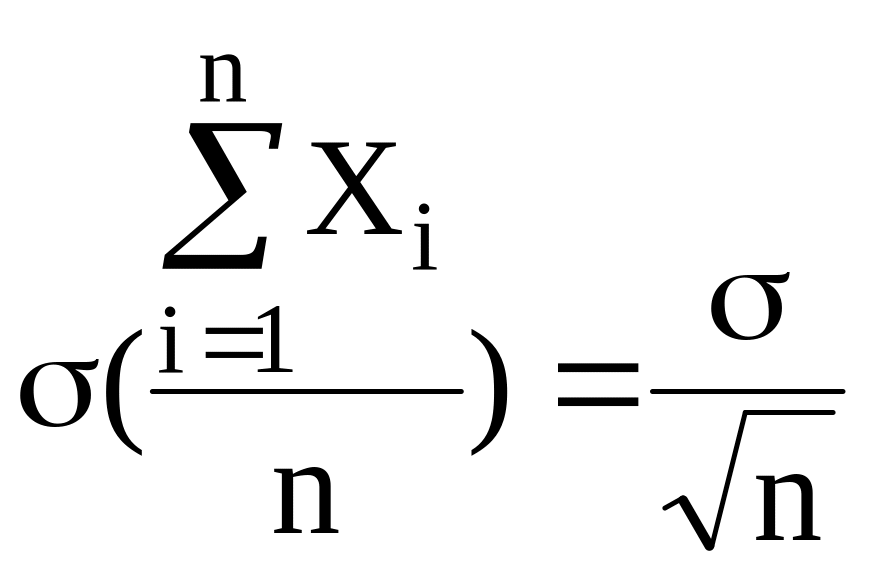 .
.
Полученные отношения известны как «правило корня из n», означают, что при увеличении числа опытов можно уменьшить влияние случайных погрешностей и, следовательно, увеличить точность измерений.
Исторически теорема Бернулли была доказана гораздо раньше теоремы Чебышева, но такое доказательство является достаточно громоздким. Теорема Бернулли дает теоретическое обоснование замены неизвестной вероятности события его частостью, полученной при достаточно большом числе испытаний.
