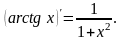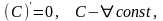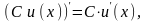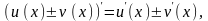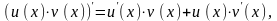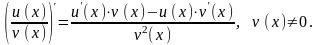Задание 8
Найти указанные пределы, не пользуясь правилом Лопиталя.
а) |
|
|
б) |
|
в) |
|
|
|
|
Решение:
а) Предел частного равен частному
пределов, если эти пределы существуют,
конечны и знаменатель не равен нулю. В
этом же примере в числителе и в знаменателе,
при подстановке вместо x
– бесконечности, получаем бесконечности.
В таких случаях говорят, что имеем
неопределенность вида 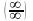 (бесконечность
делить на бесконечность). Для раскрытия
этой неопределенности целесообразно
выделить элементы, порождающие эти
бесконечности. Для этого и в числителе,
и в знаменателе вынесем за скобку степень
x
с наибольшим показателем. В результате
выражения в скобках будут стремиться
к конечным пределам, а степени x
за скобками сократятся. Решим данный
пример:
(бесконечность
делить на бесконечность). Для раскрытия
этой неопределенности целесообразно
выделить элементы, порождающие эти
бесконечности. Для этого и в числителе,
и в знаменателе вынесем за скобку степень
x
с наибольшим показателем. В результате
выражения в скобках будут стремиться
к конечным пределам, а степени x
за скобками сократятся. Решим данный
пример:
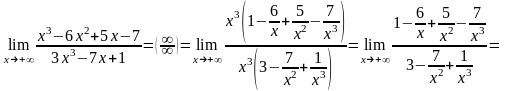
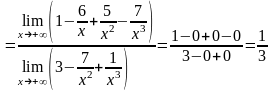 .
.
б)
В данном случае также не можем применить
теорему о пределе частного, так как
знаменатель стремиться к нулю. В числителе
и в знаменателе при подстановке x=1
получаем нули. В таких случаях говорят,
что имеем неопределенность вида 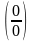 (ноль
делить на ноль). Для раскрытия этой
неопределенности целесообразно выделить
элементы, порождающие нули (возможно,
это будут множители вида (x–1)).
Для этого и числитель, и знаменатель
разложим на множители:
(ноль
делить на ноль). Для раскрытия этой
неопределенности целесообразно выделить
элементы, порождающие нули (возможно,
это будут множители вида (x–1)).
Для этого и числитель, и знаменатель
разложим на множители:
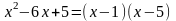 ,
,
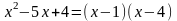 .
.
Подставляя соответствующие выражения и сокращая общий множитель (x–1), стремящийся к нулю, но не равный ему, получим
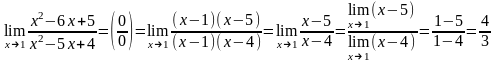 .
.
в)
В числителе и в знаменателе при подстановке
x=0
получаем нули. Имеем неопределенность
вида
.
Так как в примере присутствуют
тригонометрические функции, то для
раскрытия неопределенности можно
применить первый замечательный предел:
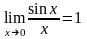 .
Преобразуем выражение под знаком
предела, используя тригонометрические
формулы:
.
Преобразуем выражение под знаком
предела, используя тригонометрические
формулы:

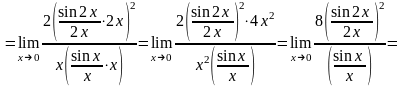
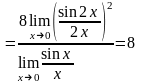 ,
так как
,
так как
 и
.
и
.
Задание 9
При нахождении производной заданных функций следует пользоваться таблицей производных основных элементарных функций, правилами дифференцирования и теоремой о дифференцировании сложной функции. Приведем некоторые формулы:
1.
|
6.
|
2.
|
7.
|
3.
|
8.
|
4.
|
9.
|
5.
|
10.
|
Правила дифференцирования:
Если
 т.е.
т.е.
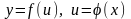 - сложная функция, то
- сложная функция, то
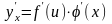
Примеры
Найти :
а)
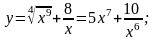
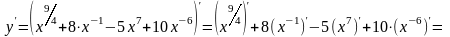
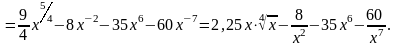
б)
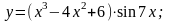
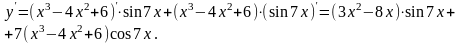
в)
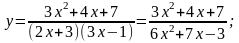
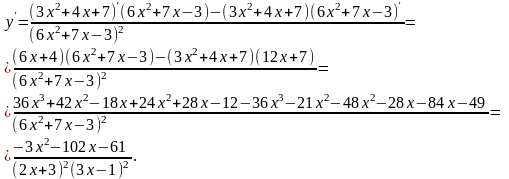
г)
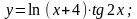
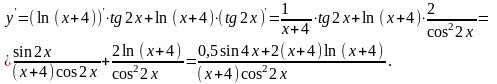
д)

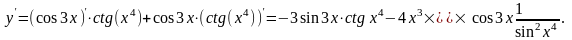
Задание 10
Дифференциальное
уравнение (ДУ) первого
порядка имеет вид
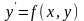 или
или
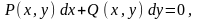 где
где
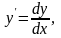 у
– искомая функция от переменной х,
у
– искомая функция от переменной х,
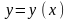 .
.
Процесс решения ДУ называется его интегрированием.
ДУ с разделяющимися переменными имеет вид
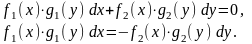 (1)
(1)
Пусть
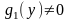 и
и
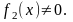 Разделим обе части уравнения (1) на
произведение
Разделим обе части уравнения (1) на
произведение
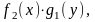 получим ДУ
с разделенными переменными
получим ДУ
с разделенными переменными
 (2)
(2)
Равенство (2) означает, что дифференциалы двух функций равны,, значит сами функции отличаются лишь на постоянное слагаемое. Интегрируя равенство (2), получим общее решение или общий интеграл ДУ (1)
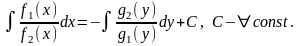
Пример: Проинтегрировать ДУ
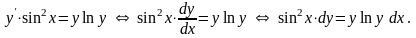
Разделим переменные и проинтегрируем обе части равенства
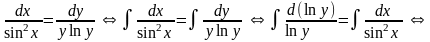
 -
общий интеграл
исходного ДУ, где
-
общий интеграл
исходного ДУ, где
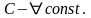

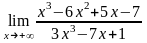 ;
;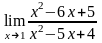 ;
;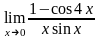 ;
;
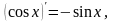
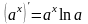
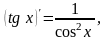
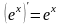

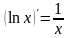 ,
,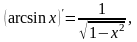
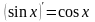 ,
,