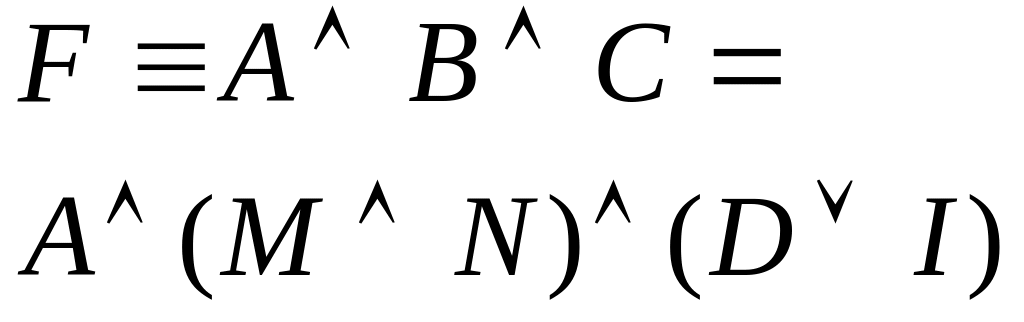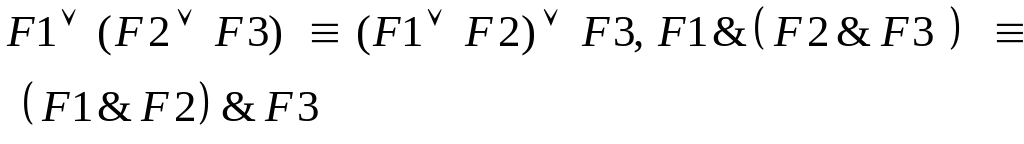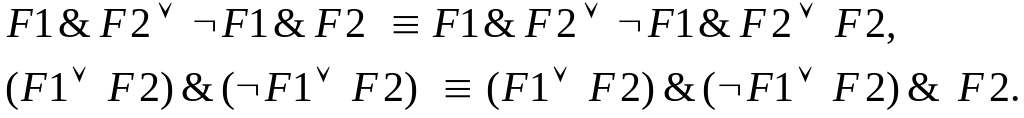3 Формалізація та алгоритмізація медичних задач в інформаційних системах

Специфіка роботи медичного співробітника з точки зору сучасних інформаційних технологій на базі персональних комп'ютерів полягає у виконанні великого обсягу неформальних дій. Слабко формалізована робота лікаря входить у протиріччя з сутністю інформаційних підходів. Хвороби схильні до природної мінливості. Зазвичай медичні задачі є слабкоструктуровані або неструктуровані.

Формалізація медичної, адміністративної та іншої діяльності лікувальних установ – те фундаментальне, що забезпечує побудову нової системи охорони здоров'я на базі повсюдного впровадження інформаційних систем.

Обчислювальні методи, які засновані на спробах алгоритмічного подання клінічних даних, застосовуються в медицині давно. Прикладами можуть бути акушерські календарі для визначення терміну вагітності, різні бальні методи, в яких кожному симптому приписується вага на основі клінічного досвіду. З поширенням ЕОМ у медицині стали розвиватися детерміністські підходи, в рамках яких кожне захворювання описувалося набором симптомів з альтернативним проявом і, відповідно, мало свій двійковий код. Реалізацією цього підходу є матричні алгоритми – найбільш прості способи автоматизації диференціальної діагностики. Суть їх – зіставлення набору симптомів пацієнта з наборами, характерними для різних захворювань, і встановлення діагнозу при їх співпадінні. Для ефективного використання таких методів необхідна чітка класифікація захворювань та опис симптомів, що однаково розуміється. Матричні алгоритми використовуються в навчальному процесі, зручні для навчання диференціальній діагностиці.

Алгоритмічний підхід у медицині зберігає свою актуальність. Нині це пов'язано зі світовою тенденцією до об'єктивізації процесів обстеження хворого та призначення лікування, тобто з розвитком доказової медицини.

Сучасний фахівець у галузі інформаційних технологій у медицині має володіти фундаментальними знаннями в області алгоритмізації. Під цим розуміється системний підхід до вирішення інформаційних завдань, алгоритмічне мислення, знання термінології та сучасних засобів розробки програмного забезпечення.

Двом аспектам, що мають важливе значення під час розробки МІС – формалізації медичних знань та алгоритмічному підходу до вирішення медико-біологічних задач, присвячений даний розділ.

3.1 Формалізація медичних знань

Формалізація (від лат. forma – вигляд, образ) – відображення результатів мислення в точних поняттях і твердженнях.

Багато медичних проблем не можуть бути не тільки вирішені, але навіть сформульовані, поки не будуть формалізовані міркування, які пов'язані з ними. Внаслідок аналізу задачі визначається специфіка даних, вводиться система умовних позначень, встановлюється належність її до одного з класів задач (наприклад, математичні, фізичні, медичні тощо).

Якщо деякі аспекти розв'язуваної задачі можна виразити в термінах якої-небудь формальної моделі (певної структури, яка використовується для подання даних), то це безумовно необхідно зробити, оскільки в цьому випадку в рамках формальної моделі можна дізнатися, чи існують методи і алгоритми вирішення поставленої задачі. Навіть якщо вони не існують, то використання засобів і властивостей формальної моделі допоможе в побудові розв'язку задачі.

Формалізація – це уявлення та вивчення якої-небудь змістовної області знання (наукові теорії, міркування, процедура пошуку тощо) у вигляді формальної системи або обчислення.

Людський організм вищою мірою складна функціональна система, про яку ми проте знаємо мало. Через брак інформації медичні знання мають вельми складну структуру, що ускладнює їх формалізацію.

Діагностичний процес у медицині побудований на міркуваннях про ознаки та їх сполучення, що обґрунтовують або відкидають певну діагностичну гіпотезу, фактично спирається на логіку аргументації.

Використання засобами формалізації як логіки об'єктивного знання, так і логіки суб'єктивного знання (логіки аргументації) може бути основою для доказовості дій лікаря, роблячи МІС більш зрозумілими для користувачів.

Клінічне мислення – це специфічна розумова свідома і підсвідома діяльність лікаря, яка дає можливість найбільш ефективно використовувати дані логіки й досвіду для вирішення діагностичних і терапевтичних задач щодо конкретного хворого.

На думку Є.І. Чазова [27], успіхи професійної лікувально-діагностичної діяльності зрештою визначаються логіко-методологічними можливостями мислення. Основні правила логічно стрункого лікарського мислення розкриваються в логічних законах.

3.1.1 Основні логічні закони

Серед безлічі логічних законів логіка виділяє чотири основних, які виражають корінні властивості логічного мислення – його визначеність, несуперечність, послідовність та обґрунтованість. Це закони тотожності, непротиріччя, виключеного третього і достатньої підстави. Вони діють у будь-якому розміркуванні, в якій би логічній формі воно не протікало і яку б логічну операцію не виконувало. Поряд з основними, логіка вивчає закони подвійного заперечення, де Моргана і багато інших, які також діють у мисленні, обумовлюючи правильний зв'язок думок у процесі розміркуванні.

Розглянемо основні логічні закони:

1) закон тотожності. Будь-яка думка в процесі розміркування повинна мати певний, стійкий зміст. Це корінна властивість мислення – ії визначеність – виражає закон тотожності: будь-яка думка в процесі розміркування має бути тотожна самій собі ( є , або , де під розуміється будь-яка думка) [28].

Із закону тотожності випливає: не можна ототожнювати різні думки, не можна тотожні думки приймати за нетотожні. Порушення цієї вимоги в процесі розміркування нерідко буває пов'язано з різним виразом однієї й тієї самої думки у мові.

Наприклад, два судження: «Пацієнт Н. отримав травму» і «Пацієнт Н. отримав пошкодження в організмі, викликане факторами зовнішнього середовища» – виражають одну й ту ж думку (якщо, зрозуміло, йдеться про одну й ту саму особу). Травма і є ушкодження в організмі людини або тварини, викликане факторами зовнішнього середовища. Тому було б помилковим розглядати ці думки як нетотожні.

З іншого боку, вживання багатозначних слів може привести до помилкового ототожнення різних думок. Наприклад, словом «рак» позначають хворобу, тварину класу ракоподібних, зодіакальне сузір'я, знак зодіаку. Очевидно, вживати подібне слово в одному значенні не слід.

Ототожнення різних думок нерідко пов'язано з відмінностями у професії, освіті тощо. Так буває під час вирішення медико-біологічних задач, коли фахівець з біоінженерії, який розробляє медичну інформаційну систему, не знаючи точного змісту деяких медичних понять, розуміє їх інакше, ніж лікар.

Ототожнення різних понять являє собою логічну помилку – підміну поняття, яка може бути як неусвідомленою, так і навмисною.

Дотримання вимог закону тотожності має важливе значення у роботі фахівця, яка вимагає вживання понять у їх точному значенні.

Під час вирішення медико-біологічних задач важливо з'ясувати точний зміст понять, якими користуються лікарі або пацієнти, і вживати ці поняття у суто певному сенсі;

2) закон непротиріччя. Логічне мислення характеризується непротиріччям. Протиріччя руйнують думку, ускладнюють процес пізнання. Вимога несуперечності мислення виражає формально-логічний закон непротиріччя: два несумісних один з одним судження не можуть бути водночас істинними; принаймні одне з них є хибним [28].

Цей закон формулюється так: невірно, що і не- (заперечення висловлювання ) водночас істинні (не можуть бути істинними дві думки, одна з яких заперечує іншу).

Закон непротиріччя діє відносно всіх несумісних суджень. Для правильного його розуміння необхідно мати на увазі наступне. Стверджуючи що-небудь про будь-який предмет, не можна, не суперечачи собі, заперечувати те саме про той самий предмет, взятий у той самий час і в тому самому відношенні.

Зрозуміло, що не буде протиріччя між судженнями, якщо в одному з них стверджується приналежність предмету однієї ознаки, а в іншому – заперечується приналежність цьому ж предмету іншої ознаки і якщо йдеться про різні предмети.

Цей закон прийнято називати законом протиріччя. Однак назва – закон непротиріччя – точніше виражає його дійсний зміст.

Протиріччя не буде і в тому випадку, якщо ми що-небудь стверджуємо і те саме заперечуємо щодо однієї особи, але розглянутої в різний час. Припустимо, що пацієнт Н. на початку хвороби мав супровідне захворювання, проте в кінці проведення лікувально-діагностичних заходів вилікувався від нього. У цьому випадку судження: «Пацієнт Н. має супровідне захворювання» і «Пацієнт Н. не має супровідного захворювання» – не суперечать одне одному.

Нарешті один і той самий предмет нашої думки може розглядатися в різних відносинах. Так, про студента Іванова можна сказати, що він добре знає англійську мову, оскільки його знання задовольняють вимогам, висунутим до вступників до університету. Проте цих знань недостатньо для роботи перекладачем. У цьому випадку ми маємо право сказати: «Іванов погано знає англійську мову». У двох судженнях знання Івановим англійської мови розглядається з точки зору різних вимог, отже, ці судження також не суперечать одне одному.

Класичним прикладом застосування закону непротиріччя в діагностичній практиці є ситуація, коли діагноз, встановлений під час клінічного обстеження хворого, не підтверджується лабораторно-інструментальними даними, на підставі чого лікар відкидає початковий діагноз та продовжує діагностичний пошук.

Закон непротиріччя виражає одне з докорінних властивостей логічного мислення – несуперечність, послідовність мислення. Його свідоме використання допомагає виявляти й усувати протиріччя в своїх та чужих розміркуваннях, виробляє критичне ставлення до будь-якої неточності, непослідовності в думках і діях;

3) закон виключеного третього. Закон непротиріччя діє відносно всіх несумісних один з одним суджень. Він встановлює, що одне з них є хибним. Питання про друге судження залишається відкритим: воно може бути істинним, але може бути й хибним [28].

Закон виключеного третього діє тільки відносно суджень, які суперечать (контрадикторних). Він формулюється так: два суперечливих судження не можуть бути водночас хибними, одне з них необхідно істинне: є або , або не- . Істинне або твердження деякого факту, або його заперечення.

Суперечним (контрадикторним) називаються судження, в одному з яких щось стверджується (або заперечується) про кожен предмет деякої множини, а в іншому – заперечується (затверджується) про деяку частину цієї множини. Ці судження не можуть бути водночас ні істинними, ні хибними: якщо одне з них істинне, то інше хибне і навпаки. Наприклад, якщо судження «Кожному громадянину України гарантується право на одержання кваліфікованої медичної допомоги» істинне, то судження: «Деяким громадянам України не гарантується право на одержання кваліфікованої медичної допомоги» – хибне. Суперечним є також два судження про один предмет, в одному з яких щось стверджується, а в іншому те саме заперечується. Наприклад: «Пацієнт П. знаходиться у стаціонарі» і «Пацієнт П. не перебуває у стаціонарі». Одне з цих суджень необхідно істинне, інше – необхідно хибне.

Подібно закону непротиріччя закон виключеного третього виражає послідовність, несуперечність мислення, не допускає протиріччя у думках. Разом з тим, діючи тільки відносно суперечливих суджень, він встановлює, що два суперечливих судження не можуть бути не тільки водночас істинними (на що вказує закон непротиріччя), але також і водночас хибними: якщо хибне одне з них, то інше необхідно істинне, третього не дано.

Звичайно, закон виключеного третього не може вказати, яке саме з даних суджень істинне. Це питання вирішується іншими способами. Значення закону полягає в тому, що він вказує напрямок у відшуканні істини: можливо тільки два вирішення питання, причому одне з них (і тільки одне) необхідно істинне.

Закон виключеного третього вимагає ясних, певних відповідей, вказуючи на неможливість відповідати на одне й те саме питання в одному й тому самому сенсі і «так» і «ні», на неможливість шукати щось середнє між затвердженням чого-небудь і запереченням того самого.

Необхідно чітко розрізняти суперечливі та протилежні поняття. Описуваний закон не діє під час аналізу протилежних понять. Вони заперечують один одного, але не вичерпують обсягу родового поняття, тобто не можуть бути водночас істинними, але можуть бути водночас хибними. Так, протилежні загально-стверджувальне та загально-негативне судження завжди будуть помилковими, наприклад: «Всі хвороби викликаються мікробами» і «Жодна хвороба не викликається мікробами». Істинним тут буде окреме судження: «Деякі хвороби викликаються мікробами». Нарешті, закон виключеного третього не діє під час оцінювання істинності порівнянних суджень. Наприклад, два несуперечливих одиничних судження: «У цього хворого пневмонія» і «У цього хворого бронхіт» можуть бути водночас й істинними і хибними, і використовувати тут закон виключеного третього невірно;

4) закон достатньої підстави. Думки про який-небудь факт, явище, подію можуть бути істинними або помилковими. Висловлюючи щиру думку, необхідно обґрунтувати її істинність, тобто довести її відповідність дійсності. Так, ставлячи заключний діагноз, лікар має привести необхідні докази, обґрунтувати істинність свого твердження. В іншому випадку діагноз буде необґрунтованим.

Вимога доведеності, обґрунтованості думки виражає закон достатньої підстави: будь-яка думка визнається дійсною, якщо вона має достатню підставу. Якщо є , то є й його підстава .

Лише наявність достатніх підстав робить, наприклад, медичний діагноз правильним, доведеним і достовірним. Цей закон лежить в основі процесу обґрунтування клінічного діагнозу.

Достатньою підставою думок може бути особистий досвід людини. Істинність деяких суджень підтверджується шляхом їх безпосереднього зіставлення з фактами дійсності.

Істинність законів, аксіом підтверджена практикою людства та не потребує тому нового підтвердження. Для підтвердження якого-небудь окремого випадку немає необхідності обґрунтовувати його за допомогою особистого досвіду. Якщо, наприклад, нам відомий закон Архімеда (кожне тіло, занурене в рідину, втрачає у своїй вазі стільки, скільки важить витіснена ним рідина), то немає жодного сенсу занурювати в рідину який-небудь предмет, щоб з'ясувати, скільки він втрачає у вазі. Закон Архімеда буде достатньою підставою для підтвердження будь-якого окремого випадку.

Таким чином, достатньою підставою будь-якої думки може бути будь-яка інша, вже перевірена і встановлена думка, з якої з необхідністю випливає істинність даної думки.

Якщо з істинності судження випливає істинність судження , то буде підставою для , – наслідком цієї підстави.

Зв'язок підстави й наслідку є відображенням у мисленні об'єктивних, у тому числі причинно-наслідкових зв'язків, які виражаються в тому, що одне явище (причина) породжує інше явище (наслідок). Однак це відображення не є безпосереднім. У деяких випадках логічна підстава може збігатися з причиною явища (якщо, наприклад, думка про те, що кількість травм при дорожньо-транспортних пригодах збільшилася, обґрунтовується вказівкою на причину цього явища – ожеледь на дорогах). Але найчастіше такого збігу немає. Судження «Нещодавно був дощ» можна обґрунтувати судженням «Дахи будинків мокрі»; слід протекторів автомобільних шин – достатня підстава судження «В даному місці пройшла автомашина». Тим часом мокрі дахи і слід, залишений автомашиною, – не причина, а наслідок зазначених явищ. Тому логічний зв'язок між підставою та наслідком необхідно відрізняти від причинно-наслідкового зв'язку.

Обґрунтованість – найважливіша властивість логічного мислення.

Алгоритми діагностики в даний час – це евристики, спроба наблизитися до найбільш здійсненого психологічного механізму оперативного мислення та інтуїції – тобто «після логічного стрибка». Однак при цьому не слід забувати про елементарні правила алгебри логіки, на яких будуються правильні логічні умовиводи.

3.1.2 Елементи алгебри логіки

Логіка – наука про закони і форми мислення.

Висловлювання (судження) – деяка пропозиція, яка може бути істинною (вірною) або хибною.

Затвердження – судження, яке потрібно довести або спростувати.

Міркування – ланцюжок висловлювань чи тверджень, певним чином пов'язаних один з одним.

Умовивід – логічна операція, внаслідок якої з одного або декількох даних суджень випливає (виводиться) нове судження.

Дедуктивна логіка Аристотеля та індуктивна логіка Бекона-Мілля склали основу загальноосвітньої дисципліни, яка протягом тривалого часу була обов'язковим елементом європейської системи освіти і складає основу логічної освіти в даний час.

Цю логіку прийнято називати формальною, оскільки вона виникла і розвивалася як наука про форми мислення. Її називають також традиційною, або аристотелівською логікою.

Формальна логіка вивчає форми мислення, виявляючи структуру, загальну для різних за змістом думок. Розглядаючи, наприклад, поняття, вона вивчає не конкретний зміст різних понять, а поняття як форму мислення, незалежно від того, які саме предмети мисляться в поняттях. Формальна логіка вивчає закони, що обумовлюють логічну правильність мислення, без дотримання якої не можна прийти до результатів, відповідних дійсності, пізнати істину.

Формальна логіка – наука, що займається аналізом структури висловлювань і доказів, звертає основну увагу на форму у відволіканні від змісту.

Логічний вираз – запис або усне твердження, до якого, поряд з постійними, обов'язково входять змінні величини (об'єкти). Залежно від значень цих змінних логічне вираження може приймати одне з двох можливих значень: ІСТИНА (логічна 1) або НЕПРАВДА (логічний 0).

Деякі з цих виразів, які є завжди істинними, оголошуються аксіомами (або постулатами). Вони складають базову систему посилань, виходячи з якої і користуючись певними правилами виведення, можна отримати висновки у вигляді нових виразів, які також є істинними.

Якщо перераховані умови виконуються, то говорять, що система задовольняє вимогам формальної теорії. Її так і називають – формальною системою (ФС). Система, побудована на основі формальної теорії, називається також аксіоматичною системою.

Формальна теорія має задовольняти таке визначення. Будь-яка формальна теорія , що визначає деяку аксіоматичну систему, характеризується:

- наявністю алфавіту (словника), ;

- безліччю синтаксичних правил, ;

- безліччю аксіом, що лежать в основі теорії, ;

- безліччю правил виведення, .

Обчислення висловлень та обчислення предикатів є класичними прикладами аксіоматичних систем.

3.1.3 Мова логіки

Для вирішення будь-якої проблеми людиною використовуються деяка мова і певний механізм отримання висновків. У певному сенсі мова логічної моделі є частиною звичайної розмовної мови. Однак це частина, що включає тільки чітко визначені синтаксичні та семантичні правила, яка оперує об'єктами, що легко формалізуються.

Мова – це знакова інформаційна система, що виконує функцію формування, зберігання та передачі інформації в процесі пізнання дійсності та спілкування між людьми.

Штучні мови – це допоміжні знакові системи, які створюються на базі природних мов для точної та економної передачі наукової та іншої інформації. Вони конструюються за допомогою природної мови або раніше побудованої штучної мови.

Мову, що виступає засобом побудови або вивчення іншої мови, називають метамовою, основною – мовою-об'єктом.

Штучні мови успішно використовуються і логікою для точного теоретичного й практичного аналізу розумових структур.

Одна з таких мов – мова логіки висловлень. Вона застосовується у логічній системі, званій обчисленням висловлювань, яка аналізує міркування, спираючись на істинні характеристики логічних зв'язок і відволікаючись від внутрішньої структури суджень.

Мова логіки висловлювань включає: алфавіт, визначення правильно побудованих виразів, інтерпретацію.

Алфавіт логіки висловлювань складається з таких символів:

1) символи для висловлювань: ... (пропозиційні змінні);

2) символи для логічних зв'язок:

_- – кон'юнкція (зв'язка «І»);

_- – диз'юнкція (зв'язка «АБО»);

_- – імплікація (зв'язка «якщо ..., то ...»);

_- – еквіваленція, або подвійна імплікація (зв'язка «якщо і тільки якщо ..., то ...»);

- – заперечення («невірно, що ...»).

Технічні знаки мови: (,)– ліва і права дужки.

Під висловом в алгебрі логіки розуміється оповідна пропозиція (судження), яка характеризується певним значенням істинності. У найпростіших випадках використовуються два значення істинності: «істинно» – «хибно», «так» – «ні», «1» – «0». Така алгебра логіки, в якій змінна може приймати тільки два значення істинності, називається бінарною алгеброю логіки Буля, або «Булевою алгеброю» (від імені творця алгебри логіки). Оповідна пропозиція, в якій йдеться про одну-єдину подію, називається простим висловлюванням. Наприклад, пропозиція: «Серце – орган людини» є просте висловлювання, пропозиція «Не смітити!» не є висловленням.

З одного або декількох висловлювань можна утворити нові висловлювання. Об'єднання простих висловлювань у складні проводиться без урахування сенсу цих висловлювань на основі логічних правил (операцій, функцій, зв'язок).

Функції бінарної алгебри логіки наведені у табл. А.1, в якій зібрані форми запису і найменування функцій, що зустрічаються в різних літературних джерелах.

Розглянемо приклад складання складного логічного вираження на основі інформації медичного характеру.

Припустимо, є якась база даних, що містить інформацію про пацієнтів. З цієї бази даних слід відібрати пацієнтів за такими ознаками: пацієнти – «чоловіки», вік – «старше 40, але молодше 60 років», з діагнозами – «гіпертонія», «гіпотонія», з метою проведення подальшої профілактики інфаркту міокарда.

З'ясуємо, в якій ситуації логічне вираження «пацієнти чоловіки, віком старше 40, але молодше 60 років, з діагнозами «гіпертонія», «гіпотонія»» є істинним. Розкладемо цей вираз на прості логічні вирази (табл. 3.1).

Таблиця 3.1 – Приклад складання складного логічного вираження на основі інформації медичного характеру

Висловлювання	Позначення	Операція	Результат
Пацієнт чоловічої статі		Проста	ІСТИНА
Вік> 40 років		Проста	ІСТИНА
Вік <60 років		Проста	ІСТИНА
Вік старше 40 років, але молодше 60 років			ІСТИНА

Продовження табл. 3.1

Діагнози «гіпертонія»		Проста	ІСТИНА
Діагнози «гіпотонія»		Проста	ІСТИНА
Діагнози «гіпертонія» або «гіпотонія»			ІСТИНА
Пацієнти чоловіки, віком старше 40 років, але молодші 60 років, з діагнозами «гіпертонія», «гіпотонія»			ІСТИНА

Для визначення істинності складного судження необхідно аналізувати значення істинності кожного простого висловлювання та обчислювати значення істинності кожної подформули, що входить у формулу цього судження.

Розглянемо основні правила запису складних суджень:

- кожне входження логічної зв'язки « » належить до пропозиціональної змінної або формули, наступній безпосередньо за логічною зв'язкою праворуч;

- кожне входження логічної зв'язки « » після розстановки дужок пов'язує пропозиціональні змінні або формули, які безпосередньо оточують логічну зв'язку;

- кожне входження логічної зв'язки « » після розстановки дужок пов'язує пропозиціональні змінні або формули, які безпосередньо оточують цю зв'язку тощо;

- у формулах немає двох логічних зв'язок, які стоять поруч – вони мають бути роз'єднані формулами;

- у формулах немає двох формул, які стоять поруч – вони мають бути роз'єднані логічною зв'язкою;

- логічні зв'язки за силою та значущістю впорядковані так: , , , , , тобто найсильнішою зв'язкою є заперечення, потім кон'юнкція, диз'юнкція, імплікація і, нарешті, еквівалентність.

Знання сили логічних зв'язок дозволяє опускати дужки, без яких очевидний порядок виконання операцій.

Приклад.

Нехай дана формула .

Знаючи силу логічних зв'язок, спростити запис формули так:

1) видалити зовнішні дужки формули, оскільки вони не визначають старшинство жодної операції:

2) видалити дужки, що охоплюють формулу імплікації, оскільки операція еквівалентності виконуватиметься тільки після виконання операції імплікації:

3) видалити дужки, що охоплюють формулу диз'юнкції, оскільки операція імплікації буде виконуватиметься тільки після виконання операції диз'юнкції:

4) видалити дужки, що охоплюють формулу заперечення, оскільки операція диз'юнкції виконуватиметься тільки після виконання операції заперечення:

Послідовність виконання операцій визначається силою логічних зв'язок: спочатку обчислити значення , потім , і, нарешті, .

Дві формули та називають рівносильними , якщо вони мають однакове значення «істина» або «неправда» за однакових наборів пропозиційних змінних. Якщо дві формули рівносильні , то вони еквівалентні між собою, тобто . І навпаки, якщо формули еквівалентні , то вони рівносильні .

Знання законів алгебри висловлювань дозволяє виконувати еквівалентні перетворення будь-якої правильно побудованої формули для заміни одних логічних операцій на інші, зберігаючи її значення для всіх наборів пропозиційних змінних. Закони алгебри висловлювань подані у табл. 3.2.

Таблиця 3.2 – Закони алгебри висловлювань

Ім'я закону	Рівносильні формули
Комутативності
Асоціативності
Дистрибутивності
Ідемпотентності
Виключеного
Протиріччя
де Моргана
Поглинання
Порецкого
Узагальненого склеювання
Доповнення
Константи

Логіка висловлювань – основний розділ сучасної логіки, що має широке застосування в різних сферах інтелектуальної діяльності людини. Разом з тим, оскільки в логіці висловлювань не враховується суб'єктивно-предикатна структура висловлювань та ряд інших змістовних положень, з її допомогою можна адекватно формалізувати значну частину змістовних міркувань, використовуваних людиною. З цією метою додатково до засобів логіки висловлювань використовуються засоби логіки предикатів і металогіки.

Мова логіки предикатів застосовується в логічній системі, званій обчисленням предикатів, яка під час аналізу міркувань враховує не тільки істинні характеристики логічних зв'язок, але і внутрішню структуру суджень.

Під обчисленням (або дедуктивною системою) розуміється система, в якій існує деяка кількість вихідних об'єктів (аксіом) та деяка кількість правил побудови (правил виведення) нових об'єктів з вихідних і вже побудованих. При цьому в обчисленнях (на відміну від алгоритмів) порядок застосування правил виведення може бути довільним.

Призначена для логічного аналізу міркувань, мова логіки предикатів структурно відображає і точно слідує за смисловими характеристиками природної мови. Основною смисловою (семантичною) категорією мови логіки предикатів є поняття імені.

Ім'я – це мовне вираження, яке має певний зміст, у вигляді окремого слова або словосполучення, що позначає або іменує який-небудь позамовний об'єкт. Ім'я як мовна категорія має, таким чином, дві обов'язкові характеристики або значення: предметне значення і смислове значення.

Предметне значення (денотат) імені – це один або безліч яких-небудь об'єктів, які цим ім'ям позначаються. Наприклад, денотатом імені «лікарня» в українській мові буде все різноманіття споруд, які цим ім'ям позначаються: цегляні, кам'яні; одноповерхові та багатоповерхові тощо.

Смислове значення (смисл, або концепт) імені – це інформація про предмети, тобто притаманні їм властивості, за допомогою яких виділяють безліч предметів. У наведеному прикладі змістом слова «лікарня» будуть такі характеристики будь-якої лікарні: 1) це споруда (будівля); 2) побудована людиною; 3) призначена для лікування.

Ім'я денотує, тобто позначає об'єкти тільки через зміст, а не безпосередньо. Мовне вираження, що не має змісту, не може бути ім'ям, оскільки воно не осмислено, а отже, і не опредмечено, тобто не має денотата.

Типи імен мови логіки предикатів, зумовлені специфікою об'єктів іменування та являють собою його основні семантичні категорії, це імена: предметів; ознак; пропозицій.

Імена предметів позначають одиничні предмети, явища, події або їх множини. Об'єктом дослідження в цьому випадку можуть бути як матеріальні (кров, серце, термометр), так і ідеальні (воля, мрія) предмети.

За складом розрізняють імена прості, які не включають інших імен (людина), та складні, що включають інші імена (орган людини). За денотатом імена бувають одиничні й загальні. Одиничне ім'я позначає один об'єкт і буває представлений у мові ім'ям власним (Гіппократ) або дається описово (найбільша ріка в Європі). Загальне ім'я позначає безліч, що складається більш ніж з одного об'єкта; у мові воно буває представлено прозивним ім'ям (закон) або дається описово (великий дерев'яний будинок).

Імена ознак – якостей, властивостей або відносин – називаються предикатами. У реченні вони зазвичай виконують роль присудка (наприклад, «бути червоним», «ходити», «давати», «лікувати» тощо). Число імен предметів, до яких належить предикат, називається його місцевістю. Предикати, що виражають властивості, які притаманні окремим предметам, називаються одномісними (наприклад, «кров червона»).

Предикати, що виражають відносини між двома і більше предметами, називаються багатомісними. Наприклад, предикат «лікувати» належить до двомісного («Іванов лікує Петрова»), а предикат «дарувати» – до тримісного («Батько дає нирку синові»).

Таким чином, предикат – вираз, який граматично має форму висловлювання, але містить змінні деяких підмножин, на яких вони визначені.

При заміні змінних елементами відповідної підмножини предикат звертається у висловлювання. Зазвичай змінна стоїть в предикативній частині речення, що лежить в основі висловлювання (наприклад, бути -м відділенням лікарні, де може приймати значення «терапевтичним», «хірургічним», «кардіологічним» і т. д.).

Але загалом можливі і предикати « – діагноз», де « – бронхіт», « – інфаркт» і т.д.).

Речення – це імена для виразів мови, в яких щось стверджується або заперечується. За своїм логічним значенням вони виражають істину або неправду.

Алфавіт мови логіки предикатів включає такі види знаків (символів) [28]:

1) ... – символи для одиничних (власних або описових) імен предметів; їх називають предметними постійними, чи константами;

2) … – символи загальних імен предметів, що приймають значення в тій чи іншій області; їх називають предметними змінними;

3) … – символи для предикатів, індекси над якими виражають їх місцевість; їх називають предикатними змінними;

4) … – символи для висловлювань, які називають пропозиційними змінними (від латинського propositio – «вислів»);

5) логічні зв'язки:

– кон'юнкція; – диз'юнкція; – імплікація;

– еквіваленція; – заперечення.

6) , – символи для кількісної характеристики висловлювань; їх називають кванторами.

За допомогою кванторів у мові предикатів формулюються які-небудь загальні твердження.

(перевернута літера – початкова літера англ. слова «all») – квантор спільності, символізує вираження – все, кожен, будь-який, завжди і т.п., (перевернута літера – початкова літера англ. слова «exist») – квантор існування, символізує вираження – деякий, інколи, буває, зустрічається, існує тощо, – квантор одиничності.

Технічні знаки мови: (,) – ліва і права дужки.

Інших знаків даний алфавіт не включає.

За допомогою наведеної логічної мови будується формалізована логічна система, звана обчисленням предикатів.

В обчисленні предикатів основним об'єктом є перемінне висловлювання (предикат), істинність або хибність якого залежить від значень вхідних у нього змінних. Так, істинність предиката «х був лікарем» залежить від значення змінної . Якщо – це М. Амосов, то предикат істинний, якщо – М. Лермонтов, то він хибний [29].

Твердження читається так: «для всіх має місце », а твердження – як «існує таке, що », де і – предикати. Під час підстановки замість змінної « » будь-якого символу (наприклад, ), відповідного конкретному об'єкта реального світу, дорівнює значенню «істина».

Наприклад, твердження «всі хворі принаймні один раз у житті скаржилися на своє здоров'я» можна записати як:

де – предикатний символ, що означає їх пред'явлення.

Твердження означає «існує таке , для якого виконується », тобто існує принаймні один випадок істинності , як мінімум один об'єкт , під час підстановки якого .

Наприклад, твердження «існує людина, яка нічим не хворіє» можна записати як:

означає є тільки одне , таке, що буде .

Змінні, які входять у формулу з кванторами, називаються пов'язаними, не пов'язані кванторами змінні називаються вільними. Порядок застосування до змінних кванторів відповідає звичайному напрямку читання тексту – зліва направо.

Наприклад, розглянемо предикат , що описує відношення «захворювання x лікується препаратом y». Тоді, застосовуючи квантори, можна записати такі формули:

- – означає «будь-яку хворобу можна вилікувати чим завгодно»;

- – означає «цю хворобу можна вилікувати будь-яким препаратом»;

- – означає «цей препарат – панацея від усіх хвороб»;

- – означає «існує хвороба, яку можна вилікувати цим препаратом».

В обчисленні предикатів, як і в обчисленні висловів, існує поняття – формула.

В обчисленні висловлювань формули будуються індуктивним способом (індукція – це спосіб мислення від окремого до загального), використовуючи логічні зв'язки: (кон'юнкція), (диз'юнкція), (імплікація), (заперечення). Прикладами формул можуть бути:

де – висловлювання.

Обчислення предикатів включає в себе всі формули обчислення висловлювань, а також формули, що містять крім символів висловлювань предикатні символи з кванторами.

Виділена підмножина тотожна істинним формулам, істинність яких не залежить від істинності вхідних у них висловлювань, називається аксіомами.

Логіка предикатів спочатку не пов'язана з предметною областю. Семантика логіки предикатів – це внесення змісту в абстракцію моделі шляхом зіставлення її елементів з реаліями навколишнього світу. Встановлення відповідності між елементами мови предикатів та елементами предметної області (відображення знань) називається інтерпретацією.

Сутністю мови предикатів є можливість оцінки значення логічних формул на основі формул, які були раніше оцінені, тобто отримання висновків з посилань.

Значення формул оцінюються відповідно до таких правил:

- якщо істинність логічних формул і відома, то значення формул і т.д. оцінюються за таблицею істинності;

- якщо для всіх констант формула оцінена як «істина», то істинною є формула ;

- якщо хоча б для одного значення x формула істинна, то формула теж істинна.

У логіці предикатів забезпечується автоматична процедура дедуктивного виведення (отримання висновку, доведення теорем) шляхом застосування правил виведення до вихідної групи формул. Для цього в модель додається ще одна множина – множина формул, істинних за будь-якої інтерпретації (аксіом). Ці формули часто використовуються як вихідні під час обчислення істинності інших формул.

В обчисленні предикатів є безліч правил виведення. Як приклад наведемо два правила:

1. modus ponens (пряме доведення):

_.

Читається так: «якщо істинна формула та істинно, що з випливає , то істинна формула ». Формули, які знаходяться над рискою, називаються посиланнями виведення, а під рискою – висновком. Це правило виведення формалізує основний закон дедуктивних систем: з істинних посилань завжди випливають істинні висновки.

Нехай судження має вигляд: «Петров є лікарем», а судження – «У Петрова є диплом лікаря». Відповідно до правила modus ponens, якщо , то і , оскільки якщо істинно, що «Петров є лікарем», то також істинно, що «У Петрова є диплом лікаря». Іншими словами, з істинності умови та імплікації (судження над рискою) випливає істинність висновку (судження під рисою);

2. правило modus tollens визначається такоюсхемою виведення:

.

Продовжуючи приклад, можна зрозуміти, що якщо «У Петрова немає диплома лікаря», тобто , то «Петров не є лікарем», тобто . У цьому прикладі теж з істинності умови та імплікації випливає істинність висновку.

Аксіоми та правила виведення обчислення предикатів першого порядку задають основу формальної дедуктивної системи, в якій відбувається формалізація схеми міркування у логічному програмуванні.

Логіка предикатів 1-го порядку відрізняється від логік вищих порядків тим, що в ній заборонено використовувати вирази (формули) як аргументи предикатів.

Розглянута задача подається у вигляді тверджень (аксіом) числення предикатів першого порядку.

Мета задачі В також записується у вигляді твердження, справедливість якого випливає встановити або спростувати на підставі аксіом і правил виведення формальної системи. Тоді вирішення задачі (досягнення мети задачі) зводиться до з'ясування логічного слідування (виведення) цільової формули В із заданої множини формул (аксіом) Таке з'ясування рівносильно доведенню загально-значності (тотожно – істинності) формули або не здійснимості (тотожно – неправді) формули [29].

З практичних міркувань зручніше використовувати доведення від протилежного, тобто доводити нездійсненність формули. Цільове твердження інвертується, додається до множини аксіом і доводиться, що отримана таким чином множина тверджень є несумісною (суперечливою).

На доказі від противного засноване провідне правило висновку, використовуване в логічному програмуванні, – принцип резолюції. Під час використання його формули обчислення предикатів за допомогою нескладних перетворень приводяться до так званої диз'юнктивної форми, тобто подаються у вигляді набору диз'юнктів. При цьому під диз'юнктом розуміється диз'юнкція літералів, кожен з яких є або предикатом, або запереченням предиката.

Наведемо приклад диз'юнкта:

(3.1)

Нехай предикат – поважати, предикат – знати, константа – Іванов, а константа – біоінженерія.

Тоді вираз (3.1) перепишеться:

(3.2)

Диз'юнкти, які використовуються в логічному програмуванні, можна спростити так: квантори загальності опустити, предикати переписати без дужок, а зв'язку замінити на імплікацію ( ) або слово «якщо». Тоді вираз (3.2) набуде такого вигляду:

що читається так: «кожен, хто знає біоінженерію, поважає Ключевського». Крім того, диз'юнкти, всі літерали яких негативні, зазвичай переписуються в еквівалентну форму негативної кон'юнкції. Наприклад, формула перепишеться у вигляді:

(3.3)

Якщо у формулі (3.3) прийняти, що предикат – це «знати», а константи і – це «медицина» та «біоінженерія» відповідно, то отримаємо:

(3.4)

Вираз (3.4) у спрощеному вигляді можна переписати як:

і прочитати як запит: «хто знає медицину та біоінженерію водночас?».

Таким чином, і умови вирішуваних задач (факти), і цільові твердження задач (запити) можна виразити в диз'юнктивній формі логіки предикатів першого порядку.

Повернемося до принципу резолюції [30]. Головна ідея цього правила виведення полягає в перевірці того, чи містить множина диз'юнктів порожній (помилковий) диз'юнкт . При позитивній відповіді множина (і відповідна йому формула) нездійсненна (суперечлива). При негативній відповіді виводяться нові диз'юнкти до тих пір, поки не буде отриманий порожній диз'юнкт, що завжди матиме місце для суперечливого . Таким чином, принцип резолюції можна розглядати як правило виведення, за допомогою якого породжуються нові диз'юнкти з . У загальному випадку кожен крок резолюції починається з деякої пари диз'юнктів (предків) такої, що деякий літерал в одному з диз'юнктів має бути зроблений додатковим літералу іншого диз'юнкта з пари. Зауважимо, що додатковими називаються літерали і .

Щоб зробити літерали і додатковими, необхідно провести їх уніфікацію, тобто зробити їх ідентичними за допомогою деякої підстановки , званої уніфікатором: . Тоді говорять, що два обраних літерала резолюють. Потім за допомогою правила резолюції виводиться новий диз'юнкт – резольвента – таким чином. Літерали диз'юнктів-предків, за винятком тих, які резолювали, об'єднуються та до результату застосовується підстановка .

Наведемо приклад:

перший предок (диз'юнкт): Петро поважає

другий предок (диз'юнкт): поважає Івана, якщо батько (Іван) поважає

резолюючі літерали: те, що підкреслено

уніфікатор:

резольвента: батько (Іван) поважає Петро

Останнє твердження (резольвента) читається як «батько Івана поважає Петра?»

Правило резолюції має властивість повноти в тому сенсі, що за допомогою нього завжди можна знайти порожній диз'юнкт, якщо вихідна множина диз'юнктів суперечлива. Однак внаслідок нерозв'язності логіки предикатів першого порядку для здійсненної (несуперечливої) множини диз'юнктів процедура, заснована на принципі резолюції, може працювати нескінченно довго.

Зазвичай резолюція застосовується в логічному програмуванні в сукупності з прямим або зворотним методом міркування. Прямий метод (від посилань) з посилань виводить висновок (правило modus ponens). Основний недолік прямого методу міркування полягає в його ненаправленості: повторні застосування методу зазвичай призводять до різкого зростання проміжних висновків, не пов'язаних з цільовим висновком.

Зворотний метод (від мети) є спрямованим: з бажаного висновку і тих самих посилань він виводить новий підцільовий висновок . Кожен крок виведення в цьому випадку завжди пов'язаний з початково поставленою метою. Для використання правила резолюції необхідне, доведення того, що дане посилання тягне бажаний (цільовий) висновок , переформулювати в твердження, що несумісне з . Наприклад, щоб довести твердження з посилань , зворотне міркування за допомогою правила резолюції виводить (из і ), а потім виводить порожній диз'юнкт (спростування) (з і ).

Істотний недолік принципу резолюції полягає у формуванні на кожному кроці виведення безлічі резольвент – нових диз'юнктів, більшість з яких виявляються зайвими. У зв'язку з цим розроблені різні модифікації принципу резолюції, що використовують більш ефективні стратегії пошуку і різного роду обмеження на вид вихідних диз'юнктів. У цьому сенсі найбільш вдалою та популярною системою є система PROLOG, яка використовує спеціальні види диз'юнктів, звані диз'юнктами Хорна. Стисло розглянемо цю систему, тим більше що під логічним програмуванням у вузькому сенсі слова зазвичай розуміють програмування мовою PROLOG (PROgramming in LOGic).

За визначенням, диз'юнктами Хорна є диз'юнкти, які мають не більше одного позитивного літерала. Вони можуть бути трьох типів:

1) допущеннями без умов (чи фактами)

Наприклад, Івану подобається біоінженерія;

2) умовними допущеннями (або імплікаціями) – правилами

,

або в еквівалентній формі

Наприклад, Петро поважає , якщо х подобається логіка Петро знає ;

3) запереченнями

або

або

Наприклад, ( подобається логіка подобається математика).

Для реалізації дуже важливий той факт, що диз'юнкти Хорна володіють простою процедурною інтерпретацією. Диз'юнкти типу (1) і (2) інтерпретуються як процедури, а типу (3) – як цільові твердження. Так, диз'юнкт типу (2) інтерпретується як процедура із заголовком , тілом якої є виклик процедур , а диз'юнкт типу (3) – як послідовність викликів процедур . Тоді кожен крок зворотного міркування є управління викликом процедури, яке починається з виділення виклику деякої процедури з поточної мети. Потім виділяється деяка процедура, заголовок якої (позитивний літерал, наприклад ) у виразі (2)) уніфікується за допомогою деякої підстановки з обраним викликом .

Далі виділяється тіло процедури (в даному прикладі ), що являє собою, в свою чергу, послідовність виклику інших процедур (у даному прикладі . Уніфікатор застосовується до результату. Процес ітеративно повторюється. Аргументи літералів (предикатів) відповідають параметрам викликаних процедур. Уніфікація інтерпретується як зв'язок даних між викликами і процедурами.

Процес доведення (або обчислення) цільового твердження у загальному випадку можна подати так [31].

Нехай цільове твердження має вигляд та в ньому виділений літерал і нехай існує правило . Тоді якщо – уніфікатор для літералів і , то говорять, що підціль виводиться з за допомогою правила та підстановки .

Отримання з є елементарним кроком у мові PROLOG. Він може завершитися і невдачею, оскільки може не існувати уніфікатора для і .

Висновком (обчисленням) цільового твердження S називається послідовність проміжних під цілей , така, що і виведена з . Якщо з підцілі не виведена жодна підціль, то обчислення вважається кінцевим. При цьому якщо – не порожній диз'юнкт, то висновок є тупиковим, а якщо – порожній диз'юнкт, то висновок є успішним і з ним пов'язується підстановка , де – підстановка, за допомогою якої виведена підціль з .

Висновок мети зручно подавати у вигляді дерева І/АБО з коренем у цільовій вершині. Нагадаємо, що під деревом розуміється графова структура (тобто структура, яку можна зобразити у вигляді вершин і зв'язків), будь-які вершини-нащадки якої мають не більше однієї вершини-предка. Вершині типу дерева відповідає кон'юнкція умов деякого правила (тобто ), вершині типу АБО відповідає варіант, коли до одного і того самого висновку (резольвенти) наводять різні правила.

У будь-якій системі логічного програмування, в тому числі і в системі PROLOG, реалізується деяка стратегія обходу дерева пошуку, тобто використовується та чи інша вбудована у систему стратегія пошуку вирішення задачі. Переважно ці стратегії мають послідовний характер. Останнім часом починають з'являтися реалізації стратегій паралельного типу. Вони різко підвищують ефективність систем логічного програмування.

Найбільш поширеною стратегією послідовного типу є стратегія «спочатку в глибину». При цьому дерево пошуку упорядковується за допомогою двох лінійних порядків: «зліва направо» для літералів цілі типу (3) і «зверху вниз» для правил типу (1), (2). Тоді на кожному кроці пошуку виділеним виявляється перший зліва літерал мети і до нього застосовуються перше зверху правило. При цьому запам'ятовуються різні розгалуження. Якщо пошук заходить у глухий кут, то відбувається повернення до місця останнього розгалуження за допомогою механізму backtracking. Водночас скасовуються результати всіх підстановок, зроблених після цього розгалуження. Повернення здійснюється також і при успішному результаті для отримання інших відповідей. Робота закінчується, коли список розгалужень порожній. Основна перевага цієї стратегії – простота її реалізації, недолік – великий перебір для деяких класів підцілей. Крім того, якщо дерево пошуку містить нескінченну гілку, то потрапивши в неї, система не вийде звідти і правильні відповіді, що знаходяться правіше цієї мети на дереві, не будуть отримані.

Під час стратегії «спочатку в ширину» дерево пошуку обходить ярус за ярусом зверху вниз. Вона гарантує знаходження рішення, якщо воно існує. Однак стратегія вимагає значно більшого обсягу пам'яті і тому набула порівняно невеликого поширення.

Одна з переваг мов логічного програмування полягає в тому, що на їх основі досить зручно реалізувати стратегії паралельного типу, причому порядок обходу дерева не настільки важливий; істотний лише той факт, що має бути обійдене все дерево. Саме остання обставина і дає принципову можливість вести пошук паралельно. Зазвичай розрізняють два типи паралелізму: АБО-паралелізм, який означає одночасне застосування для виділеної підцілі з мети всіх правил з бази знань, та І-паралелізм, що означає паралельну обробку водночас усіх літералів (підцілей) цільового твердження. Крім того, паралелізм можливий і необхідний при уніфікації (оскільки ця операція застосовується часто). Найбільші перспективи мають саме паралельні стратегії, але для їх ефективної реалізації необхідні відповідні процесори, які використовують принципи паралельної архітектури.

Перевагою розглянутого логічного підходу є безпосереднє програмування механізму виведення, засноване на обчисленні значень складних логічних функцій, за якими з відомих знань можна отримати нові, а також чітка логіка і семантика.

Однак остання властивість є водночас і недоліком. Записати знання у вигляді логічних формул не вдається в тих випадках, коли ускладнений вибір констант, предикатів, функцій, або ж можливості подання у логіці предикатів недостатні для опису знань. Це може бути пов'язано, наприклад, з нечіткістю природної мови, яка в медичних предметних областях зустрічається дуже часто.

3.1.4 Основні поняття нечіткої логіки

Під час спроби формалізувати людські знання дослідники стикнулися з проблемою, яка ускладнює використання традиційного математичного апарату для їхнього опису. Існує цілий клас описів, які оперують якісними характеристиками об'єкта (багато, мало, дуже мало). Для вирішення таких проблем на початку 70-х років американський математик Лотфі Заде запропонував апарат нечіткої (fazzy) логіки. Пізніше цей напрямок поклав початок однієї з гілок штучного інтелекту під назвою м'які обчислення (soft computing).

Математична теорія нечітких множин (fuzzy sets) та нечітка логіка (fuzzy logic) є узагальненнями класичної теорії множин і класичної формальної логіки.

Основною причиною появи нової теорії стала наявність нечітких і наближених міркувань під час опису людиною процесів, систем, об'єктів.

Перш ніж нечіткий підхід до моделювання складних систем отримав визнання у всьому світі, минуло не одне десятиліття з моменту зародження теорії нечітких множин. І на цьому шляху розвитку нечітких систем прийнято виділяти три періоди.

Перший період (кінець 60-х – початок 70 рр..) характеризується розвитком теоретичного апарату нечітких множин (Л. Заде, Е. Мамдані, Беллман). У другому періоді (70-80-ті роки) з'являються перші практичні результати в області нечіткого управління складними технічними системами (парогенератор з нечітким керуванням). Водночас стала приділятися увага питанням побудови експертних систем, побудованих на нечіткій логіці, розробці нечітких контролерів. Нечіткі експертні системи для підтримки прийняття рішень знаходять широке застосування в медицині. Нарешті, в третьому періоді, який триває з кінця 80-х років і продовжується дотепер, з'являються пакети програм для побудови нечітких експертних систем, а області застосування нечіткої логіки помітно розширюються. Тріумфальний хід нечіткої логіки по світу почався після доведення в кінці 80-х Бартоломеєм Косько знаменитої теореми FAT (Fuzzy Approximation Theorem).

3.1.4.1 Поняття нечіткої множини

Предметною областю або повною множиною називатимемо сукупність досліджуваних об'єктів або елементів, розглянутих спільно. При цьому через позначатимемо окремі структурні елементи повної множини.

Нехай – деяка множина, визначена на повній множині . Характеристичною функцією множини називається функція, що визначає умови, яким має задовольняти структурний елемент , щоб належати множині .

Множина А називається чіткою множиною, якщо ії характеристична функція (функція приналежності) може приймати одне з двох можливих значень: , якщо ; , якщо .

Таким чином, чітка множина дозволяє однозначно розділити всі структурні елементи предметної області в залежності від наявності або відсутності в них будь-яких властивостей, що задаються цією множиною.

Приклад чіткої множини. Нехай повний простір позначає сукупність людей. Тоді визначимо множину , наприклад, як множину чоловіків (або множину жінок). Очевидно, що таким чином певна множина – чітка множина, оскільки вона формує статеву ознаку, що дозволяє однозначно розділити всі структурні елементи на дві групи.

Однак у реальному світі не завжди вдається однозначно розділити структурні елементи, використовуючи характеристичну функцію, що визначає наявність або відсутність заданої властивості або ознаки двома рівнями (1 або 0; «так» – «ні»). Наприклад, нехай як і раніше повний простір позначає сукупність людей. Визначимо множину – привабливий чоловік (або чарівна жінка). Очевидно, що зміст цього визначення нам зрозумілий, але сказати однозначно, чи належить конкретний чоловік або конкретна жінка до множини , тільки за допомогою понять «так» – «ні» дуже складно.

Тобто в даному випадку ми маємо справу з нестрогими властивостями досліджуваних об'єктів, що задаються нечіткою множиною .

Зауважимо, що подібна нечіткість задання ознак досліджуваних об'єктів є досить поширеною в діагностичній практиці. Наведемо як приклад перелік симптомів, використовуваних у процесі діагностики спадкових захворювань: «великий, виступаючий живіт», «високе небо», «аркоподібне небо» тощо. Зрозуміло, що наведені симптоми являють собою нечіткі поняття, оскільки не конкретизується, яким має бути живіт, щоб його можна було класифікувати як «великий, виступаючий».

Множина , що задається характеристичною функцією , називається нечіткою множиною, якщо ії характеристична функція, яка визначена на повній множині , може приймати будь-яке значення в інтервалі [0,1].

Тобто визначення нечіткої множини можна інтерпретувати так: величина функції приналежності визначає суб'єктивну оцінку ступеня приналежності деякого структурного елемента множині .

Чим більше аргумент відповідає нечіткій множині , тим більше значення , тобто тим ближче значення аргументу до 1.

Повернемось до використаного нами прикладу. означає, що конкретний чоловік (жінка) за своїми якостями потрапляє під визначення «чарівного» чоловіка (жінки), але водночас має деякі якості, які повною мірою не відповідають цьому поняттю.

Проілюструємо ще один приклад. Формалізуємо неточне визначення «гарячий лікувальний настій». Як x (область міркувань) виступатиме шкала температури у градусах Цельсія. Очевидно, що вона змінюватиметься від 0 до 100 градусів. Нечітка множина для поняття "гарячий лікувальний настій" може мати такий вигляд:

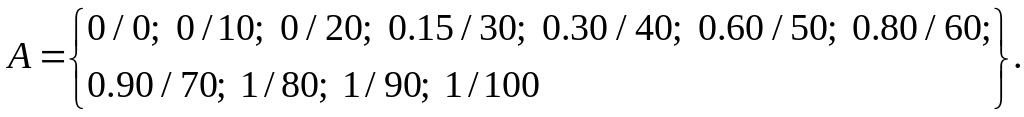
Так, настій з температурою 60 ^oС належить до множини «Гарячий» зі ступенем приналежності 0.80. Для однієї людини настій при температурі 60 ^oС може виявитися гарячим, для іншої – не надто гарячим. Саме в цьому і виявляється нечіткість задання відповідної множини.

Розглянемо часто використовувані стандартні форми функцій приналежності та їх графічні інтерпретації [32].

1. Функція приналежності класу сінглтон (англ. singleton) визначається як:

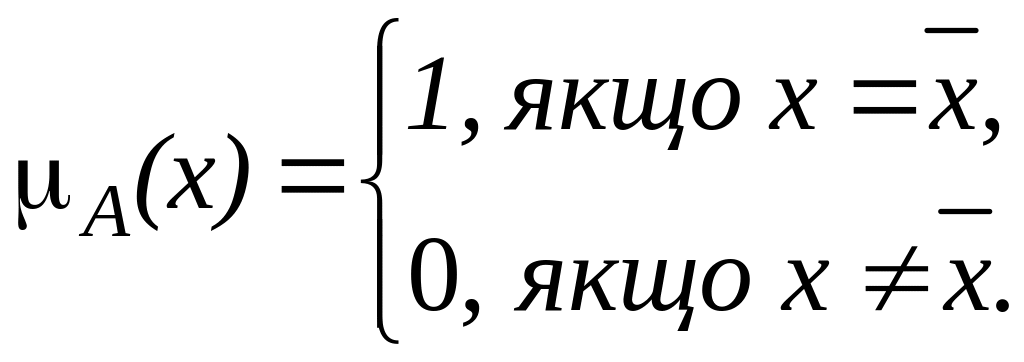
Сінглтон – специфічна функція приналежності, оскільки вона приймає значення 1 лише в єдиній точці простору рішень, яка повністю належить нечіткій множині. В інших точках ця функція приймає значення 0. Така функція приналежності характеризує одноелементну нечітку множину. Єдиним елементом, що повністю належить нечіткій множині , є точка . Функція приналежності типу «сінглтон» використовується переважно для реалізації операції фузифікації, яка застосовується в системах нечіткого виведення.

2. Гаусівська функція приналежності (див. рис. 3.1) визначається виразом:

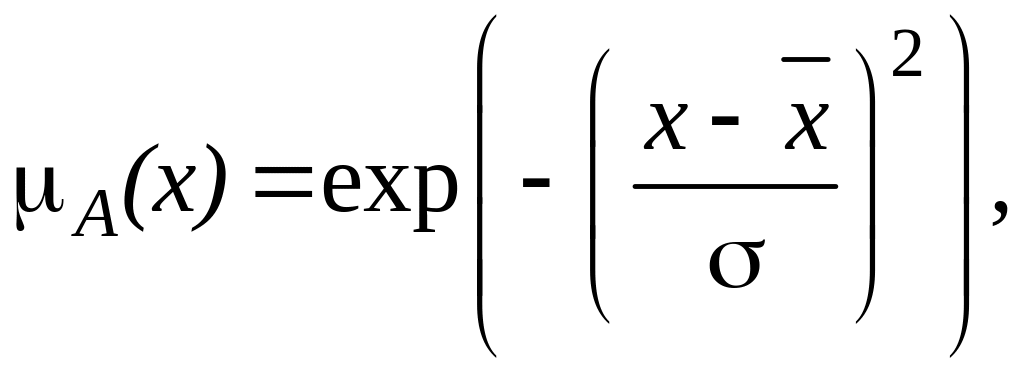
в якому є центром, а визначає ширину гаусівської кривої. Ця функція приналежності зустрічається найчастіше.

Рисунок 3.1 – Графік гаусівської функції приналежності

3. Функція приналежності дзвоноподібного типу (рис. 3.2) задається виразом:

де – відповідно ширина, нахил, центр функції.

Рисунок 3.2 – Графік функції приналежності дзвоноподібного типу

4. Функція приналежності класу (рис. 3.3) визначається у вигляді:

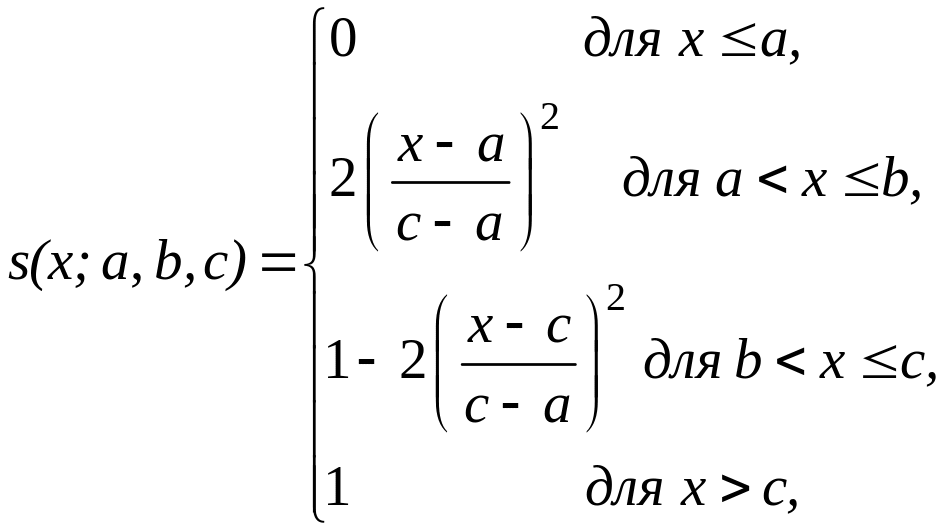
де .

Функція приналежності, що належить до цього класу, має графічне подання (рис. 3.3), що нагадує літеру «s», причому її форма залежить від підбору параметрів , і . У точці функція приналежності класу приймає значення, рівне 0,5.

Рисунок 3.3 – Функція приналежності класу

5. Функція приналежності класу (рис. 3.4) визначається через функцію приналежності класу :

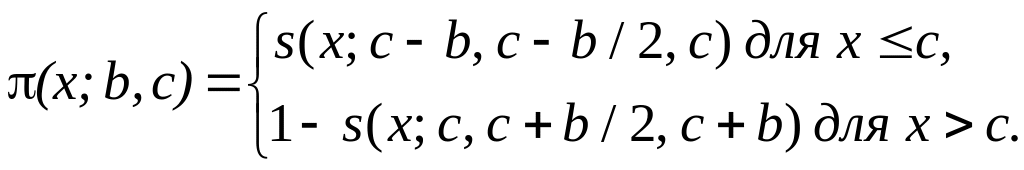
Функція приналежності класу приймає нульові значення для та . У точках її значення дорівнює 0,5.

Рисунок 3.4 – Функція приналежності класу

6. Функція приналежності класу (рис. 3.5) задається виразом:

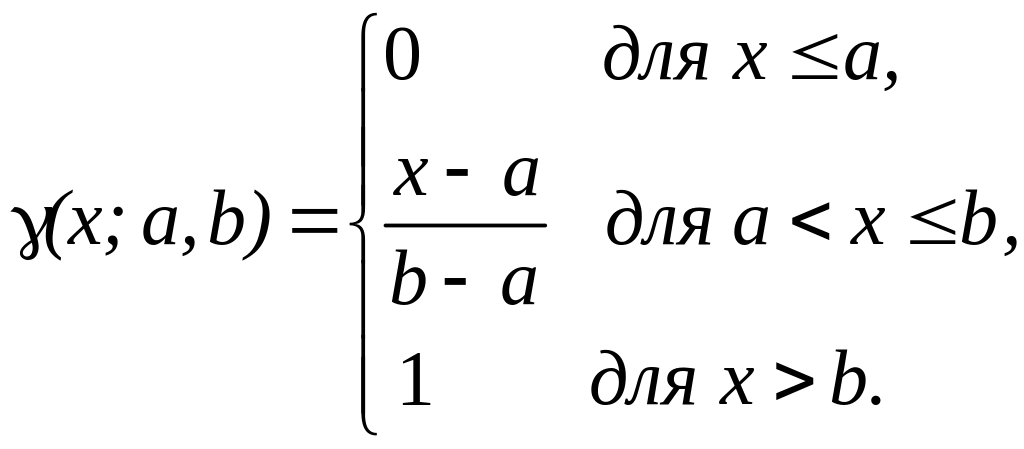
Рисунок 3.5 – Функція приналежності класу

Нескладно помітити аналогію між формами функцій приналежності класів та .

7. Функція приналежності класу (рис. 3.6) визначається у вигляді:

Рисунок 3.6 – Функція приналежності класу

У деяких додатках функція приналежності класу може бути альтернативною відносно функції класу .

8. Функція приналежності класу (рис. 3.7) визначається виразом:

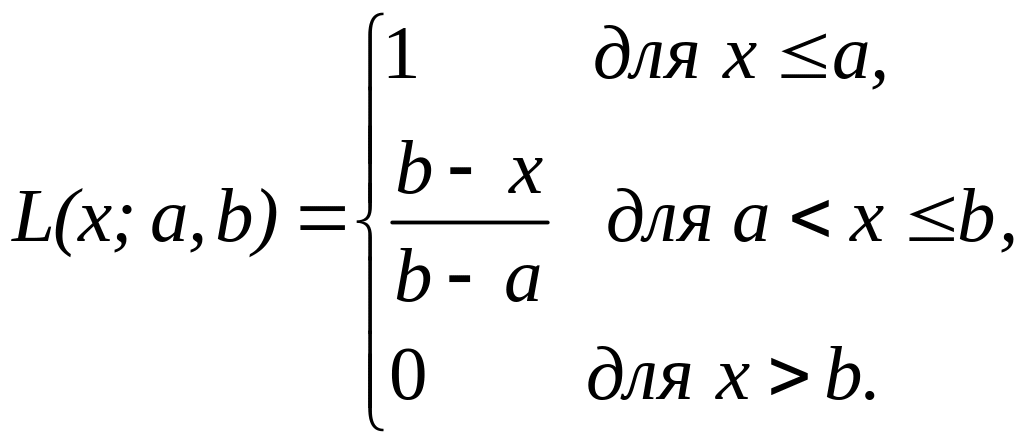
Рисунок 3.7 – Функція приналежності класу

Підставою для побудови функції приналежності можуть бути експертні оцінки.

Виділяють дві групи методів побудови за експертними оцінками функцій приналежності нечіткої множини : прямі та непрямі методи [33].

Прямі методи характеризуються тим, що експерт безпосередньо задає правила визначення значень функції приналежності , яка характеризує елемент . Ці значення узгоджуються з його перевагами на множині елементів так [33, 34]:

1) для будь-яких тоді і тільки тоді, коли переважніше , тобто більшою мірою характеризується властивістю ;

2) для будь-яких тоді і тільки тоді, коли та байдужі щодо властивості .

Як правило, прямі методи задання функції приналежності використовуються для вимірних понять, таких як швидкість, час, тиск, температура тощо.

Різновидами прямих методів є прямі групові методи, коли, наприклад, групі експертів пред'являють конкретний об'єкт, і кожен має дати одну з двох відповідей: чи належить цей об'єкт до заданої множини. Тоді число стверджувальних відповідей, поділене на загальне число експертів, дає значення функції приналежності об'єкта до даної нечіткої множини.

Прямими методами є також безпосереднє задання функції приналежності таблицею, графіком або формулою.

Недоліком цієї групи методів є велика частка суб'єктивізму.

Непрямі методи побудови значень функції приналежності використовуються у випадках, коли немає елементарних вимірних властивостей, через які визначаються нечіткі множини.

У непрямих методах значення функції приналежності вибираються таким чином, щоб задовольнити заздалегідь сформульованим умовам. Експертна інформація є тільки вихідною інформацією для подальшої обробки. До групи даних методів можна віднести такі методики побудови функцій приналежності, як побудова функцій приналежності на основі парних порівнянь, з використанням статистичних даних, на основі рангових оцінок тощо.

Наприклад, метод побудови функції приналежності на основі парних порівнянь заснований на обробці матриць оцінок, що відображають думку експерта про відносну приналежність елементів множині або ступінь вираженості у них властивості, що формалізується множиною [33].

Ступінь приналежності елементів множині визначається за допомогою парних порівнянь. Для порівняння елементів використовуються оцінки, наведені в табл. 3.3.

Розглянутий метод може використовуватися як для вирішення задач вироблення альтернатив, так і для їх порівняння та вибору кращої з них.

Таблиця 3.3 – Шкала для визначення матриці судження

Оцінка важливості	Якісна оцінка	Примітка
1	Однакова значимість	За даним критерієм альтернативи мають однаковий ранг
3	Слабка перевага	Міркування про перевагу однієї альтернативи перед іншою малопереконливі
5	Сильна (або істотна) перевага	Є надійні докази істотної переваги однієї альтернативи
7	Очевидна перевага	Існують переконливі свідчення на користь однієї альтернативи
9	Абсолютна перевага	Свідоцтво на користь переваги однієї альтернативи перед іншою вищею мірою переконливе
2, 4, 6, 8	Проміжні значення між сусідніми оцінками	Використовуються, коли необхідний компроміс

Під час вибору методу побудови функцій приналежності для формалізації медико-біологічних задач необхідно враховувати вид розв'язуваної задачі, складність отримання експертної інформації для її вирішення, достовірність експертної інформації, а також трудомісткість алгоритму обробки інформації під час побудови функції приналежності.

Розглянемо приклад, що ілюструє застосування стандартних функцій приналежності.

Нехай є три неточні формулювання:

- «низька вартість лікарського засобу»;

- «середня вартість лікарського засобу»;

- «висока вартість лікарського засобу».

Як область міркувань = [100, 200].

На рис. 3.8 подані нечіткі множини , і , що відповідають наведеним висловлюванням. Звернемо увагу, що функція приналежності множини має тип , множини – тип , а множини – тип . У фіксованій точці функція приналежності нечіткої множини «низька ціна лікарського засобу» приймає значення 0, тоді як ; .

Рисунок 3.8 – Функції приналежності нечітких множин «низька ціна лікарського засобу», «середня ціна лікарського засобу», «висока ціна лікарського засобу»

3.1.4.2 Основні операції на нечітких множинах

Для нечітких множин застосовні всі властивості та операції, які використовуються для звичайних множин.

Так, нечіткі множини і дорівнюють одна одній, якщо дорівнюють їх функції приналежності і , тобто:

, якщо .

Нечітка множина включає в себе нечітку множину , тобто:

, якщо .

Об'єднанням двох нечітких множин і , заданих на загальній базовій множині , називають найменшу нечітку множину , яка містить водночас як  , так і та має вигляд:

(3.5)

де

Символи і означають «дорівнює за визначенням».

Перетин двох нечітких множин і , заданих на загальній базовій множині , називають найбільшою нечіткою множиною , яка міститься водночас і в , і в та має вигляд

(3.6)

де

Доповненням нечіткої множини , заданої на базовій множині , називають нечітку множину виду:

(3.7)

де

Поняття об'єднання та перетину, які введені для випадку двох вихідних множин і , можуть бути поширені і на випадок декількох вихідних множин.

На рис. 3.9 наведено графічне подання операцій об'єднання, перетину і доповнення нечітких множин (3.5), (3.6), (3.7) [35].

_l(х)

_l(х)

_В 1 _А _С

_В 1 _А _С

_А  _B  _C

_А  _B  _C

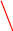
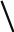
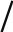
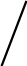
-2 -1 0 1 2 х

-2 -1 0 1 2 х

_j(х)

а) б)

1

_А

 _А

0.5

-2 -1 0 1 2 х

в)

Рисунок 3.9 – Основні операції на нечітких множинах

Операції алгебри логіки (див. табл. А.1) застосовні і до нечітких висловлювань, що використовуються в нечіткій логіці, якщо кожний вислів, наприклад , характеризувати функцією істинності (ФІ) – , аналогічної в певному сенсі функції приналежності.

Тоді можуть бути введені такі аналоги звичайних логічних операцій:

- нечітке заперечення:

(3.8)

- нечітка диз'юнкція:

(3.9)

- нечітка кон'юнкція:

(3.10)

- нечітка імплікація:

(3.11)

Неважко переконатися, що нечіткі логічні операції (3.8) – (3.11) за окремих значень ФІ і , рівних 1 і 0, повністю порядковуються правилам алгебри логіки, наведеним у табл. А.1.

З формул (3.8) – (3.11) можна зробити такі висновки щодо істинності різних висловлювань (логічних операцій):

- ступінь істинності заперечення якого-небудь висловлювання (операції "НЕ") дорівнює ступеню хибності вихідного висловлювання;

- ступінь істинності диз'юнкції двох висловлювань (операції «АБО») збігається зі ступенем істинності більш істинного висловлювання;

- ступінь істинності кон'юнкції двох висловлювань (операції "І") збігається зі ступенем істинності менш істинного висловлювання;

- ступінь істинності імплікації (висловлювання «ЯКЩО ..., ТО») тим більше, чим менше ступінь істинності посилання і чим більше ступінь істинності висновку; якщо у висновку ступінь істинності більше, ніж у посилання, то ступінь істинності імплікації дорівнює одиниці.

Зазначимо, що замість операцій бінарної логіки «АБО», «І», наведених у табл. А.1, і операцій нечіткої логіки (3.9), (3.10) можна застосовувати їх арифметичні аналоги:

де – функції істинності, що приймають тільки значення 1 або 0, або ж функції приналежності, які приймають будь-які значення в інтервалі [0,1].

Розглянемо приклад використання нечіткої логіки для формалізації нечіткого висловлювання: «Біоінженери, що володіють технічними знаннями І медичними, мають добрі професійні перспективи у галузі медичної інформатики АБО медичного приладобудування». Нехай окремі частини цього висловлювання характеризуються такими значеннями:

: інженери володіють технічними знаннями – ;

: інженери володіють знаннями медичними – ;

: є добрі перспективи для діяльності біоінженера – ;

: є добрі перспективи для роботи IT-фахівцем в медицині – .

Повний вислів можна подати у вигляді імплікації:

у якій функція істинності, відповідно до формул (3.10), (3.9) і (3.11), дорівнює:

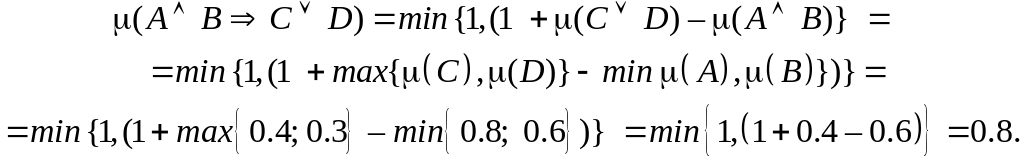
З наведеного прикладу і формули (3.11) випливає така загальна властивість:

якщо

тобто істинне значення імплікації (логічного висновку) дорівнює одиниці, якщо істинне значення посилання не більше істинного значення висновку.

3.1.4.3 Нечітка та лінгвістична змінні

Для опису нечітких множин вводяться поняття нечіткої та лінгвістичної змінних.

Нечітка змінна описується набором , де – це назва змінної, – універсальна множина (область міркувань), – нечітка множина на .

Лінгвістична змінна – це змінна, значення якої визначається набором вербальних (тобто словесних) характеристик деякої властивості, тобто лінгвістична змінна – це змінна, значеннями якої є не числа, а слова або речення на природній або формальній мові.

Використання слів і пропозицій, а не чисел, мотивоване тим, що лінгвістичний опис, як правило, менш конкретний, ніж опис числами. Наприклад, фраза «Пацієнт молодий» менш конкретна, ніж фраза «Пацієнту 25 років». У цьому сенсі слово молодий можна розглядати як лінгвістичне значення змінної «Вік», маючи на увазі при цьому, що лінгвістичне значення відіграє таку саму роль, як і чисельне значення 25, але є менш точним і, отже, менш інформативним. Те саме можна сказати про лінгвістичні значення «дуже молодий», «не молодий», «надзвичайно молодий», «не дуже молодий» тощо, якщо їх зіставити з чисельними значеннями 20, 21, 22, 23 [36].

Сукупність значень лінгвістичної змінної становить терм-множина цієї змінної. Ця множина може мати нескінченне число елементів. Наприклад, терм-множину лінгвістичної змінної «Вік» можна записати так:

Т (Вік) = молодий + не молодий + дуже молодий + не дуже молодий + дуже-дуже молодий + старий + не старий + дуже старий + не дуже старий + не дуже молодий і не дуже старий + середнього віку + не середнього віку + не старий і не середнього віку + надзвичайно старий.

Знак «+» позначає тут об'єднання, а не арифметичне підсумовування. Аналогічно, терм-множину лінгвістичної змінної «Зовнішність» можна записати так:

Т (Зовнішність) = прекрасна + гарненька + миловидна + красива + приваблива + не прекрасна + дуже гарненька + дуже дуже красива + більш-менш гарненька + досить гарненька + досить красива + безумовно красива + не дуже приваблива, але і не дуже неприваблива.

У разі лінгвістичної змінної числова змінна «Вік», приймаюча значення 0, 1, 2, 3, ..., 100, є так званою базовою змінною лінгвістичної змінної «Вік». При цьому таке, наприклад, лінгвістичне значення, як молодий, можна інтерпретувати як назву деякого нечіткого обмеження на значення базової змінної. Саме це обмеження ми і вважаємо змістом лінгвістичного значення «молодий».

Звичайна інтерпретація висловлювання «Пацієнт молодий» полягає в тому, що «Пацієнт» належить до класу молодих людей. Однак, беручи до уваги, те, що клас молодих людей – нечітка множина, тобто що не існує різкого переходу від молодості до «не молодості», твердження про те, що «Пацієнт» належить до класу молодих людей, не відповідає точному математичному визначенню поняття «належить». Концепція лінгвістичної змінної дозволяє обійти цю трудність так.

«Пацієнт» розглядається як назва складової лінгвістичної змінної, компонентами якої є лінгвістичні змінні «Вік», «Зріст», «Вага», «Зовнішність» тощо. Тоді вислів «Пацієнт молодий» інтерпретується як: «Вік = молодий», тобто приписується значення «молодий» лінгвістичній змінній «Вік». У свою чергу значення «молодий» інтерпретується як назва деякого нечіткого обмеження на базову змінну «Вік».

На рис. 3.10 подана формалізація неточного поняття "Вік людини". Так, для людини 48 років ступінь приналежності до множини «Молодий» дорівнює 0 «Середній» – 0.47, «Вище середнього» – 0.20.

Рисунок 3.10 – Опис лінгвістичної змінної «Вік»

Чим більше вік людини, тим менше стає ії приналежність до молодих, тобто ранг прагнутиме до 0 (рис. 3.11):

- до 16 років не можна однозначно стверджувати, що людина молода (рангом близько 0,9);

- від 16 до 30 років можна сміливо присвоїти ранг 1, тобто людина в цьому віці молода;

- після 30 років людина начебто вже не молода, але ще й не стара, тут ранг прийматиме значення в інтервалі від 0 до 1.

Рисунок 3.11 – Зміна рангу в залежності від віку людини

Значеннями лінгвістичної змінної можуть бути нечіткі змінні, тобто лінгвістична змінна знаходиться на більш високому рівні, ніж нечітка змінна. Кожна лінгвістична змінна складається з:

- назви ;

- множини своїх значень, яка також називається базовою терм-множиною . Елементи базової терм-множини являють собою назви нечітких змінних;

- універсальної множини ;

- синтаксичного правила , за яким генеруються нові терми із застосуванням слів природної або формальної мови;

- семантичного правила , яке кожному значенню лінгвістичної змінної ставить у відповідність нечітку підмножину множини .

Приклад. Нехай експерт оцінює товщину стінки лівого шлуночка серця за допомогою понять: «мала товщина», «середня товщина», «велика товщина»; при цьому мінімальна товщина дорівнює 0.3 см, а максимальна – 5 см.

Формалізація такого опису може бути проведена за допомогою лінгвістичної змінної: , де – «товщина стінки»; .

Нехай нечіткі множини описують семантику базових значень змінної . Функції приналежності наведені на рис. 3.12.

Рисунок 3.12 – Функції приналежності нечітких множин

Тоді значення «мала або середня товщина», визначається нечіткою множиною , функція приналежності якої подана на рис. 3.13, а значення «невелика товщина» визначатиметься нечіткою множиною , функція приналежності якої подана на рис. 3.14.

Рисунок 3.13 – Функція приналежності нечіткої множини

Рисунок 3.14 – Функція приналежності нечіткої множини

3.1.4.4 Нечіткі відносини

Одним з основних понять теорії нечітких множин вважається поняття нечіткого відношення. Ці відношення дозволяють формалізувати неточні твердження типу « майже дорівнює » або « значно більше ніж ». Наведемо визначення нечіткого відношення [37].

Нечітким відношенням між двома не порожніми (чіткими) множинами і називатимемо нечітку множину, яка визначена на декартовому добутку , тобто:

Іншими словами, нечітке відношення – це множина пар:

_де є функцією приналежності, яка кожній парі приписує її ступінь приналежності , що інтерпретується як сила зв'язку між елементами и .

Нечітке відношення можна подати у вигляді:

_або

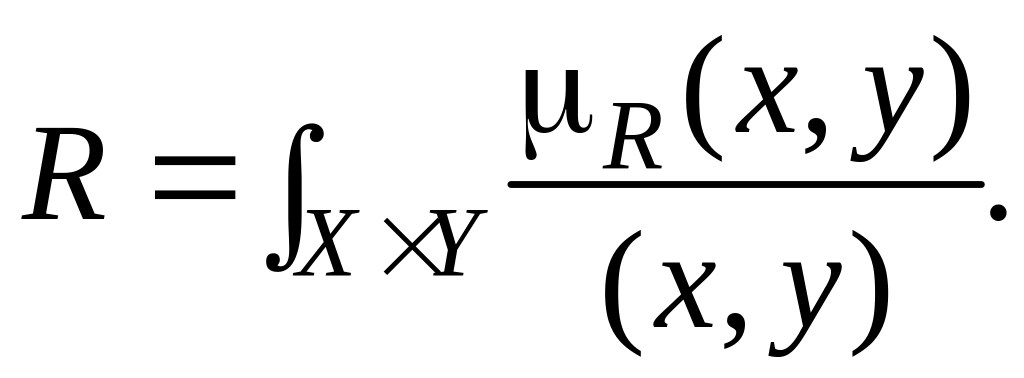
Приклад 1. Застосуємо визначення нечіткого відношення для формалізації неточного затвердження « приблизно дорівнює ». Нехай и . Відношення можна визначити так:

Отже, функція приналежності відношення має вигляд:

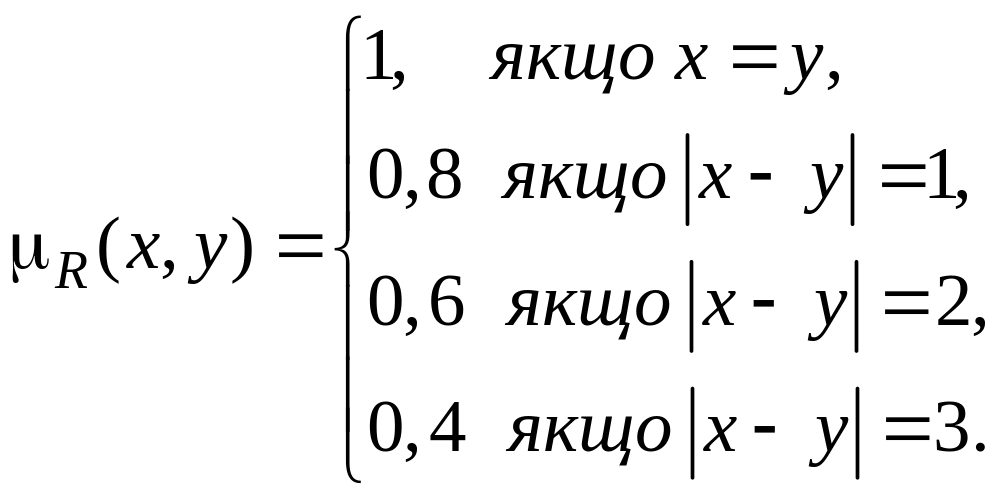
Відношення також можна задати у вигляді матриці:

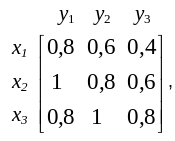
де

Приклад 2. Нехай – тривалість життя людини. У цьому випадку відношення з функцією приналежності:

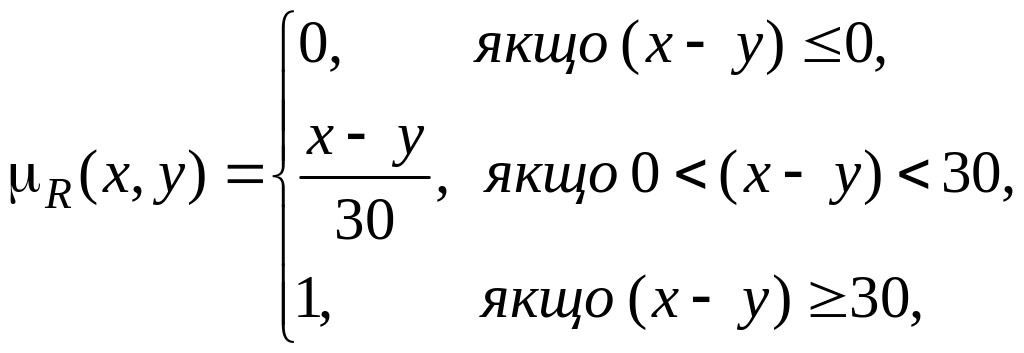
являє неточне твердження «особа у віці набагато старше особи у віці ».

Слід підкреслити, що нечітке відношення – нечітка множина, тому зберігають силу визначення операцій перетину, підсумовування та доповнення:

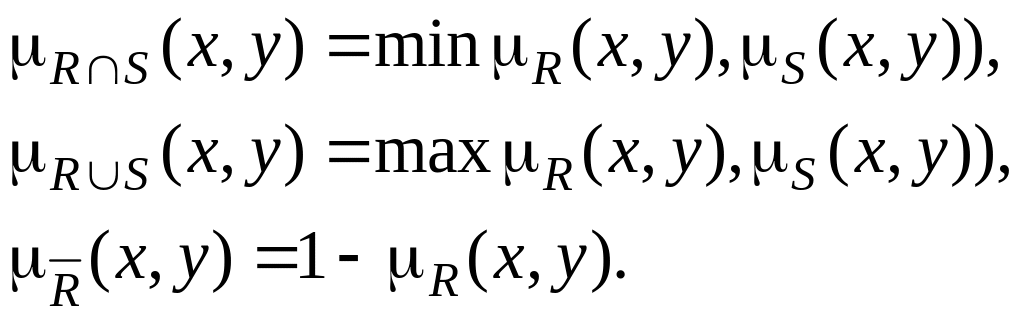
3.1.4.5 Нечітке логічне виведення

Системи нечіткого виведення призначені для реалізації процесу нечіткого виведення і є базисом всієї сучасної нечіткої логіки. Системи нечіткого виведення дозволяють вирішувати задачі автоматичного управління, класифікації даних, розпізнавання образів, прийняття рішень, машинного навчання та багато інших.

Алгоритми нечіткого виведення розрізняються переважно видом використовуваних правил, логічних операцій і різновидом методу дефузифікації. Розроблено моделі нечіткого виведення Мамдані, Сугено, Ларсена, Цукамото.

Основними компонентами системи нечіткого виведення (див. рис. 3.15) є:

- база правил;

- блок фузифікаціії;

- блок вироблення рішення (блок виведення);

- блок дефузифікації.

Рисунок 3.15 – Система нечіткого логічного виведення [37]

Основою для проведення операції нечіткого логічного виведення є база правил, яка містить нечіткі висловлювання у формі «Якщо – то» і функції приналежності для відповідних лінгвістичних термів. При цьому мають дотримуватися такі умови:

1) існує хоча б одне правило для кожного лінгвістичного терма вихідної змінної;

2) для будь-якого терма вхідної змінної є хоча б одне правило, в якому цей терм використовується як передумова (ліва частина правила).

В іншому випадку має місце неповна база нечітких правил.

Система управління з нечіткою логікою оперує нечіткими множинами. Тому конкретне значення _{вхідного сигналу модуля нечіткого управління підлягає операції фузифікації (англ. fuzzi fication), внаслідок якої йому буде зіставлена нечітка множина .} Тобто під фузифікацією розуміється не тільки окремий етап виконання нечіткого виведення, але й власне процес знаходження значень функцій приналежності нечітких множин, тобто це просто введення нечіткості. У завданнях управління найчастіше застосовується операція фузифікації типу «сінглтон»:

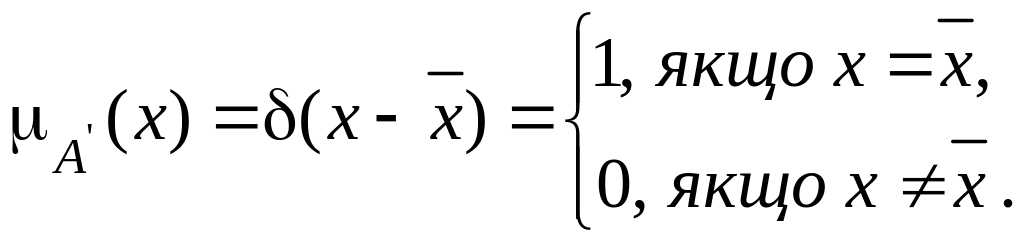
Нечітка множина подається на вхід блока вироблення рішення. Якщо вхідний сигнал надходить з шумами, то нечітку множину можна визначити функцією приналежності:

_де

У блоці вироблення рішення усі нечіткі множини, які призначені для кожного терму кожної вихідної лінгвістичної змінної, поєднуються разом, і формується єдина нечітка множина – значення для кожної виведеної лінгвістичної змінної.

Припустимо, що на вхід блока вироблення рішення (блок виведення) подана нечітка множина . На виході блока вироблення рішення відповідно до узагальненого нечіткого правила modus ponens отримуємо нечітких множин .

На виході блока вироблення рішення формується або нечітких множин з функціями приналежності , або одна нечітка множина з функцією приналежності . Постає задача відображення нечітких множин (або нечіткої множини в єдине значення , яке являє собою керуючий вплив, що подається на вхід об'єкта. Таке відображення називається дефузифікацією (приведення до чіткості), воно реалізується в однойменному блоці.

Якщо на виході блока вироблення рішення формується нечітких множин , то значення можна розрахувати за допомогою різних методів.

Розглянемо метод дефузифікації за середнім центром (англ. center average defuzzification). Значення розраховується по формулі:

де – точка, в якій функція приймає максимальне значення, тобто:

Точка називається центром (англ. center) нечіткої множини . На рис. 3.16 подана ідея цього методу для . Звернемо увагу, що значення не залежить від форми та носія функції приналежності .

Рисунок 3.16 – Ілюстрація методу дефузифікації за середнім центром

Розглянемо принцип побудови алгоритму нечіткого виведення на конкретному прикладі.

Лінгвістична змінна «рівень артеріального тиску (АТ)» може мати такі терми: «підвищувати швидко», «підвищувати повільно», «не змінювати», «знижувати повільно», «знижувати швидко». Кожен терм описується своєю функцією приналежності , яка може приймати значення від 0 до 1. Отримавши чисельне значення вхідної змінної у блоці фузифікації, обчислюється значення кожного терма. Результатом застосування правила є величина, звана ступенем істинності, тобто число від 0 до 1. Так, нехай є рівень АТ який змінюється залежно від стану пацієнта і просте правило: якщо стан пацієнта «колаптоїдний», то АТ «підвищувати швидко». У нас є вхідна величина рівень у мм. рт. ст. Якщо величина рівня АТ очевидно низька »( , де – функція приналежності для трема «низький»), або рівень очевидно високий (( ), то все відбувається як і у звичайній логіці, ступінь істинності правила приймає значення 1 або 0. Нечіткість починається, якщо , наприклад . Рівень низький, але не дуже. Відповідно змінювати рівень артеріального тиску за допомогою лікарських засобів потрібно швидко, але не дуже. В даному правилі ступінь істинності дорівнює 0.5. Подібним чином відбувається її обчислення для кожного правила. У блоці вироблення рішення висновки з кожного правила об'єднуються разом для кожної лінгвістичної змінної. Наприклад, після визначення набору правил ми отримуємо результати для лінгвістичної змінної рівень АТ: «підвищувати швидко» – 0.5, «підвищувати повільно» – 0.3, «не змінювати» – 0, «знижувати повільно» – 0, «знижувати швидко» – 0 . Зрозуміло, що зміна рівня АТ лежить десь між повільно і швидко. Знаючи ступінь істинності для кожного терма вихідної змінної, можна розрахувати її числове значення. Що і відбувається у блоці дефузифікації.

Таким чином, ми розглянули основні аспекти формалізації медичних знань.

Під час вирішення медико-біологічних задач на комп'ютері виконуються декілька найбільш важливих послідовних етапів, першим з яких є саме формалізація. Потім проводяться алгоритмізація, програмування, оцінка та аналіз отриманих результатів.

Рішення будь-якої інженерної задачі, заснованої на законах та рівняннях хімії, біохімії, біофізики показує, що найбільш складною і трудомісткою частиною є етап формалізації завдання, що вимагає високого рівня кваліфікації дослідника.

Практика показує, що адекватна формалізація досить складних завдань вимагає порядку 70% часових витрат для реалізації завдання на комп'ютері.

Наступним важливим етапом є алгоритмізація.

Під алгоритмізацією розуміють процес побудови алгоритму розв'язання задачі, результатом якого є виділення етапів процесу обробки та аналізу даних, формальний запис змісту цих етапів і визначення порядку їх виконання [38].

3.2 Основи алгоритмізації медичних задач

Сучасні інформаційні системи дозволяють зберігати і за лічені секунди обробляти дані практично будь-якого обсягу. Алгоритмізація з подальшою комп'ютеризацією аналізу накопиченої медичної інформації лежить в основі розробки та створення МІС.

3.2.1 Основні властивості алгоритмів і методи їх опису

У IX ст. видатний математик середньовічного сходу Мухаммед аль-Хорезмі у своїй книзі "Про індійський рахунок" сформулював правила запису натуральних чисел за допомогою арабських цифр і правила дій над ними стовпчиком. В подальшому алгоритмом стали називати «точний припис», який визначає послідовність дій, що забезпечує отримання необхідного результату з вихідних даних. У XII ст. був виконаний латинський переклад його математичного трактату, з якого європейці дізналися про десяткову позиційну систему числення і правила арифметики багатозначних чисел. Саме ці правила в той час називали алгоритмами (algorithmi – від латинського написання імені аль-Хорезмі). Потім словом "алгоритм" стали позначати сукупність правил певного виду, а не тільки правила виконання арифметичних дій.

Алгоритм – це впорядкований кінцевий набір чітко визначених правил для вирішення задач за кінцеву кількість кроків.

Говорячи про алгоритми, необхідно розглянути джерела їх виникнення.

Перше джерело – це практика, наше повсякденне життя, що дає можливість, а іноді й вимагає отримувати алгоритми шляхом опису дій за рішенням різних задач. Такі алгоритми називаються емпіричними.

Друге джерело – це наука. З її теоретичних положень і встановлених фактів можуть бути виведені алгоритми. Так, на основі теоретичних законів можна побудувати алгоритми для управління різними технологічними процесами.

Третім джерелом є різні комбінації та модифікації вже наявних алгоритмів. Прикладами алгоритмів є правила приготування ліків в аптеці, інструкції прийняття ліків, процес лікування хворого тощо.

Будь-який алгоритм повинен мати такі основні властивості [39]:

- визначеність. Алгоритм не повинен включати вказівки, зміст яких може бути сприйнято неоднозначно. Крім того, після виконання чергової вказівки алгоритму не повинно виникати жодних протиріч відносно того, яка вказівка виконуватиметься наступною. Інакше кажучи, під час виконання алгоритму ніколи не повинна з'являтися потреба у прийнятті будь-яких непередбачених рішень укладача алгоритму;

- однозначність – за одних і тих самих початкових даних результат виконання алгоритму призводить до одного і того самого результату;

- масовість. Алгоритм розробляється не для вирішення однієї конкретної задачі, а для цілого класу задач одного типу. У найпростішому випадку ця варіативність алгоритму забезпечує можливість використання різних допустимих початкових даних;

- дискретність. Процес, який описується алгоритмом, має бути розділений на послідовність окремих дій. Опис, який при цьому виникає, являє собою послідовність чітко відокремлених одна від одної вказівок, які утворюють дискретну структуру алгоритмічного процесу – тільки виконавши вимоги однієї вказівки, можна перейти до наступної;

- результативність – обов'язкова властивість алгоритмів. Ії суть полягає в тому, що при точному виконанні всіх вказівок алгоритму процес ухвалення рішення (одержання результату) має закінчитися через кінцеве число кроків і при цьому має бути отримана відповідь на поставлені у задачі питання;

- зрозумілість – алгоритм має бути зрозумілий для виконавця;

- ефективність – з можливих алгоритмів вибирається той, який містить менше кроків, або часу на його виконання потрібно менше.

Вибір засобів і методів для запису алгоритму залежить, насамперед, від призначення самого алгоритму, а також від того, хто його розроблятиме.

Як виконавця алгоритму можна розглядати людину і технічні пристрої, серед яких особливе місце займає комп'ютер.

Існує декілька методів опису алгоритмів:

- природною мовою (словесний спосіб) з ретельним добіром слів і фраз, що не допускають зайвих слів, двозначностей і повторень, доповнюється мова звичайними позначеннями та деякими спеціальними угодами;

- за допомогою формул, рисунків, таблиць. Під час подання алгоритму за допомогою загальноприйнятих графічних фігур (наприклад, блоків), кожна з них описує один або декілька кроків алгоритму. Усередині блока записується опис команд або умов. Для вказівки послідовності виконання блоків використовують лінії зв'язку (лінії з'єднання). Послідовність блоків і ліній утворюють схему алгоритму;

- спеціальною (формальною) мовою.

Під час складання структурної схеми алгоритму укладач має дотримуватися таких правил:

1) будь-який алгоритм повинен мати початок і кінець;

2) усі блоки, крім перевірки умови, мають тільки один вихід;

3) усі блоки алгоритму мають не більше одного входу;

4) лінії алгоритму можуть розгалужуватися.

Найбільш часто вживані графічні символи (повний список включає 42 символи) наведені у табл. А.2.

Розміри символів. Розмір a має обиратися з ряду 10, 15, 20 мм. Допускається збільшувати розмір на число, кратне 5. Розмір дорівнює . Під час ручного виконання схем алгоритмів і програм для розглянутих символів 1-6, 13 допускається встановлювати рівним . Під час виконання умовних графічних позначень автоматизованим способом розміри геометричних елементів символів округляються до значень, що визначаються технічними можливостями використовуваних пристроїв [40].

3.2.2 Методи розробки та аналізу алгоритмів

Розглянемо основні методи проектування (низхідний, висхідний, модульний, структурний) алгоритмів.

Низхідним проектуванням алгоритмів, проектуванням алгоритмів «зверху вниз» або методом послідовної (покрокової) низхідної розробки алгоритмів називається такий метод складання алгоритмів, коли вихідна задача (алгоритм) розбивається на ряд допоміжних підзадач (підалгоритмів), що формулюються і вирішуються в термінах більш простих та елементарних операцій (процедур). Останні, в свою чергу, знову розбиваються на більш прості й елементарні, і так до тих пір, поки не дійдемо до команд виконавця. У термінах цих команд можна подати та виконати отримані на останньому кроці розбиття, підалгоритми (команд, системи команд виконавця) [41].

За допомогою висхідного методу, навпаки, спираючись на деякий, заздалегідь обумовлений коректний набір підалгоритмів, будують функціонально завершені підзадачі більш загального призначення, від них переходять до більш загальних, і так далі, до тих пір, поки не дійдемо до рівня, на якому можна записати вирішення поставленої задачі. Цей метод відомий як метод проектування «знизу вверх».

Структурні принципи алгоритмізації (структурні методи алгоритмізації) – це принципи формування алгоритмів з базових структурних алгоритмічних одиниць (слідування, розгалуження, повторення), використовуючи їх послідовне з'єднання або вкладення один в одного з дотриманням певних правил, що гарантують читабельність і виконуваність алгоритму зверху вниз і послідовно.

Структурований алгоритм – це алгоритм, поданий як слідування і вкладення базових алгоритмічних структур. У структурованого алгоритму статичний стан (до актуалізації алгоритму) і динамічний стан (після актуалізації) мають однакову логічну структуру, яка простежується зверху вниз ("як читається, так і виконується"). Під час структурованої розробки алгоритмів правильність алгоритму можна простежити на кожному етапі його побудови та виконання.

Згідно з теоремою (про структурування) будь-який алгоритм може бути еквівалентно поданий структурованим алгоритмом, що складається з базових алгоритмічних структур [41].

Одним з широко використовуваних методів проектування та розробки алгоритмів (програм) є модульний метод (модульна технологія).

Модуль – це певний алгоритм або певний його блок, що має конкретне найменування, за яким його можна виділити й актуалізувати. Іноді модуль називається допоміжним алгоритмом, хоча всі алгоритми носять допоміжний характер. Ця назва має сенс, коли розглядається динамічний стан алгоритму; у цьому випадку можна назвати допоміжним будь-який алгоритм, використовуваний як блок (складова частина) тіла цього динамічного алгоритму. Використовують й іншу назву модуля – підалгоритм. У програмуванні використовуються синоніми – процедура, підпрограма.

Властивості модулів:

- функціональна цілісність і завершеність (кожен модуль реалізує одну функцію, але реалізує добре й повністю);

- автономність і незалежність від інших модулів (незалежність роботи модуля-наступника від роботи модуля-попередника; при цьому їх зв'язок здійснюється лише на рівні передачі/прийому параметрів та управління);

- еволюція (розвиток);

- відкритість для користувачів і розробників (для модернізації та використання);

- коректність і надійність;

- посилання на тіло модуля відбувається тільки за іменем модуля, тобто виклик і актуалізація модуля можливі тільки через його заголовок.

Властивості (переваги) модульного проектування алгоритмів:

- можливість розробки алгоритму великого обсягу (алгоритмічного комплексу) різними виконавцями;

- можливість створення та ведення бібліотеки найбільш часто використовуваних алгоритмів (підалгоритмів);

- полегшення тестування алгоритмів і обґрунтування їх правильності;

- спрощення проектування та модифікації алгоритмів;

- зменшення складності розробки (проектування) алгоритмів (або комплексів алгоритмів);

- спостереження обчислювального процесу під час реалізації алгоритмів.

Тестування алгоритму – це перевірка правильності чи неправильності роботи алгоритму на спеціально заданих тестах або тестових прикладах – задачах з відомими вхідними даними і результатами. Тестовий набір має бути мінімальним і повним, тобто має забезпечувати перевірку кожного окремого типу наборів вхідних даних, особливо виняткових випадків.

Тестування алгоритму не може дати повної (100%-ї) гарантії правильності алгоритму для всіх можливих наборів вхідних даних, особливо для достатньо складних алгоритмів. Для нескладних алгоритмів грамотний підбір тестів і повне тестування може дати повну картину працездатності (непрацездатності).

Повну гарантію правильності алгоритму може дати опис роботи і результатів алгоритму за допомогою системи аксіом і правил виведення або верифікація алгоритму.

Трасування – це метод покрокової фіксації динамічного стану алгоритму на деякому тесті. Часто здійснюється за допомогою трасувань таблиць, у яких кожен рядок відповідає певному стану алгоритму, а стовпчик – певному стану параметрів алгоритму (вхідних, вихідних і проміжних). Трасування полегшує налагодження та розуміння алгоритму.

Процес пошуку і виправлення (явних чи неявних) помилок в алгоритмі називається налагодженням алгоритму.

Деякі (приховані та ті, що важко виявляються) помилки у складних програмних комплексах можуть виявитися тільки в процесі їх експлуатації, на останньому етапі пошуку та виправлення помилок – етапі супроводу. На цьому етапі також уточнюють і покращують документацію, навчають персонал використанню алгоритму (програми).

3.2.3 Діагностичні алгоритми

Без точного діагнозу неможливе правильне лікування. Ця аксіома пояснює важливість швидкої і точної діагностики в медицині. Часто медична діагностика являє собою область різноманітних задач професійного вироблення рішень у складних ситуаціях або ситуаціях з неповною інформацією. Особливість роботи лікаря полягає в тому, що об'єкт (хворий) надзвичайно складний, а рішення має бути ухвалене обов'язково. Значна частина інформації про хворого має невербальний характер. Формалізація та структуризація хоча б частини використовуваної лікарем інформації може бути корисна для самого лікаря (частина питань спроститься і може бути вирішена формально, це звільняє свідомість для вирішення більш складних професійних проблем). Крім того, полегшиться передача його досвіду новому поколінню фахівців. У медицині розробляються алгоритми стандартизованих дій під час обробки матеріалів досліджень, постановки діагнозу тощо.

Діагностичний алгоритм – набір формальних правил, що дозволяє на основі відомостей про хворого сформулювати діагноз захворювання. Алгоритмізація прискорює діагностику, але не виключає повністю перебору симптомів і діагнозів. Іншими словами, алгоритмізований діагноз заснований на ітеративному діагнозі, випливає з нього, але повна й вичерпна ітерація симптомів та варіантів діагностичних висновків буває при цьому не потрібна. І в цьому перевага алгоритмізованого діагнозу. Він дозволяє більшою мірою механізувати діагностичну роботу лікаря.

Діагностичний алгоритм складається як для безпосереднього використання медпрацівниками, так і для вирішення діагностичних задач за допомогою ЕОМ.

Існує декілька форм запису діагностичного алгоритму. Розглянемо найбільш часто використовувані в медицині: за допомогою слів, формул, диференційно-діагностичних таблиць, таблиць рішень, графічних схем.

Графічний спосіб подання алгоритмів є більш компактним і наочним порівняно зі словесним. Для прикладу наводиться графічний варіант діагностичного алгоритму для синдрому обширного затемнення легеневого поля (див. схему в додатку Б).

Графічне зображення алгоритму гіпотензивної терапії глаукоми наведено на рис. 3.17.

Класифікаційні дерева також являють собою графічний спосіб опису діагностичного алгоритму.

Рисунок 3.17 – Алгоритм гіпотензивної терапії глаукоми. Схема призначень для досягнення внутрішньоочного тиску (ВОТ) за «метою»

Класифікаційні дерева – це дерева, що відображають ту чи іншу класифікацію, загальноприйняту в даній предметній області. На рис. 3.18 наведено приклад класифікації хвороб нирок.

Рисунок 3.18 – Приклад класифікації хвороб нирок

Таблиці рішень (decision table) являють собою таблиці, в яких вказані дії, що вживаються в різних умовах, причому рішення – це вибір між альтернативними діями. Зазвичай таблиця складається з чотирьох частин, розташування і призначення яких показано в табл. 3.4.

Таблиця 3.4 – Таблиця рішень

Попередні умови	Остаточні умови
Можливі дії	Здійснювані дії

У розділі «Попередні умови» перераховані окремі умови, від яких залежать їхні дії, а в розділі «Можливі дії» – дії, які можуть бути зроблені. У розділі «Остаточні умови» перераховані уточнення передумов, за яких робляться ті чи інші дії. Цей розділ організований у вигляді стовпчиків, у кожному з яких дається уточнення кожної предумови. Потім у стовпчиках розділу «Здійснювані дії» проставляються хрестики, які вказують на вчинення тієї або іншої дії. Зазвичай у таблиці всі можливі комбінації вхідних значень (передумов) перераховані так, що застосування таблиці завжди дає в точності одну здійснювану дію.

Табл. 3.5 являє собою приклад таблиці рішень під час діагностики артеріальної гіпертензії (АГ) у підлітків. Символ «-» у розділі «Остаточні умови» означає «байдуже».

Таблиця 3.5 – Приклад таблиці рішень під час діагностики АГ у підлітків

Головний біль	Так	Так	Ні	Так	Ні	Так	Ні	Ні
Підвищення АТ	Так	Ні	Так	Ні	Ні	Так	Так	Ні
Болі в серці	Ні	Ні	Ні	Так	Так	Так	Так	Ні
Зробити ЕКГ				+	+	+	+
Провести холтерівське моніторування АТ	+		+
Відвідати невролога		+
Не проводити досліджень								+

Диференційна діагностика – це термін у медицині, призначений для позначення способу постанови діагнозу, в якому виключаються невідповідні варіанти. Таким чином, має залишитися один варіант, який і буде діагнозом. Диференціальна діагностика деяких захворювань очей наведена в табл. 3.6.

Таблиця 3.6 – Диференційна діагностика гострого кон'юнктивіту, гострого іридоцикліту, гострого нападу закритокутової глаукоми та ендофтальміту

Клінічна ознака	Гострий кон'юнктивіт	Гострий іридоцикліт	Гострий приступ закритокутової глаукоми	Ендофтальміт
Гострота зору	Не змінена	Не змінена або знижена	Різко знижена	Знижена частково
Біль	Немає	Помірна	Дуже сильна	Слабка
Циліарна болючість	Немає	Виражена	Немає	Немає
Кон'юнктива	Гіперемована	Не змінена	Не змінена	Гіперемована
Виділення з кон'юнктивальної порожнини	Є (слизове або слизово-гнійне)	Немає	Немає	Немає
Ін'єкція очного яблука	Немає	Перікорнеальна	Змішана, застійна	Застійна
Рогівка	Не змінена	Набрякла	Не змінена	Набрякла
Глибина передньої камери	Середньої глибини	Середньої глибини	Дрібна, щілиновидна	Середньої глибини
Райдужка	Не змінена	Набряк, гіперемія, зміна кольору	Можлива секторальна атрофія	Не змінена
Зіниця	Не змінена, реакція на світло збережена	Міоз, зміна форми (задні синехії), реакція на світло ослаблена	Мідріаз, на світло не реагує	Реакції на світло мляві, рефлекс тьмяний або відсутній
Скловидне тіло	Не змінено	Не змінено	Не змінено	Ексудат
Внутрішньоочний тиск	Норма	Норма або гіпотонія (іноді гіпертензія)	Високе	Норма
Зміни загального стану	Немає	Немає	Головний біль, блювання, підвищення артеріального тиску	Немає

Наведемо ще ряд прикладів діагностичних алгоритмів, розроблених для МІС.

Апаратно-програмний комплекс «Кардиолаб» [6] забезпечує реалізацію алгоритму аналізу варіабельності серцевого ритму (ВСР).

ВСР є методом оцінки стану механізмів регуляції фізіологічних функцій в організмі людини, зокрема, загальної активності регуляторних механізмів, нейрогуморальної регуляції серця, співвідношення між симпатичним і парасимпатичним відділами вегетативної нервової системи.

Аналіз ВСР заснований на вимірюванні часових інтервалів між R-зубцями моніторної електрокардіограми ( інтервалів) (рис. 3.19) і подальшої їх оцінки статистичними, геометричними та спектральними методами.

Рисунок 3.19 – Запис моніторної електрокардіограми з визначенням тривалостей -інтервалів на електрокардіографічному комплексі «Кардиолаб»

Опис алгоритму аналізу ВСР поданий у додатку В.

Ультразвукові дослідження (УЗД) в акушерстві є найбільш достовірною та інформативною методикою серед інших клінічних методів в оцінці деяких аспектів перебігу нормальної вагітності та особливо під час її патології.

Під час розробки алгоритму УЗ діагностики в акушерстві необхідно враховувати основні підходи в даній області. У зв'язку з цим узагальнений алгоритм включає в себе такі етапи.

Етап 1. Введення необхідних даних про пацієнта та уточнення наявності вагітності, а також визначення одноплідної або багатоплідної вагітності.

Етап 2. Оцінка стану провізорних і родових органів вагітної з урахуванням розміру шийки матки, ширини цервикального каналу, розміру матки та її товщини, стадії зрілості плаценти, об'єму амніотичної рідини.

Етап 3. Визначення положення, позиції та виду плода.

Етап 4. Визначення росту плода з урахуванням біпариетального розміру голови, лобно-потиличного розміру голівки плоду, цефалічного індексу, довжини стегна та діаметра живота.

Етап 5. Оцінка життєдіяльності плода з урахуванням серцевих скорочень і рухової активності та екстраембріональних утворень з урахуванням оцінки жовчного міхура, жовчної протоки, амніотичної оболонки, хоріона та жовтого тіла вагітності.

Етап 6. Визначення та оцінка анатомії плода з урахуванням усіх органів та гестаційного терміну з урахуванням проксимального епіфіза стегна та дистального епіфіза великої голеневої кістки.

Етап 7. Оцінка біофізичного профілю плода за бальною шкалою Vintzileos з урахуванням дихальних рухів плода, тонусу плода, об'єму амніотичних вод, плаценти, рухової активності плода.

Схема узагальненого алгоритму УЗ-діагностики в акушерстві подана у додатку Г.

Несприятливі екологічні умови, що створилися в Україні, призвели до значного техногенного зараження землі, води атмосфери та через них і продуктів харчування цілим рядом радіоактивних речовин природного та штучного походження: цезій-134, радій-226, торій-232, калій-40. Тому екологічна обстановка вимагає постійного контролю та прогнозування радіаційної обстановки для зменшення ймовірності виникнення захворюваності у населення. Опис алгоритму методу аналізу впливу радіонуклідів на здоров'я людини та його схема наведені у додатку Д.

Контрольні запитання

1. Дайте визначення поняттям «формалізація» та «алгоритмізація».

2. Опишіть суть основних законів логіки.

3. Що таке формальна логіка та що вона вивчає?

4. Дайте визначення поняттю «мова».

5. Які основні правила запису складних суджень Вам відомі?

6. Наведіть основні закони алгебри висловлювань.

7. Що являє собою мова логіки предикатів? Які знаки (символи) включає алфавіт цієї мови?

8. Опишіть суть правил виведення modus ponens та modus tollens.

9. В чому полягає принцип резолюції?

10. У сукупності з якими методами міркування зазвичай застосовується резолюція в логічному програмуванні?

11. Дайте визначення поняттям «чітка множина» та «нечітка множина». Наведіть їх приклади.

12. Що таке функція приналежності?

13. Наведіть часто використовувані стандартні форми функцій приналежності.

14. Які дві групи методів використовують під час побудови за експертними оцінками функцій приналежності нечіткої множини? Опишіть їх.

15. Наведіть основні операції на нечітких множинах.

16. Дайте визначення поняттям нечіткої та лінгвістичної змінних.

17. Дайте визначення поняттю нечіткого відношення. Наведіть приклад нечіткого відношення.

18. Які основні етапи включає механізм логічного виведення? Опишіть їх суть.

19. Що називається алгоритмом?

20. Перелічіть і поясніть властивості алгоритму.

21. Яких правил слід дотримуватися під час складання структурної схеми алгоритму?

22. Охарактеризуйте основні методи розробки та аналізу алгоритмів.

23. Дайте визначення поняттю «діагностичний алгоритм».

24. Які основні форми запису діагностичного алгоритму Ви знаєте?

25. Наведіть приклади діагностичних алгоритмів, розроблених для МІС.