§8. Квадратичные формы

При изучении аналитической геометрии мы познакомились с элементами теории линий и поверхностей второго порядка. Их уравнения представляли собой алгебраические уравнения второго порядка относительно двух или трех переменных. Здесь мы соприкоснемся с их обобщением на случай n переменных, а так же научимся решать средствами линейной алгебры новые задачи по распознаванию кривых и поверхностей второго порядка. Рассмотрения будем проводить в рассматриваемом как арифметическое эвклидово пространство со скалярным произведением.

8.1. Симметрические операторы и их свойства.

Определение1Линейный оператор называется симметрическим, если для любых векторов выполняется .

Перечислим без доказательства основные свойства симметрических линейных операторов.

1. Линейный оператор является симметрическим тогда и только тогда, когда его матрица в любом базисе симметрична.

2. Собственные векторы симметрического линейного оператора, соответствующие различным собственным значениям, ортогональны.

3. Всякому собственному числу кратности k симметрического оператора соответствует линейно независимая система из k собственных векторов.

4. Для всякого симметрического линейного оператора существует базис в пространстве , состоящий из его собственных векторов. Последнее означает , что симметрический линейный оператор является оператором простой структуры и в базисе из собственных векторов его матрица имеет диагональный вид .

8.2. Матричная запись квадратичной формы.

Опр.Квадратичнойформой называется сумма где Подробнее эту сумму можно записать так:

Опр.Матрицей квадратичной формы называется матрица А с элементами , составленная из ее коэффициентов. Главное ее свойство – она симметрическая.

Пример. Найдите матрицу квадратичной формы .

Так как в сумме нет слагаемых с , то а₁₁ = а₂₂ = а₃₃ = 0. Так как 2а₁₂ = 2, 2а₁₃ = 1, 2а₂₃ = -6, то а₁₂ = 1, а₁₃ =0.5, а₂₃ = -3.

Ответ: .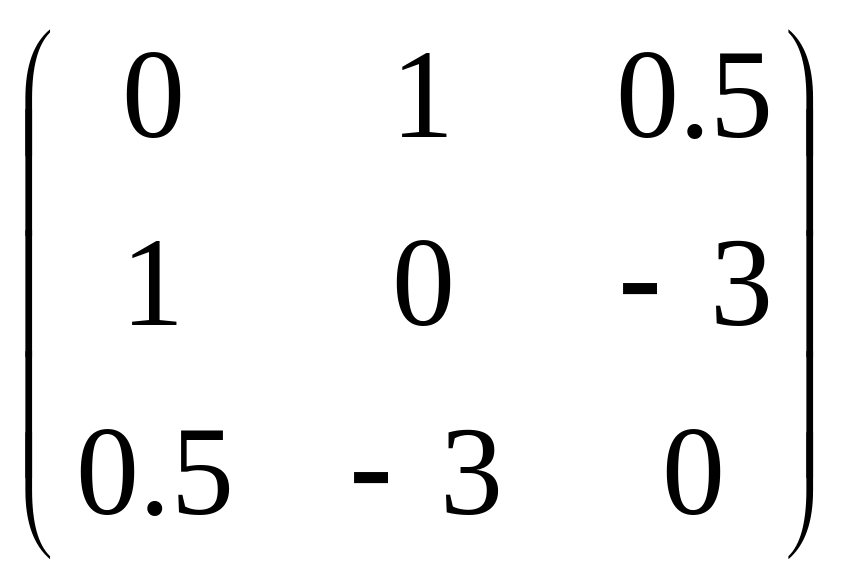

Теорема. (Матричная запись квадратичной формы).

Пусть Х столбец, составленный из переменных, А – матрица квадратичной формы f , тогда всякую квадратичную форму можно задать с помощью матрицы:

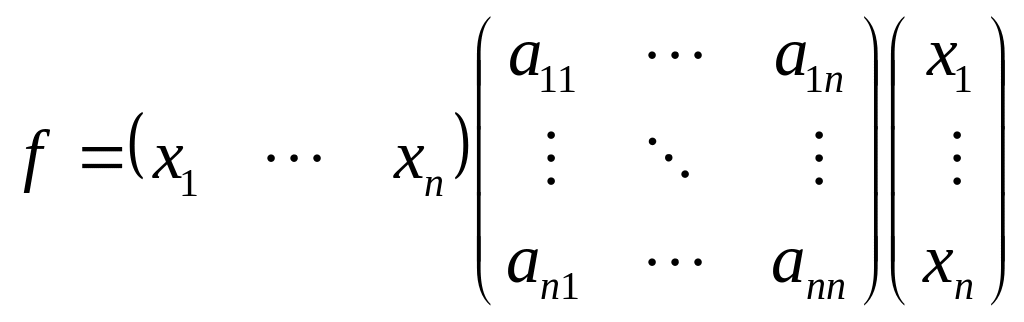
Доказательство.

АХ = .

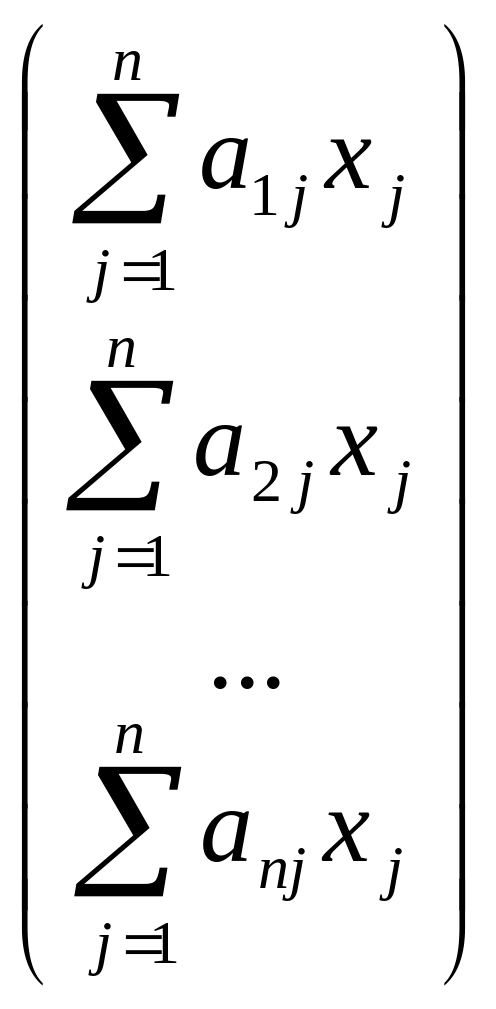Умножая обе части матричного равенства на матрицу Х^Т (транспонированную по отношению к X) слева, в правой части получим f : Х^Т AX=f.

Следствие.f=(AX,X)

8.3. Приведение квадратичных форм к каноническому виду.

Опр.Квадратичная форма имеет канонический вид, если в ее записи нет слагаемых с произведениями неизвестных, т. е. .

Теорема. (о приведении квадратичной формы к главным осям). Любую квадратичную форму с помощью преобразования переменных можно привести к каноническому виду.

Доказательство. Матрица А квадратичной формы симметрична, а для симметрического оператора всегда существует n собственных чисел, и, соответственно, n собственных векторов. Отсюда следует, что в новом базисе, составленном из этих собственных векторов, матрица оператора будет диагональной. Мы показали, что существует матрица Q, составленная из ортогональных собственных векторов А такая, что матрица Q^{- 1}AQ диагональна. Подвергнув квадратичную форму ортогональному преобразованию с матрицей Q, мы приведем ее к каноническому виду. ■

Следствие Квадратичная форма с помощью преобразования переменных приводится к каноническому виду, коэффициентами которого являются корни характеристического многочлена матрицы квадратичной формы, взятые с их кратностями.

Доказательство. f=(AX,X) , матрица А в базисе из собственных векторов имеет диагональный вид с собственными числами на главной диагонали.

Получили следующий алгоритм приведения квадратичной формы к каноническому виду:

1. Построить матрицу квадратичной формы.

2. Найти собственные числа и векторы, записать квадратичную форму (коэффициентами при квадратах новых переменных будут найденные собственные числа).

3. Нормировать собственные векторы и записать матрицу перехода от старого базиса к новому (а именно, состоящему из найденных векторов).

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

Решение: Составим характеристическое уравнение квадратичной формы : при

Решив это уравнение, получим ₁ = 2, ₂ = 6.

Найдем координаты собственных векторов:

полагая

m₁ = 1, получим n₁ =

полагая

m₂ = 1, получим n₂ =

Собственные векторы:

Находим координаты единичных векторов нового базиса.

Имеем следующее уравнение линии в новой системе координат:

Каноническое уравнение линии в новой системе координат будет иметь вид:

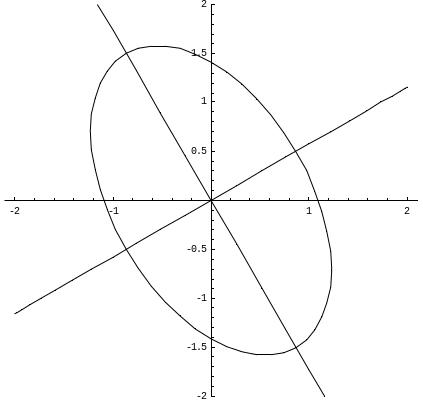
Кривая является эллипсом с полуосями

Матрица ортогонального преобразования Q составляется из координатных столбцов векторов :

Q = .

Легко проверить , что это матрица оператора поворота на

по часовой стрелке.

Выпишем линейное преобразование переменных, приводящее уравнение к каноническому виду (см.7.1.)

Остается схематично изобразить фигуру.

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

4ху + 3у² + 16 = 0

Коэффициенты: a₁₁ = 0; a₁₂ = 2; a₂₂ = 3.

Характеристическое уравнение:

Корни: ₁ = -1, ₂ = 4.

Для ₁ = -1 Для ₂ = 4

m₁ = 1; n₁ = -0,5; m₂ = 1; n₂ = 2;

= (1; -0,5) = (1; 2)

Получаем: -каноническое уравнение гиперболы.

Матрица преобразования Q составляется из координатных столбцов векторов :

Q = .

Легко проверить , что это матрица оператора поворота на

острый угол по часовой стрелке.

Выпишем линейное преобразование переменных, приводящее уравнение к каноническому виду (см.7.1.)

Остается схематично изобразить фигуру

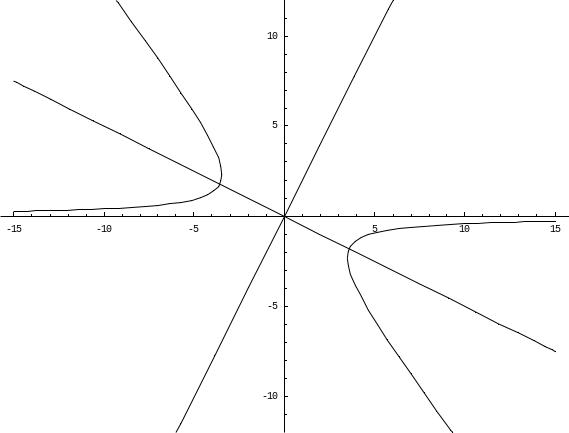
Канонический вид квадратичных форм используется для определения типа уравнений кривых и поверхностей второго порядка.

Пример. Привести к каноническому виду квадратичную форму

Ф(х₁, х₂) = 27 .

Коэффициенты: а₁₁ = 27, а₁₂ = 5, а₂₂ = 3.

Составим характеристическое уравнение: ;

(27 - )(3 - ) – 25 = 0

² - 30 + 56 = 0

₁ = 2; ₂ = 28;

Пример. Привести к каноническому виду уравнение второго порядка:

17x² + 12xy + 8y² – 20 = 0.

Коэффициенты а₁₁ = 17, а₁₂ = 6, а₂₂ = 8. А =

Составим характеристическое уравнение:

(17 - )(8 - ) - 36 = 0

136 - 8 - 17 + ² – 36 = 0

² - 25 + 100 = 0

₁ = 5, ₂ = 20.

Итого: - каноническое уравнение эллипса.