МIНIСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ЗАПОРІЗЬКИЙ ІНСТИТУТ ЕКОНОМІКИ І ІНФОРМАЦІЙНИХ ТЕХНОЛОГІЙ

Методическое пособие

к выполнению лабораторных работ

по дисциплине «оптимизационные методы и модели»

для студентов дневной формы обучения

Утверджено на заседании

кафедры прикладной математики.

Протокол№_______________

от “___” __________2013

Составители :

к.т.н., проф. Нудный И.П.

Запорожье 2013

Задания комплексного И.Д.З.

Задача 1. Для производства изделий А,В,С используется четыре вида сырья.Каждый из видов сырья может бать использован в количестве.соответственно не большем М_1,М₂,М₃,М₄.

Нормы затрат каждого из видов сырья на единицу продукции и цена единицы продукции заданы таблицей.

Вид сырья	Нормы затрат на единицу лродукции			Колич. сырья
	А	В	С
I	3	4	1	М1
II	2	5	3	М2
III	4	1	2	М3
IV	5	6	4	М4
Цена единицы продукции	N1	N2	N3

Лаб.раб. №1

Определить план выпуска продукции ,при котором обеспечивается ее максимальная стоимость, и найти эту стоимость.

Лаб.раб. №2

1.Определить,какой вид сырья необходимо приобрести дополнительно,чтобы увеличение прибыли было максимальным.

2.Найти зависимость максимальной стоимости продукции от количества сырья,ислользуемого полностью или с наименьшим остатком. Расчеты произвести для значений [M_i / 2, 2M_i ] с интервалом ∆M_i=3M_i/10. Здесь і-номер сырья,используемого максимально.

Лаб.раб. №3

3.Считая, что количество продукции может выражаться только в целых единицах,определить новый план выпуска продукции с учетом целочисленности.

Задача 2. (Лаб. раб. № 4) Задана матрица С стоимостей перевозки единицы товара, вектор производства а (количество товара, производимого каждым производителем), вектор потребления b (количество товара, потребляемого каждым потребителем ).

a = (a₁ a₂ a₃ a_{4 )}

C= b =( b₁ b₂ b₃ b₄ b₅ )

Составить план перевозок, чтобы суммарные транспортные расходы были минимальными.

Задача 3. (Лаб. раб. № 5) Задана матрица эффективностей С - матрица оценок выполнения заданных работ каждым работником (например, в пятибалльной системе) :

C=

Нужно распределить работников по работам так,чтобы все работы были выполнены при наибольшей эффективности.

Задача 4. (Лаб. раб. № 6) Полагая,что продукція производится в течении восьми месяцев, определить оптимальное количество работников в каждом месяце. Идеальное количество работников в i-ом месяце равно m_i (i=1-8). Допускается,что работа i-го месяца может быть выполнена и меньшим числом работников при сверхурочной работе. Затраты, связанные с изменением количества работников при переходе от (i-1)-го месяца к i-му определяются функцией f_i(x_i-x_i-1), где х_i – фактическое количество работников в i-м месяце. Отклонение количества работников в i-м месяце от m_i приводит к потерям

g (x_i-m_i). Первоначальное количество работников было m₀.

Оптимальным будем считать такое количество работников,при котором обеспечивается выполнение задания при минимальных суммарных потерях.

f_i(x_i-x_i-1) =

g_i(x_i-m_i) =

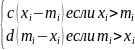
Задача 5. (Лаб. раб. № 7) Для производства изделий А и В используется три вида сырья.Каждый из видов сырья может бать использован в количестве соответственно не большем М_1,М₂,М₃.

Нормы затрат каждого из видов сырья на единицу продукции и цена единицы продукции заданы таблицей.

Вид сырья	Нормы затрат на единицу лродукции
	А	В
I	3	4
II	2	5
III	4	1
Цена едницы продукции	5N1	5N2

Общие расходы на производство единицы продукции вида А равны х₁, а на производство единицы продукции вида В равны 2х₂, где х₁-количество единиц продукции вида А, х₂-количество единиц продукции вида В.

Составить план производства, чтобы получить максимальную прибыль.

Исходные данные к лабораторным работам №1-№3, №7

Вариант	М1	М2	М3	М4	N1	N2	N3
1	80	120	60	90	8	12	6
2	60	100	160	80	6	7	9
3	120	70	90	80	9	7	12
4	90	50	140	100	7	12	9
5	120	90	70	260	9	6	3
6	110	180	200	60	8	14	10
7	70	150	230	90	10	6	8
8	100	240	280	120	9	8	6
9	80	60	90	120	5	4	6
10	200	130	80	60	8	4	10
11	120	160	100	90	6	9	12
12	90	100	140	80	10	5	9
13	50	40	70	100	4	12	6
14	130	80	50	200	5	8	4
15	140	190	70	60	6	12	10
16	80	100	220	90	3	6	5
17	160	120	60	100	8	9	4
18	150	90	210	180	6	8	12
19	140	90	200	80	5	15	10
20	200	80	70	120	5	4	4
21	80	110	90	160	6	4	9
22	190	230	90	80	4	6	8
23	150	180	70	110	9	12	6
24	60	90	130	120	3	5	4
25	90	120	150	80	9	8	6

Исходные данные к лаб. раб.№4.

= ( N 30 10 45 ) = ( 20 25 15 10 2N )

С=

где N – номер варианта ,

К =

Исходные данные к лаб. раб.№5

1≤ N≤ 5 6≤ N≤ 10 11≤ N≤ 15

C= C= C=

16≤ N≤ 20 21≤ N≤ 25

C= C=

N – номер варианта

Исходные данные к лаб. раб.№6.

Вари ант	a1	a2	b1	b2	m0	m1	m2	m3	m4	m5	m6	m7	m8	m9	m10	m11	m12
1	5	4	3	6	1	3	5	8	4	2	7	5	2	4	5	7	3
2	3	5	6	4	4	9	4	3	5	7	3	4	1	5	8	4	5
3	5	7	4	8	4	2	6	8	5	4	6	3	6	9	4	6	2
4	9	4	6	8	2	5	3	9	4	4	7	3	1	5	4	9	6
5	4	7	7	6	0	3	5	2	6	3	4	2	4	8	5	1	4
6	8	6	7	8	3	2	1	5	0	4	2	3	7	5	9	4	2
7	7	9	8	6	4	1	3	2	5	0	4	3	9	5	2	6	3
8	6	7	9	6	1	5	2	4	3	8	2	0	4	1	5	3	1
9	8	7	7	5	2	4	3	0	5	2	7	5	4	9	4	3	5
10	4	8	6	5	3	2	5	1	4	3	2	4	6	4	9	3	5
11	7	6	5	9	4	3	1	4	2	5	3	3	8	4	6	2	5
12	4	6	5	8	5	2	3	5	1	4	7	2	4	8	6	3	4
13	6	5	7	6	2	5	0	4	3	5	1	4	8	3	5	3	1
14	8	9	6	8	4	2	3	5	1	4	9	3	6	4	5	3	5
15	5	7	8	6	0	4	1	3	2	5	8	4	2	6	8	9	4
16	3	6	9	7	3	1	5	2	3	7	4	2	3	5	9	6	8
17	9	7	7	8	1	4	2	5	3	2	4	7	3	5	6	9	4
18	7	9	8	6	4	1	3	2	0	5	2	3	9	6	8	5	2
19	5	9	8	7	2	3	4	1	5	2	4	9	4	3	5	6	3
20	4	8	7	9	1	5	2	4	1	4	3	0	7	5	2	4	8
21	8	6	9	7	3	1	5	2	4	0	3	7	4	3	9	5	3
22	5	4	8	9	1	4	1	3	2	5	3	9	4	6	3	5	2
23	6	5	6	9	4	1	3	2	4	0	5	8	3	6	2	5	4
24	9	6	5	8	2	4	1	5	3	9	4	1	3	7	4	6	3
25	7	6	5	8	4	3	5	1	4	2	4	3	8	5	7	4	5

Лабораторная работа № 1.