РОЗДІЛ 1. ЛІНІЙНІ ЕЛЕКТРИЧНІ КОЛА ЗА ПОСТІЙНИХ СТРУМІВ

Тема 1.1. Основні поняття і закони електричного кола

Лекція №1

Електричне поле Основні поняття

Всі тіла складаються з молекул, а молекули з атомів, до складу яких входять елементарні частинки: позитивно заряджені протони, негативно заряджені електрони та нейтральні частинки – нейтрони. Ці частинки або входять до складу молекули або є “вільними”. В звичайних умовах тіло має рівну кількість позитивних та негативних заряджених частинок, тобто рівну кількість позитивних та негативних електричних зарядів, таке тіло є нейтральним. У випадку коли в тілі (його частині) кількість позитивних або негативних електричних зарядів переважає, його вважають електрично зарядженим тілом.

Примітка:

Електричний заряд – це фізична величина, що характеризує властивість частинок або тіл вступати в електромагнітні силові взаємодії.

Електричний заряд зазвичай позначається літерою q або Q.

Сукупність всіх відомих експериментальних фактів дозволяє зробити наступні висновки:

• Існують два види електричних зарядів, умовно названих позитивними й негативними.

• Заряди можуть передаватися (наприклад, при безпосередньому контакті) від одного тіла до іншого. На відміну від маси тіла електричний заряд не є невід'ємною характеристикою даного тіла. Одне й те саме тіло в різних умовах може мати різний заряд.

Однойменні заряди відштовхуються, різнойменні – притягаються.

Якщо два електрично заряджені тіла знаходяться на малій відстані, то між ними виникають сили електричної взаємодії. Таку взаємодію можна пояснити тим, що кожна з частинок нерозривно пов’язана з оточуючим її електричним полем. Електричні заряджені частинки та електричне поле є видами матерії. Якщо в електричне поле, яке оточує електрично заряджену частинку речовини, внести іншу заряджену частинку, то остання буде відчувати дію сили поля; в свою чергу електричне поле другої частинки буде діяти на першу частинку.

Таким чином, взаємодія заряджених тіл здійснюється не безпосереднім їхнім впливом один на одного, а через електричні поля, що оточують заряджені тіла.

Для кількісного визначення електричного поля вводиться силова характеристика – напруженість електричного поля.

Напруженістю електричного поля називають фізичну величину, рівну відношенню сили, з якої поле діє на позитивний пробний заряд, поміщений у дану точку простору, до величини цього заряду:

(1.1)

Напруженість електричного поля – векторна фізична величина. Напрямок вектора у кожній точці простору збігається з напрямком сили, що діє на позитивний пробний заряд.

Електричне поле нерухомих і незмінних у часі зарядів називається електростатичним. У багатьох випадках для зручності це поле позначають загальним терміном – електричне поле (ЕП).

Якщо за допомогою пробного заряду досліджується електричне поле, створюване декількома зарядженими тілами, то результуюча сила виявляється рівною геометричній сумі сил, що діють на пробний заряд з боку кожного зарядженого тіла окремо. Отже, напруженість електричного поля, створюваного системою зарядів у даній точці простору, дорівнює векторній сумі напруженостей електричних полів, створюваних у тій же точці зарядами окремо:

(1.2)

Ця властивість електричного поля означає, що поле підкоряється принципу суперпозиції.

Відповідно до закону Кулона напруженість електростатичного поля, створювана точковим зарядом Q₁, на відстані R від нього (наприклад, в точці з точковим зарядом Q₂), дорівнює по модулю

(1.3)

Примітка:

В знаменнику замість квадрату відстані R від даної точки до точкового заряду Q₁ введена величина поверхні кулі , яка проходить через точку з точковим зарядом Q₂, та має центр у точці з точковим зарядом Q₁.

Величина ε_а – є величиною, яка враховує вплив середовища та називається її абсолютною діелектричною проникністю.

Абсолютна діелектрична проникність різних речовин – різна. Експериментально встановлено, що абсолютна діелектрична проникність вакууму ε₀=8,85·10^-12 Ф/м. Її (ε₀) ще називають електричною постійною.

Абсолютну діелектричну проникність речовин зручно виражати, через електричну постійну. Відношення ε= ε_а/ε₀ називають відносною діелектричною проникністю речовини.

Поле точкових заряді називається кулонівським. У кулонівському полі напрямок вектора залежить від знака заряду Q:

• якщо Q > 0, то вектор спрямований по радіусі від заряду;

• якщо Q < 0, то вектор спрямований до заряду.

Для наочного зображення електричного поля використають силові лінії. Ці лінії проводять так, щоб напрямок вектора у кожній точці збігався з напрямком дотичної до силової лінії (рис. 1.1). При зображенні електричного поля за допомогою силових ліній, їхня густота повинна бути пропорційна модулю вектора напруженості поля.

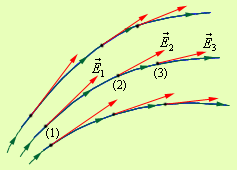
Рис. 1.1. Силові лінії електричного поля

Силові лінії кулонівських полів позитивних і негативних точкових зарядів зображені на рис. 1.2. Оскільки електростатичне поле, створюване будь-якою системою зарядів, може бути представлене у вигляді суперпозиції кулонівських полів точкових зарядів, то зображені на рис. 1.2 поля можна розглядати як елементарні структурні одиниці (“цеглинки”) будь-якого електростатичного поля.

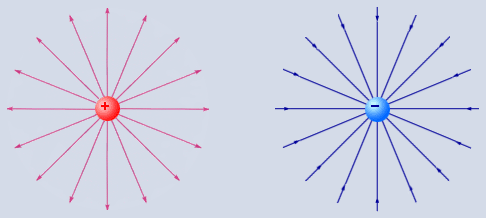
Рис. 1.2. Силові лінії кулонівських полів

Кулонівське поле точкового заряду Q зручно записати у векторній формі. Для цього потрібно провести радіус-вектор від заряду Q до точки спостереження. Тоді при Q > 0 вектор паралельний , а при Q < 0 вектор антипаралельний . Отже, можна записати:

(1.4)

де R – модуль радіуса-вектора .

Як приклад застосування принципу суперпозиції полів на рис. 1.3. зображено картину силових ліній поля електричного диполя – системи із двох однакових по модулі зарядів різного знака q й –q, розташованих на деякій відстані l.

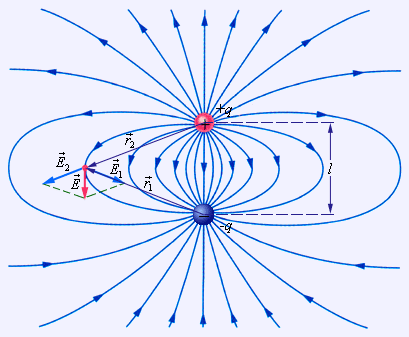
Рис. 1.3. Силові лінії поля електричного диполя

Примітка:

Загальні властивості силових ліній ЕП:

1. Починаються на позитивних й закінчуються на негативних зарядах.

2. Не перетинаються.

3. Густота ліній тим більше, чим більша напруженість. Таким чином напруженість поля прямо пропорційна кількості силових ліній, що проходять через одиницю площі поверхні.

Важливою характеристикою електричного диполя є так званий дипольний момент :

(1.5)

де – вектор, спрямований від негативного заряду до позитивного, модуль . Диполь може служити електричною моделлю багатьох молекул.

Електричним дипольним моментом володіє, наприклад, нейтральна молекула води (H₂O), тому що центри двох атомів водню розташовуються не на одній прямій із центром атома кисню, а під кутом 105° (рис. 1.4). Дипольний момент молекули води p = 6,2·10^–30 Кл · м.

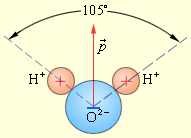
Рис. 1.4. Дипольний момент молекули води

У багатьох задачах електростатики потрібно визначити електричне поле по заданому розподілі зарядів. Нехай, наприклад, потрібно знайти електричне поле довгої однорідної зарядженої нитки (рис. 1.5) на відстані R від неї.

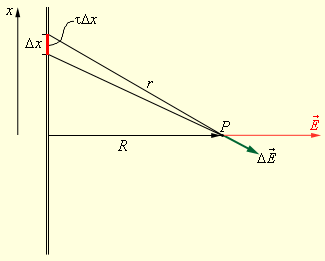
Рис. 1.5. Електричне поле зарядженої нитки

Поле в точці спостереження P може бути представлене у вигляді суперпозиції кулонівських полів, створюваних малими елементами Δx нитки, із зарядом τΔx, де τ – заряд нитки на одиницю довжини. Завдання зводиться до сумування (інтегрування) елементарних полів . Результуюче поле виявляється рівним

Вектор скрізь спрямований по радіусу . Це витікає із симетрії задачі. Уже цей простий приклад показує, що прямий шлях визначення поля по заданому розподілу зарядів приводить до громіздких математичних викладок. У ряді випадків можна значно спростити розрахунки, якщо скористатися теоремою Гаусса, яка виражає фундаментальну властивість електричного поля.

Ця теорема встановлює зв'язок між векторним полем Е і величиною заряду, який створює це поле.

Для того щоб сформулювати теорему Гауса введемо нову фізичну величину, що характеризує електричне поле – потік Φ вектора напруженості електричного поля. Нехай у просторі, де створене електричне поле, розташована деяка досить мала площадка ΔS. Добуток модуля вектора на площу ΔS і на косинус кута α між вектором і нормаллю до площадки називається елементарним потоком вектора напруженості через площадку ΔS (рис. 1.6):

ΔΦ = E ΔS cos α = E_n ΔS (1.6)

де E_n – модуль нормальної складового поля .

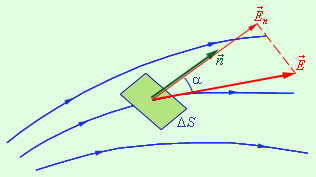
Рис. 1.6. До визначення елементарного потоку ΔΦ

Розглянемо тепер деяку довільну замкнену поверхню S. Якщо розбити цю поверхню на малі площадки ΔS_i, визначити елементарні потоки ΔΦ_i поля через ці малі площадки, а потім їх просумувати, то в результаті ми отримаємо потік Φ вектора через замкнену поверхню S (рис. 1.7):

.

У випадку замкненої поверхні завжди обирається зовнішня нормаль.

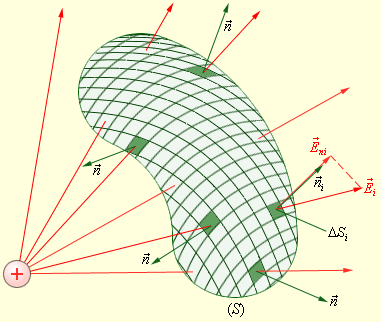
Рис. 1.7. Обчислення потоку Ф через довільну замкнену поверхню S

Теорема Гаусса стверджує: потік вектора напруженості електростатичного поля через довільну замкнену поверхню дорівнює алгебричній сумі зарядів, розташованих усередині цієї поверхні, діленої на електричну постійну ε_0.

, (1.7)

де ,

– щільність заряду.

Математично теорема Гаусса у вакуумі записується так

• в інтегральній формі .

Примітка:

Теорема Гаусса в інтегральній формі пов’язує потік вектора ЕП із сумарним зарядом, зосередженим усередині об’єму.