Розділ 8 Чисельне розв’язання звичайних диференціальних рівнянь

Звичайними диференціальними рівняннями називаються рівняння, що пов’язують функцію та її похідні з однією незалежною змінною. Якщо незалежних змінних більше, ніж одна, то рівняння називається диференціальним рівнянням з частинними похідними.

За допомогою звичайних диференціальних рівнянь будуються моделі руху систем взаємодіючих часток, електротехнічних процесів у електричних ланцюгах, кінетики хімічних реакцій, процесів заселення рівнів енергії у високотемпературних середовищах і багатьох інших об'єктів і процесів.

До задач для звичайних диференціальних рівнянь зводяться деякі задачі для рівнянь у частинних похідних, коли рівняння дозволяє провести відокремлення змінних (наприклад, при обчисленні енергетичного спектра часток у полях визначеної симетрії).

Звичайне диференціальне рівняння будь-якого порядку за допомогою заміни змінних може бути зведене до системи рівнянь першого порядку.

У загальному вигляді перетворення є таким:

диференціальне рівняння -го порядку

заміною змінних зводяться до системи рівнянь першого порядку

де позначено .

Відповідно до викладеного далі будуть розглядатися системи рівнянь першого порядку:

Розв’язок системи -го порядку залежить від параметрів Єдиний розв’язок визначається при використанні додаткових умов для шуканої функції. У залежності від того, яким чином ставляться такі умови, розрізняють три типи задач для звичайних диференціальних рівнянь: задача Коші, крайова задача і задача на власні значення.

У задачі Коші всі додаткові умови ставляться в одній точці . Розв’язок шукається на деякому інтервалі

Якщо праві частини рівнянь неперервні в деякому околі початкової точки і задовольняють умову Ліпшиця за змінними , то розв’язок задачі Коші існує, єдиний і неперервно залежить від координат початкової точки, тобто задача є коректною. Умова Ліпшиця формулюється в такий спосіб:

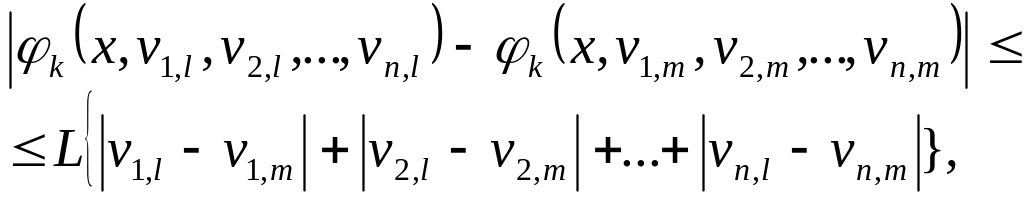
для будь-яких точок , де - деяка константа.

Можна виділити три класи методів розв’язання звичайних диференціальних рівнянь: точні, наближені та чисельні.

Точні методи передбачають одержання розв’язку у вигляді комбінації елементарних функцій або у вигляді квадратур від останніх. Можливості точних методів обмежені.

Наближені методи зводяться до побудови послідовності функцій , що мають границею шукану функцію . Обриваючи цю послідовність на якомусь , одержують наближений розв’язок.

Найбільш універсальними методами розв’язання є чисельні. Їхній основний недолік - можливість одержання тільки часткового розв’язку.

Варто зауважити, що успіх від застосування чисельного методу суттєво залежить від обумовленості задачі, тобто задача повинна бути добре обумовленою, а саме, малі зміни початкових умов повинні призводити до малих змін у розв’язку. У протилежному випадку (слабкої стійкості) малі похибки в початкових даних або похибки чисельного методу можуть призводити до великих похибок у розв’язку.

Приклад. Рівняння з початковою умовою має розв’язок .

При виходить розв’язок . Якщо припустити, що не дорівнює строго нулеві, а має невелике відхилення від нуля, наприклад, , тоді при великих буде мати місце така ситуація.

Якщо , то при збільшенні прямує до нуля, тобто до незбуреного розв’язку. У цьому випадку розв’язок називається асимптотично стійким за Ляпуновим.

Однак при зі збільшенням необмежено зростає, а саме, наприклад, при .

Таким чином, розв’язок виявляється нестійким.

Далі будуть розглядатися алгоритми розв’язку задачі Коші на прикладі одного рівняння першого порядку . Узагальнення на випадок системи рівнянь здійснюється заміною на і на , де

, .