§ 2. Графический метод решения тригонометрических уравнений

Приведем примеры, применения графического метода решения тригонометрических уравнений и неравенств, который дает возможность определить корни намного проще, чем при аналитическом способе решения.

Пример 6. Решите уравнение: cos t = 2^{sin t} – 1.

Дополним уравнение тождеством sin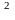 t + cos t = 1 и рассмотрим систему двух уравнений:

Введём обозначения x = cos t, y = sin t и решим графически систему, состоящую из двух уравнений:

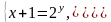
Рис. 8

Графическое решение системы показано на рис. 8. Проведя радиус-векторы точек пересечения единичной окружности с графиком y = log₂(x+1), получим:

α₁ 48^°

α₂ -117^°

t₁ = α₁ + 360^°n t₁ = 48^° +360^°n

t₂ = α₁ + 360^°n t₂ = -117^° + 360^°n, где n, k Z.

Пример 7. Решите уравнение: 8tg t – 4ctg² t – 4ctg t + 23 = 0.

Дополним уравнение тождеством ctg t · tg t = 1 и рассмотрим систему двух уравнений:

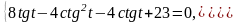
Введём обозначения x = ctg t, y = tg t и решим графически систему, состоящую из двух уравнений:

Преобразуем первое уравнение системы:

y = 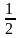(x² + x - ) = ((x² +2∙x∙ + ) - - ) = ((x + )² – 6) =

= (x + )² – 3.

Рис. 9

Графическое решение системы показано на рис. 9

По рис. 9 находим: α₁ ≈ 25^°, α₂ ≈ -20^°, α₃ ≈ -71^°.С учетом периодичности: t₁ = 25^° + 360^°n; t₂ = -20^° + 360^°k; t₃ = -71^° + 360^°m, где n, k, m Z.

§ 3. Графический метод решения тригонометрических неравенств

Пример 8. Решите неравенство:

8cos³ t – 14cos² t + 6cos t – 2sin² t + 8sin t – 3 ≥ 0

Заменим sin² t = 1 – cos² t.

8cos³ t – 14cos² t + 6cos t – 2 + 2cos² t + 8sin t – 3 ≥ 0

8cos³ t – 12cos² t + 6cos t + 8sin t – 5 ≥ 0

Пусть sin t = y, cos t = x

8x³ – 12x² + 6x + 8y – 5 ≥ 0

8y ≥ -8x³ + 12x² – 6x + 5

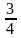y ≥ -x³ + x² - x +

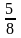
y ≥ -(x³ - x² + x - )

y ≥ -((x³ – 3∙x²∙ + 3∙x∙ - ) + - )

y ≥ -((x - )³ - )

О стается решить графически систему, состоящую из неравенства (3) и из уравнения x² + y² = 1.

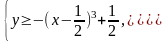
Рис. 10

Выделенная на рис. 10 дуга единичной окружности и является графическим решением этой вспомогательной системы.

Каждая точка этой дуг имеет радиус-вектор, образующий с положительным направлением оси Ox угол, величина которого изменяется в промежутке [26^°; 106^°]. Учитывая периодичность, получаем t [26^°+ 360^°k; 106^°+360^°k], где k Z.

Пример 9. Решите неравенство: 2tg t + ctg² t – 2ctg t – 4 < 0

Введем обозначения и приведем неравенство к виду, удобному для построения графика:

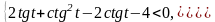
Преобразуем первое уравнение системы:

2y + x² – 2x – 4 < 0

2y < - x² + 2x + 4

y < - x² + x + 2

y < - (x² – 2x – 4)

y < - ((x² – 2x + 1) – 1 – 4)

y < - ((x – 2)² – 5)

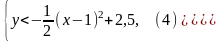
Решим графически систему, состоящую из неравенства(4) и уравнения

xy = 1.

Рис. 11

Этой системе удовлетворяют координаты точек, выделенных на гиперболе (рис. 11):

t [-90^°; t₃],

t [t₁; t₂].

Вспомним теперь о введении первоначального обозначения y = tg t и выделим на оси тангенсов промежутки, состоящие из точек, чьи ординаты такие же, как и ординаты пунктирной части гиперболы.

Углы, которые составляют радиус-векторы точек, лежащих на отрезке AB и на луче CE линии тангенсов, и является решением исходного неравенства, т.е. t [-90^°; -33^°] или t [18^°; 67^°].

При записи окончательного ответа следует учесть периодичность:

t [-90^° + 180^°k; -33^° + 180^°k] или

t [18^° + 180^°n; 67^° + 180^°n], n, k Z.

В заключение приведем ряд уравнений и неравенств, которые удобно решать рассмотренным методом:

1. sin t + 2cos² t – 4cos t – 1 = 0

2. 2sin t + cos­­_­­­­­³ t = 1

3. 2tg t – ctg³ t = 2

4. cos t – 2^{sin t – 1} = 0

5. sin t + 1 < 2^-1 e ^{cos t}

6. 4sn t + 2cos³ t ≤ 1

7. tg t + 1 = 2^{ctg t + 1}

8. sin t – 2sin² (2cos t) > 0