7.4.1 Индуктивный фильтр

Принципиальная схема L-фильтра приведена на рисунке 7.11а. Для постоянной составляющей тока сопротивление L-фильтра мало и потери на фильтре будут минимальными. Для переменных составляющих сопротивление индуктивности равно:

Х_L = L .

Очевидно, что переменное напряжение будет перераспределяться между фильтром и нагрузкой. При условии, что

L >> R_н ,

переменная составляющая на нагрузке будет гораздо меньше, чем на входе фильтра. Для вывода количественных соотношений воспользуемся эквивалентной схемой (рисунок 7.11б).

а б

а – принципиальная схема; б – схема замещения

Рисунок 7.11 – L - фильтр

Входной сигнал представим в виде двух составляющих: постоянной (U₀) и переменной (U_n). На нагрузке также будет присутствовать постоянная (U'₀) и переменная (U'_n) составляющие. Коэффициенты пульсации на входе и выходе фильтра определяются соотношениями:

К_nвх = U_n/U₀; К_nвых  = U^'_n/U^'₀ .

Определим постоянную (I₀) и переменную (I_n) составляющие тока в цепи:

(7.41)

где m – число фаз выпрямителя;

r_ф –- активное сопротивление индуктивности.

Тогда U'₀, U'_n будут равны:

U'₀ = I₀ * R_н = (U₀ ^. R_н)/(R_н + r_ф);

. (7.42)

Найдем значение коэффициента пульсации на выходе, используя (7.42):

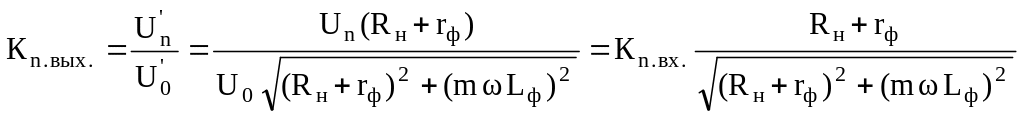. (7.43)

Из (7.43) определим Ксгл.:

. (7.44)

После преобразования можно получить соотношение

,

откуда – . (7.45)

С учетом того, что r_ф << R_н, а К_сгл >> 1 выражение (7.45) можно записать в виде

L  (К_сгл ^. R_н)/(m) . (7.46)

7.4.2 Емкостной фильтр

Схема фильтра приведена на рисунке 7.12а.

а б

а – принципиальная схема; б – форма напряжения на нагрузке.

Рисунок 7.12 – С - фильтр

Работа емкостного фильтра основана на явлении заряда и разряда емкости. При соответствующем соотношении R_н, R_фв, C амплитуда пульсаций на нагрузке уменьшается. Анализ процессов, происходящих при этом, проведен при рассмотрении работы выпрямителя на активно-емкостную нагрузку (рисунок 7.8б) и там же приведено соотношение для расчета К_пн (7.34). Более простое выражение для расчета К_пн получается исходя из предположения, что энергия, запасаемая в емкости при заряде, равна энергии, выделяемой при разряде. Исходя из рисунка 7.12б, можно записать:

. (7.48)

Отсюда можно определить С:

С = 10^б/(2mf_сR_н) ^. К_пн [мкф] . (7.49)

Допущения, сделанные при выводе (7.49), незначительно влияют на результат: при К_пн < 10% погрешность не превышает 10%. При К_пн > 10% необходимо пользоваться выражением (7.34).

7.4.3 Г-образные фильтры

LC-фильтр

Схема фильтра типа LC приведена на рисунке 7.13а.

а

К_сгл = mСR

б

а – LC-фильтр; б – RC-фильтр.

Рисунок 7.13 – Г-образные фильтры

Определим величину К_сгл для LC фильтра через величины элементов L и C. Переменная составляющая тока будет равна:

I_н = U_н/Z ,

где Z – входное сопротивление фильтра.

Переменная составляющая напряжения на нагрузке

U'_n = I_n ^. Z' = U_n(Z'/Z),

где Z' – выходное сопротивление фильтра.

Пренебрегая потерями в фильтре (U₀ = U'₀), можно записать:

К_сгл = К_n/К_nн = U_n/U'_n = Z/Z'.

Если учесть, что сопротивление фазы выпрямителя много меньше реактивного сопротивления фильтра, а R_н > 1/C, то получим:

Z' = 1/mC;  Z = mL – 1/mC .

В этом случае модуль коэффициента сглаживания определится соотношением

К_сгл =Z/Z' = (mL - 1/mC)/(1/mC) = m²²LC – 1 , (7.50)

откуда:

L ^. C = (К_сгл + 1)/(m²²) . (7.51)

При выборе величины L и C задаются одной величиной и по (7.51), зная К_сгл, расчитывают второй параметр. Для того чтобы нагрузка на выпрямитель носила индуктивный характер, т.е. не было разрывов тока диодов, величина L должна быть больше критической (L_кр). Обычно L выбирают равную 2L_кр, которую называют оптимальной (L_опт). Оптимальная индуктивность определяется соотношением

. (7.52)

Выбор величины емкости осуществляют из условия х_с < 0.2R_н. Значение С определяют из выражения

. (7.53)

Кроме этих требований, необходимо, чтобы собственная резонансная частота фильтра, равная:

_рф = 1/ ,

была намного ниже частоты первой гармонии.

На рисунке 7.13б приведена схема RC-фильтра. Рассуждая аналогично предыдущему, для К_сгл можно получить соотношение:

.

Необходимо отметить, что в RC-фильтрах потери гораздо выше, чем в LC-фильтрах и их используют преимущественно в маломощных источниках питания.

7.4.4 П-образные фильтры.

На практике наибольшее распространение получили П-образные фильтры типа CLC. Схема фильтра типа CLC приведена на рисунке 7.14а.

К_сгл = К_сгл1 * К_сгл2

а б в

а – СLС-фильтр; б – частотная характеристика; в – нагрузочная характеристика.

Рисунок 7.14 – Сложные фильтры и характеристики фильтров

Для расчета коэффициента сглаживания его представляют в виде последовательно соединеных С- и СL-фильтров. Общий коэффициент сглаживания определяется произведением

К_сгл = К_сгл1 ^. К_сгл2 . (7.55)

Это следует из следующих рассуждений. Пусть потери в фильтре малы, т.е. U₀  U'₀ U''₀, тогда

К_сгл = U_n/U'_n, а К_сгл2 = U'_n/U_n

и К_сгл = U_n/U''_n = К_сгл1 ^. К_сгл2 .

Если последовательно соединить n фильтров, то общий К_сгл равен:

К_сгл = К_сгл1 ^. К_сгл2 ^. ... ^. К_сглn . (7.56)