7.2.8 Работа выпрямителя на активно-емкостную нагрузку

Такой вид нагрузки является наиболее распространенным в источниках питания электронных схем, так как нагрузкой выпрямителя служит пассивный сглаживающий фильтр, первым элементом которого является емкость. Схема выпрямителя и диаграммы токов и напряжений приведены на рисунке 7.8.

В положительный полупериод, наряду с током, протекающим через нагрузку, происходит заряд емкости С_н. В соответствии с законами коммутации напряжение на емкости отстает от тока. В момент времени, когда U_с будет равно по величине питающему, диод VD закроется (т.е. раньше окончания положительного полупериода) и емкость начнет разряжаться. Сопротивление нагрузки гораздо больше сопротивления фазы выпрямителя (приведенное сопротивление трансформатора и сопротивление вентиля в открытом состоянии), поэтому постоянная разряда емкости больше постоянной заряда. Напряжение на емкости (нагрузке) будет медленно уменьшаться по ЕХР-закону. Повторное включение диода произойдет не в момент начала положительного полупериода, а несколько позже, когда U₂ превысит U_с. Происходит подзаряд емкости, и далее процессы повторяются. Таким образом, ток через диод протекает только в промежуток времени от t₁ до t₂. Угол, соответствующий половине периода протекания тока, называется углом отсечки (₁).

Для расчета выпрямителей с емкостной реакцией нагрузки используют графо-аналитический метод. Напряжение на вторичной обмотке трансформатора описывается выражением

U₂ = U_m cost . (7.24)

В момент времени, когда происходит отсечка тока диода, напряжение на нагрузке равно:

U₀ = U_2m cos ₁ . (7.25)

а б

а – схема; б – диаграммы токов и напряжений

Рисунок 7.8 – Работа выпрямителя на активно-емкостную нагрузку

Мгновенное значение тока нагрузки (диода) во вторичной обмотке определяется соотношением:

I₂ = (U₂ – U₀)/R_фв , (7.26)

где R_фв = r_тр + r_д – сопротивление фазы выпрямителя.

После замены U₂ и U₀ из (7.24) и (7.25) получим:

. .(7.27)

Постоянная составляющая разложения i₂ в ряд Фурье будет равна:

. (7.28)

Если в (7.28) подставить значение U_2m из (7.25), равное:

U_2m = U₀/cos₁, то получим (7.29)

где А = tg₁ - ₁.

Из (7.29) можно определить А следующим образом:

. (7.30)

График зависимости ₁ = (A) приведен на рисунке 7.9а.

Рассуждая аналогично, как и для выпрямителя, работающего на активную нагрузку, только с учетом отсечки тока диода, получены соотношения для расчета основных параметров:

U₂ = = U₀ В(₁) ; (7.31)

; (7.32)

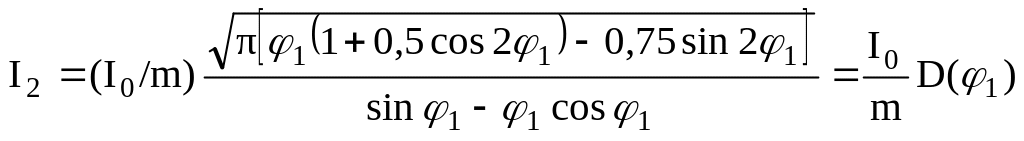. (7.33)

На практике при расчетах используют не зависимость коэффициентов B,F,D от ₁, а их зависимость от коэффициента А. Графики зависимостей B,F,D от А приведены на рисунке 7.9.

Алгоритм расчета выпрямителя с емкостной реакцией нагрузки следующий. Определяется сопротивление фазы выпрямителя, затем коэффициент А. Зная А, определяют коэффициенты B,F,D. Затем, используя основные расчетные соотношения, приведенные в таблице 7.3, определяют значения токов и напряжений.

График зависимости Н = f(A) используется при расчете коэффициента пульсации в соответствии с соотношением

.

Если расчет ведется на частоте 50 Гц и С_н взята в МкФ, то

. (7.34)

Рисунок 7.9 – Графики для определения коэффициентов. Расчет выпрямителей с активно-емкостной нагрузкой

Таблица 7.3 – Расчетные соотношения для определения

параметров выпрямления

Схема	П а р а м е т р ы
	m	Iд	Iдm	Uобр	U2	I1	I1	Ртр
Однофазная однотактная	1	DIo	FIo	2,82 BUo	BUo	DIo
Мостовая	2	0,5DIo	0,5 FIo	1,41 BUo	BUo	0,71 DIo		0,71 DP0
полумостовая	2	0,5DIo	0,5 FIo	2,82 BUo	BUo	0,5DIo		0,85 DP0
Трехфазная однотактная	3	0,33DIo	0,33 FIo	2,44 BUo	BUo	0,33 DIo		0,91 DP0
Трехфазная двухтактная	6	0,236DIo	0,33 FIo	1,22 BUo	0,58 Uo	0,33 DIo		0,58 DP0