3.3.2 Дифференцирование и интегрирование сигнала

В тех случаях, когда к выполнению операций не предъявляются жесткие требования к качественным характеристикам, дифференцирование и интегрирование можно осуществить с помощью пассивных элементов. Работа интегрирующего и дифференцирующего звеньев основана на использовании известных из курса теоретических основ электротехники соотношении:

(3.6)

Схемы дифференцирующих цепочек с применением емкости и индуктивности приведены на рисунке 3.5г.

При использовании емкости

U_вых = U_R = R ^. i_с = R ^. С . (3.7)

Так как U_с = U_вх – U_вых , то

U_вых = RC . (3.8)

Если . (3.9)

Анализ (3.8) показывает, что для уменьшения погрешности дифференцирования необходимо уменьшать постоянную времени  = RC.

Коэффициент передачи дифференцирующей цепи можно определить следующим образом:

(3.10)

где _н = 2f_н = 1/RC = 1/ – частота, при которой активное и реактивное сопротивление равны по модулю, т.е. R = 1/c.

 = RC – постоянная дифференцирования.

Модуль коэффициента передачи определится соотношением

(3.11)

а фазовый сдвиг –  = arctg(f_н/f) (3.12)

Соотношения (3.11) и (3.12) описывают амплитудно-частотную (АЧХ) и фазочастотную характеристики (ФЧХ). АЧХ приведена на рисун-ке 3.5д; из ее анализа следует, что с уменьшением  коэффициент передачи падает. На частоте f = f_н, К = 0.707. Кроме частотных характеристик при анализе цепей важное значение имеет переходная характеристика – это отклик цепи, т.е изменение выходного напряжения во времени при подаче на его вход единичного скачка напряжения. Переходная характеристика для дифференцирующей цепи имеет вид

h(t) = e^-t/ . (3.13)

Вид переходной характеристики для нарастающего напряжения при разных  приведен на рисунке 3.5e. При уменьшении входного напряжения h(t) будет отрицательно.

Если в качестве дифференцирующей используется R-L цепочка, то рассуждения аналогичны предыдущему, только  определяется соотношением

 = L/R . (3.14)

Постоянная времени дифференцирующих цепочек общего применения выбирается обычно в 10 раз меньше длительности фронта мпульса (t_фи), при этом К_n = 0.2  0.4.

На рисунке 3.5ж приведены схемы интегрирующих звеньев. Напряжение на выходе для R-C звена определится соотношением

(3.15)

так как .

Если . (3.16)

Коэффициент передачи интегрирующего звена найдем из выражения

(3.17)

где _в = 2f_в = 1/RC = 1/ – частота, при которой активное и реактивное сопротивления цепочки равны.

Для интегрирующего звена с индуктивностью _в = R/L.

Из (3.16) и (3.17) следует, что с ростом  погрешность интегрирования падает, но при этом и уменьшается выходное напряжение. Амплитудно-частотная и переходная характеристики интегрирующего звена приведены на рисунке 3.5з и рисунке 3.5и.

3.3.3 Цепи из пассивных элементов с резонансными характеристиками

Функциональные узлы, у которых зависимость коэффициента передачи от частоты имеет явно выраженный экстремум, называют цепями с резонансными характеристиками. Они нашли широкое применение в электронных устройствах при создании фильтров, генераторов гармонических колебаний, детекторов и т.д. Наиболее простыми представителями этой группы устройств являются последовательный и параллельный колебательные контуры. Схема последовательного колебательного контура приведена на рисунке 3.6а. Он состоит из последовательно соединенных емкости и индуктивности. Сопротивление r учитывает потери в емкости и индуктивности. Так как емкостное и индуктивное сопротивления зависят от частоты и имеют противоположный характер, то на определенной частоте, называемой резонансной, реактивная составляющая полного сопротивления контура может быть равна нулю и сопротивление контура носит активный характер.

Полное сопротивление контура определяется соотношением

Z = r + j(L - 1/c). (3.18)

Условие резонанса будет выглядеть следующим образом:

L - 1/c = 0; L = 1/c. (3.19)

Из (3.19) находим значение резонансной частоты:

р = 2f_p = 1/ . (3.20)

Характеристическим сопротивлением () называется сопротивление индуктивности или емкости на резонансной частоте:

 = _pL = 1/_pc = . (3.21)

Добротностью контура (Q) называется отношение напряжения на индуктивности (U_L) или емкости (U_C) к напряжению на активном сопротивлении при резонансе:

Q = I/rI = /r. (3.22)

При резонансе амплитуда напряжения на емкости или индуктивности превышает в Q раз амплитуду питающего напряжения (резонанс напряжений).

Величина, обратная добротности, называется затуханием контура:

 = 1/Q . (3.23)

а б в г д

е ж з и

к л м н

а, д – последовательный колебательный контур; е, и – параллельный колебательный контур; к, л – мост Вина; м, н – двойной Т-образный мост.

Рисунок 3.6 – Цепи из пассивных элементов с резонансными

характеристиками

На рисунке 3.6б приведены зависимости реактивного сопротивления контура от частоты, а на рисунке 3.6в зависимость полного сопротивления от частоты. На _p сопротивление минимально и равно r; на частотах выше резонансной сопротивление носит индуктивный характер, а на частотах ниже резонансной – емкостной.

На рисунке 3.6г приведены обобщенные резонансные кривые:

При больших значениях добротности характеристика имеет более ярко выраженный максимум. Важной характеристикой контура является полоса пропускания. Это область частот, в которой I_m/I_mp не меньше заданного значения. Чаще всего полосу пропускания определяют по уровню I_m/I_mp= 1/ = 0,707. Полоса пропускания связана с добротностью следующим соотношением:

f_0.7 = f_p/Q = 2f₁ , (3.24)

где f₁ – абсолютная расстройка по частоте.

На рисунке 3.6д приведена ФЧХ контура. На резонансной частоте фазовый сдвиг равен нулю. На частотах больших резонансной он положительный, но не превышает /2, а на частотах меньших резонансной – отрицательный, но не больше – /2.

На рисунке 3.6е приведена схема параллельного колебательного контура. Свойства его оцениваются теми же параметрами и характеристиками, только рассуждения ведутся относительно проводимостей ветвей, а обобщенная резонансная характеристика определяется как U_m/U_mp = f(). Зависимость проводимости контура от частоты, АЧХ и ФЧХ приведены на рисунках 3.6ж, 3.6з, 3.6и, соответственно. В параллельном контуре токи в ветвях превышают ток неразветвленной части контура в Q раз (резонанс токов).

На низких частотах применение L-C контуров сдерживается увеличением габаритных размеров катушки индуктивности и конденсатора и возрастанием потерь, кроме того, в интегральной схемотехнике применение индуктивных элементов нецелесообразно. В связи с этим разработаны схемы с резонансными характеристиками на элементах R и C. Резонансных явлений в таких схемах не происходит, но АЧХ – ярко выраженный экстремум.

На рисунке 3.6к приведена схема моста Вина. Коэффициент передачи для этой схемы равен

(3.25)

После преобразования (3.25) можно получить

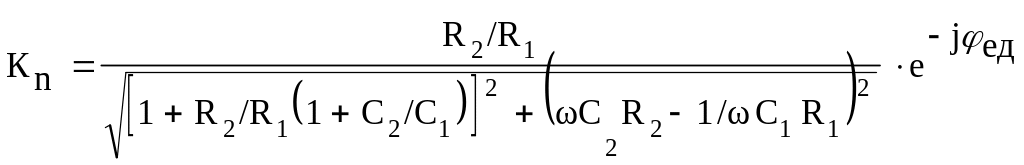
(3.26)

где – фазовый сдвиг.

На частоте ₀ = 1/ (3.27)

фильтр ведет себя, как активное сопротивление (_ед = 0), а коэффициент передачи достигает максимума, равного:

. (3.28)

₀ – называют частотой квазирезонанса.

В частном случае при R₁ = R₂ = R, а С1 = С₂ = С имеем

₀ = 1/RC, а K_nm = 1/3 . (3.29)

АЧХ моста Вина для этого случая приведена на рисунке 3.6л. На рисунке 3.6м приведена схема двойного Т-образного моста. Он также обладает АЧХ, имеющей экстремум (рисунок 3.6н).

При условии R1 ^. C₂ = 4 C₁ ^. R₂ (баланс моста), т.е. при

R₂ =R₁/2 и С₂ = 2С₁, R₁ = R₃, С₁ = С₃ (3.30)

частота квазирезонанса равна:

₀ = 1/R₁C₁. (3.31)

Коэффициент передачи, при выполнении условия (3.30), определяется соотношением

. (3.32)

Использование RC–цепей с резонансными характеристиками позволяет реализовать фильтры, избирательные усилители, генераторы гармонических колебаний в интегральном исполнении.