
- •Функциональные узлы логических и цифровых устройств
- •5.1 Основные логические функции
- •Логическое умножение (конъюнкция), операция "и"
- •Логическое сложение (дизъюнкция), операция "или"
- •Логическое отрицание (инверсия), (операция "не")
- •Основные положения и теоремы алгебры логики
- •Виды логики
- •5.2 Схемная реализация логических элементов
- •5.2.1 Диодно-резисторные схемы
- •5.2.2 Диод-транзисторные схемы
- •5.2.3 Транзисторно-транзисторные схемы
- •5.2.4 Логические элементы на полевых мдп транзисторах
- •5.2.5 Основные параметры логических элементов
- •Контрольные вопросы к разделу 5.1 - 5.2
- •5.3 Триггеры в интегральном исполнении
- •5.3.1 Асинхронный r-s триггер на логических элементах
- •5.3.2 Синхронный r-s триггер
- •Контрольные вопросы к разделу 5.3
- •5.4 Счетчики
- •5.4.1 Двоичный счетчик с последовательным переносом
- •5.4.2 Счетчик с последовательным переносом на вычитание
- •5.4.3 Двоичный счетчик с параллельным переносом
- •5.4.4 Реверсивный счетчик с параллельным переносом
- •5.4.5 Счетчики с произвольным коэффициентом пересчета
- •5.4.6 Двоично-десятичные счетчики
- •Контрольные вопросы к разделу 5.4
- •5.5 Регистры
- •5.5.1 Регистр параллельного типа
- •5.5.2 Последовательный регистр
- •5.5.3 Реверсивный сдвигающий регистр
- •5.6 Дешифратор и шифратор
- •5.6.1 Дешифратор
- •5.6.2 Шифратор
- •5.6.3 Преобразователи кодов
- •5.7 Распределитель (демультиплексор) и мультиплексор
- •5.7.1 Демультиплексор
- •5.7.2 Мультиплексор
- •5.8.2 Операция вычитания
- •5.8.3 Операция умножения цифровых сигналов
- •Контрольные вопросы к разделу 5.8
- •5.9 Устройства для хранения информации (Запоминающие устройства)
- •5.9.2 Оперативные запоминающие устройства (озу)
- •Контрольные вопросы к разделу 5.9
- •5.10 Микропроцессор
- •5.10.1 Общие сведения
- •5.10.2 Микропроцессор к580вм80а
- •Обозначение и функциональное назначение выводов мс.
- •Система команд микропроцессора
- •Команды пересылок
- •Арифметические и логические команды
- •Команды управления
- •5.11 Микропроцессорный комплект (мк)
- •5.11.1 Общие сведения
- •5.11.2 Программируемый параллельный интерфейс кр580вв55а
- •5.11.3. Универсальный программируемый таймер кр580ви53 (ppi)
- •5.11.4 Программирование мк
- •Контрольные вопросы к разделам 5.10 - 5.11
- •Преобразователи сигналов
- •6.1. Ограничители сигнала
- •6.2 Устройства сравнения (нуль-органы)
- •6.3 Выполнение простейших математических операций с сигналами в аналоговой форме Сложение и вычитание
- •Контрольные вопросы к разделам 6.1 - 6.3
- •6.4 Амплитудная модуляция
- •6.5 Амплитудное детектирование
- •6.6 Фазовая и частотная модуляция
- •6.7. Фазовое детектирование
- •6.8 Частотное детектирование
- •Контрольные вопросы к разделам 6.4 - 6.8
- •6.9 Цифро-аналоговые и аналого-цифровые преобразователи
- •6.10 Широтно-импульсный и частотно-импульсный модулятор
Г Л А В А 5
Функциональные узлы логических и цифровых устройств
5.1 Основные логические функции
В последнее время наибольшее распространение получают электронные устройства, в которых в качестве информационного используются импульсные и цифровые сигналы. Функционирование таких систем происходит, как правило, в двоичной схеме счисления, т. е. операции производятся только с двумя числами "0" и "1". Математическим аппаратом, на основе которого реализуются логические и цифровые устройства, является алгебра логики (Булева алгебра). Предметом рассмотрения алгебры логики являются высказывания, которые могут быть либо истинными, либо ложными. Истинность высказывания может принимать, подобно цифрам в двоичной системе счисления, только два значения: истинно – "1", ложно – "0".
Простые высказывания, объединенные логическими связями (операциями), образуют сложное высказывание или логическую функцию. Логическую функцию задают тремя способами: содержательно (путем словесного описания), таблично и алгебраически.
Наиболее наглядный табличный способ записи функции. Таблицы, показывающие связь между входными и выходной (или выходными) величиной, называют таблицами истинности. Рассмотрим основные логические операции.
Логическое умножение (конъюнкция), операция "и"
Содержательное представление функции – сложное высказывание истинно только в том случае, когда истинны все простые высказывания. Алгебраическая запись операции логического умножения имеет вид
y = x1 x2 x3... xn
или (5.1.)
y = x1 * x2 * x3... * xn,
где y – функция;
x1 ... xn – аргументы.
Таблица истинности функции логического умножения для двух переменных приведена на рисунке 5.1а. В таблице истинности приводится значение функции для всех возможных комбинаций значений переменных. Анализируя таблицу истинности, можно заметить, что сигнал на выходе элемента "И" появляется только при наличии "1" на всех входах одновременно, поэтому логический элемент "И" называют схемой совпадения. Условное графическое изображение элемента "И" приведено на рисунке 5.1б.
Х1 |
0 |
1 |
0 |
1 |
Х2 |
0 |
0 |
1 |
1 |
Х3 |
0 |
0 |
0 |
1 |
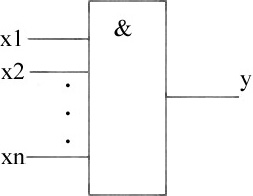
а
б
а – таблица истинности; б – условное графическое обозначение
Рисунок 5.1 – Функция логического умножения (И)
Логическое сложение (дизъюнкция), операция "или"
При логическом сложении сложное высказывание истинно, если истинно хотя бы одно из простых высказываний. Алгебраическая запись операции логического сложения имеет вид:
y = x1 + x2 + x3 ... + xn
или (5.2)
y = x1 v х2 v х3 ... v хn ,
где y – функция;
x1...xn – переменные.
Таблица истинности функции логического сложения для двух переменных, условное графическое обозначение приведены на рисунке 5.2. Из анализа таблицы истинности следует, что сигнал на выходе появляется при наличии сигнала хотя бы на одном из входов, поэтому элемент "ИЛИ" называют сборкой.
Х1 |
0 |
1 |
0 |
1 |
Х2 |
0 |
0 |
1 |
1 |
Y |
0 |
1 |
1 |
1 |
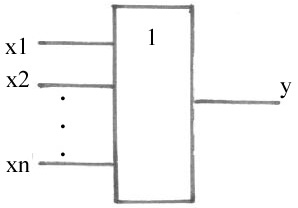
а б
а – таблица истинности; б – условное графическое обозначение
Рисунок 5.2 – Функция логического сложения (ИЛИ)
