2 Исследование шарнирно-рычажного механизма
2.1 Структурный анализ механизма
Определяем степень свободы механизма по формуле Чебышева П.Л. для плоских механизмов:
W=3. n – 2. P5 – P4 = 3 . 5 – 2 . 7 – 0 = 1,
где n – количество подвижных звеньев;
P5 – количество кинематических пар пятого класса;
P4 – количество кинематических пар четвертого класса.
Так как W= 1, то достаточно задать одно начальное звено – звено, закон движения которого задан.
Разбивка на структурные группы Ассура:
6,1-начальный механизм;
2,3-группа Ассура || класса 2-го вида;
4,5-группа Ассура || класса 4-го вида.
В целом заданный механизм является механизмом || класса.
2.2 Кинематическое исследование рычажного механизма
аналитическим методом замкнутого векторного контура
2.2.1 Вывод уравнения перемещений выходного звена
Представим все характерные перемещения в виде векторов. После этого построим замкнутый контур и найдем сумму векторов
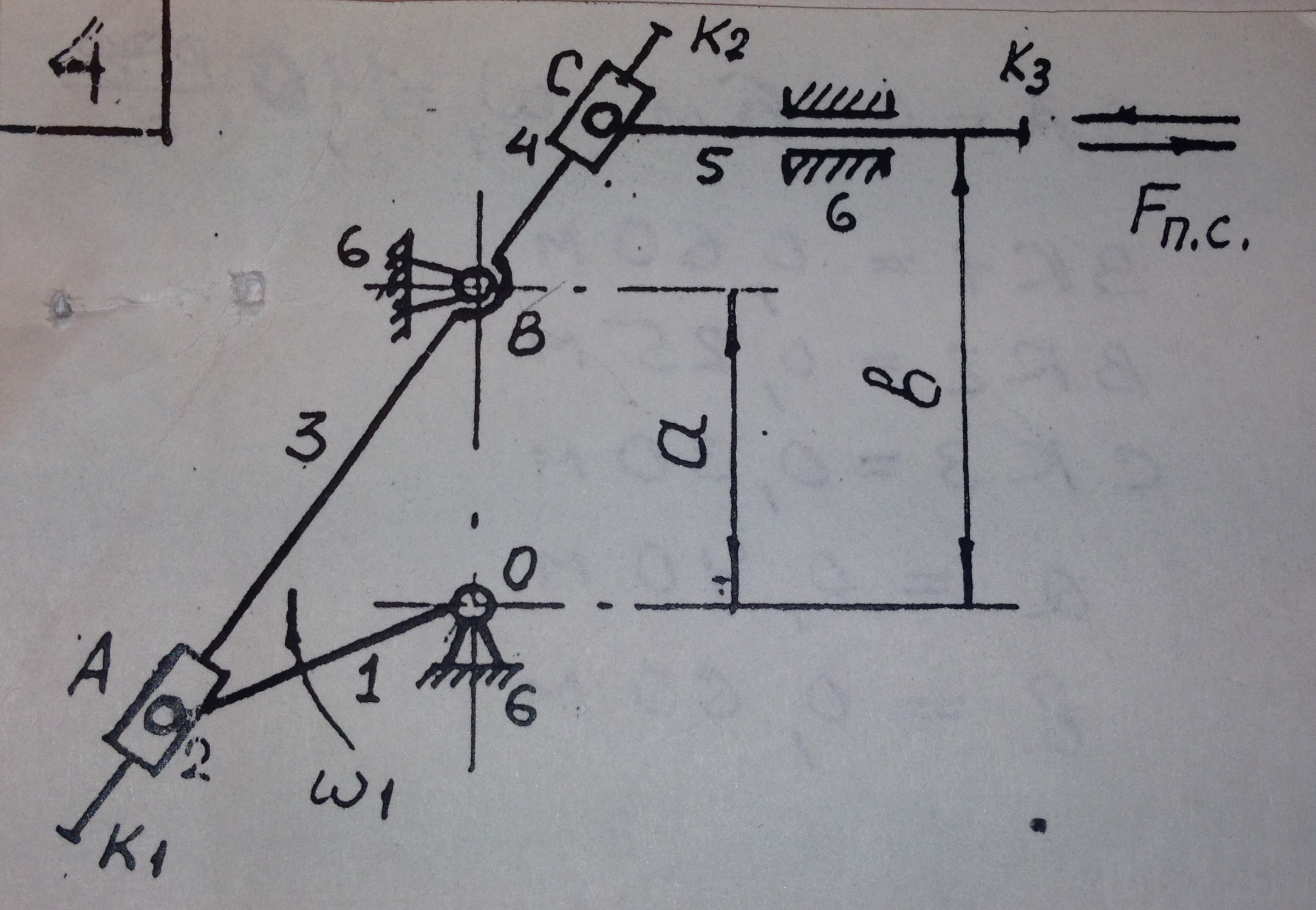
Рисунок 2.1 – Расчётная схема рычажного механизма
1
контур:
.
Поделим одно уравнение на другое:
;
.
2 Контур: ;
(2)
Из
(2)
2.2.2 Определение значений перемещений, скоростей и ускорений
выходного звена с помощью ЭВМ
Для 24 положений механизма с помощью ЭВМ подсчитываем величины угловых перемещений, угловых скоростей и ускорений.
Результаты вычислений приведены на странице 6, там же приведен листинг программы, написанной на языке программирования Basic, с введенными исходными данными для расчёта.
2.3 Кинематическое исследование рычажного механизма
методом планов скоростей и ускорений
Выбираем два следующих положения: №4 и №13.
Вычерчиваем эти положения механизма в масштабе, определенным следующим образом:
Отмерим
отрезок
мм;
м/мм;
Угловая
скорость
во
всех положениях механизма постоянна и
равна
рад/с.
2.3.1 Построение планов скоростей для двух положений и
определение угловых скоростей звеньев
Начальный механизм 6,1
;
м/с;
.
Группа Ассура 2,3 (|| кл. 2 вид)
Примем масштаб:
(м/с)/мм;
,
так как на стойке;
;
;
.
для 4-го положения
;
м/c;
;
м/c.
для 13-го положения
м/c;
м/c.
Группа
Ассура 4,5 (|| кл. 4 вид)
находим
из подобия
отсюда
;
;
;
;
для положения 4:
мм;
м/с;
м/с;
для положения 13:
мм;
м/с;
м/с;
Определение угловых скоростей механизма:
для 4 положения механизма:
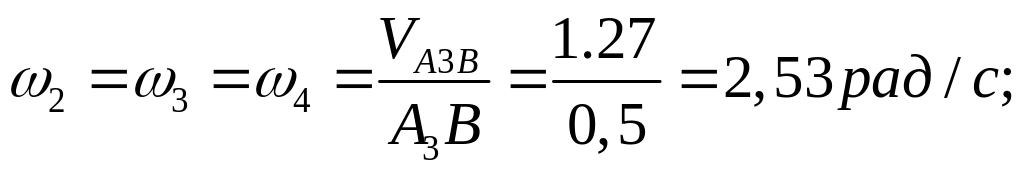
для 13 положения механизма:
2.3.2 Построение планов ускорений для двух положений механизма и
определение угловых ускорений звеньев
;
;
;
;
м/с2;
На плане ускорений откладываем вектор ускорения точки А
мм;
(м/c2)/мм;
Группа Ассура 2,3 (|| кл. 2 вид)
;
для 4-го положения:
Определяем величины угловых ускорений;
.
для 13 положения аналогичным образом получаем
Определяем величины угловых ускорений
;
Группа Ассура 4,5 (|| кл. 4 вид)
;
;
=0;
=0.
для 13 положения аналогичным образом получаем
