Колебательная мощность и электронный к. П. Д.. Влияние нагрузки.
Полная В.Ч. мощность
Pе,
отдаваемая е-пучком в резонатор и
нагрузку, в установившемся режиме может
быть выражена через амплитуду напряжения
и суммарную активную проводимость
зазора
.
;
тогда можно записать:
В установившемся режиме колебаний всегда должно выполняться условие:
Используя формулу:
получаем:
;
где:
.
Выразим величину через параметр группирования Х и учтем что:
;
получим:
.
Мощность, подведенная
к клистрону от источника ускоряющего
напряжения, равна
т. о. из формулы для
м. б. легко определен е-й КПД отражательного
клистрона
.
Обозначим через
и
величины полной колебательной мощности
и электронного КПД в центрах зон
генерации. используя условие:
,
определяющее угол пролета в центрах зоны и пренебрегая углом пролета в высокочастотном зазоре, получим:
.
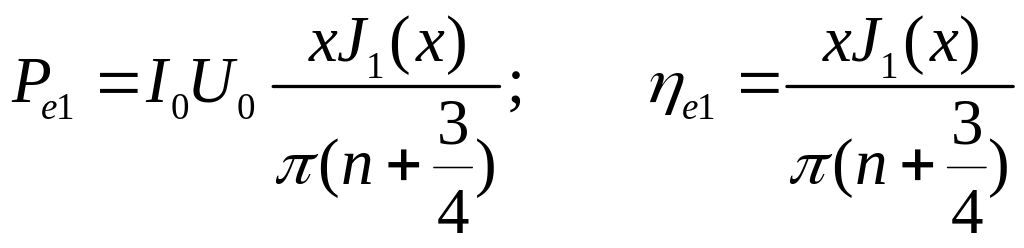Величины
зависят от произведения
.
График функции
приведен на рис. 13
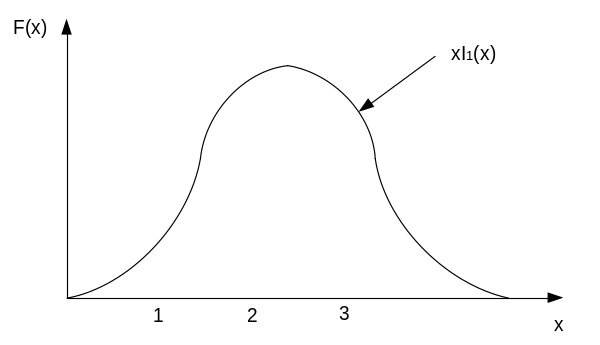
Рис.13.
Эта функция достигает max при х=2,41 т.о. max е-КПД отражательного клистрона для зон с различными номерами равен:
.
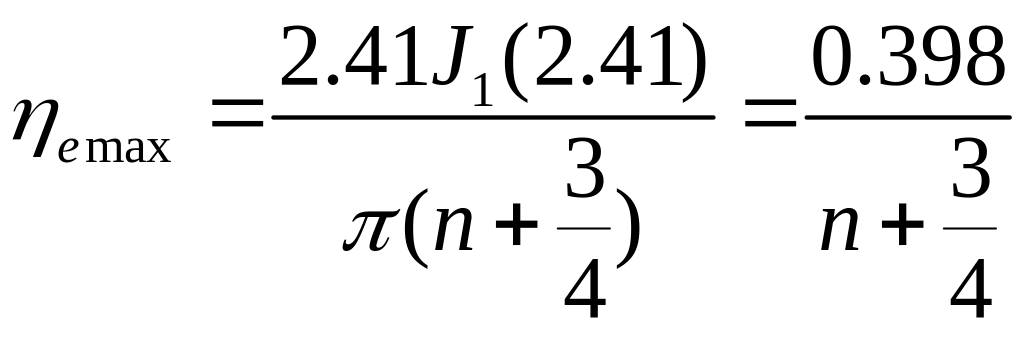В таблице 1 приведены вычисленные по предыдущей формуле значения max КПД для различных зон генерации:
Табл. 1
n |
0 |
1 |
2 |
3 |
… |
7 |
… |
|
53,1 |
22,7 |
14,5 |
10,6 |
… |
5,1 |
… |
,%
При использовании полеченных уравнений, следует помнить, что вся теория
построена на предположении малых амплитуд:
Проверим, как выполняется это условие для различных зон генерации. Вычислим амплитуду , соответствующую opt величине параметра группировки:
Из уравнения:
При x=2,41 имеем:
(
)
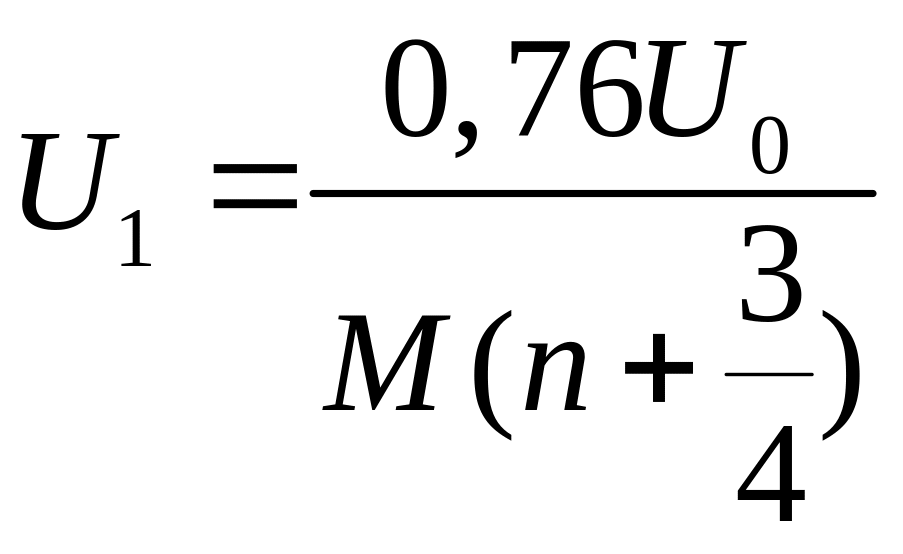В случае M=1
уравнение (
)
дает для «нулевой» зоны (n=0)
величину
равную
.
Этот результат, конечно, несовместим с
исходными допущениями о малости амплитуды
«
»
напряжения в сравнении с ускоряющим
напряжением (т.к чтобы e-ны
не останавливались и не изменяли
направления движения при 2-м прохождении
через зазор, необходимо чтобы:
).
В нулевой зоне при использовании данной
теории не выполняется и это очевидное
физическое требование).
При n=3
амплитуда
,
вычисленная по формуле
,
должна быть равна
,
а при n=6
.
Т.о. данная теория не может быть полностью применена при n=0. Погрешность теории уменьшается при увеличении n.
Исходя из вышеизложенного можно обозначить 2-ве особенности работы отражательных клистронов:
В отличие от УК e-КПД ОК в разных зонах генерации неодинаков и уменьшается с ростом зоны n. Соответственно этому чем меньше по абсолютной величине , тем ниже мощность, генерируемая ОК в центре зоны.
Максимальный e-КПД ОК оказывается значительно ниже, чем у УК.
Такой результат можно объяснить с физической точки зрения. Основной причиной малого e-КПД является то, что скоростная модуляция e-пучка и отбор энергии производится одним и тем же зазором и, следовательно, при одном и том же напряжении. При большом угле пролета амплитуда модулирующего напряжения должна быть малой и уменьшаться с ростом n, что неизбежно приводит к уменьшению колебательной мощности даже при оптимальном режиме группировки.
Кроме режима e-КПД
и max
Pe,
характеризуемого условием: x=2,41
можно рассмотреть режим полного КПД
.
Величина
определяется, как обычно, произведением
«контурного» КПД с учетом потерь в
резонаторе. Величина параметра
группирования X,
в данном случае, немного отличается от
найденного opt
значения и в зависимости от активной
проводимости резонатора ОК лежит в
пределах:
2,41≥x≥1,84
В расчетах не учитывалось снижение КПД за счет оседания e-нов на сетках при 1-м и 2-м прохождении через резонатор. Практически, с учетом оседания e-нов, СВЧ потерь в резонаторной системе и других факторов полный КПД даже в opt зоне генерации не превышает 1-3 %.
Нагрузка очень сильно влияет на работу резонатора. Не следует путать max мощность, отдаваемую в резонатор и max мощность, отдаваемую в нагрузку. Чтобы получить max P в нагрузке подбирают opt связь между резонатором и нагрузкой. Opt
нагрузка при которой P, отдаваемая в нагрузка достигает наибольшего значения, показана на рис.9.
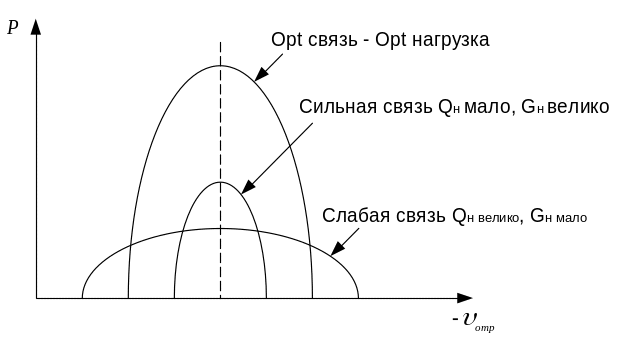
Рис.14
На рис.15 показана зависимость мощности от величины амплитуды напряжения между сетками резонатора:
-мощность, которая отдается в резонатор
– мощность потерь
в резонаторе.
– выходная мощность
ОК – разность между
и
.
Из рис.15 видно, что
max
мощность, отдаваемая в резонатор, и max
выходная мощность не совпадают: выходная
максимальная мощность несколько дальше,
чем
.
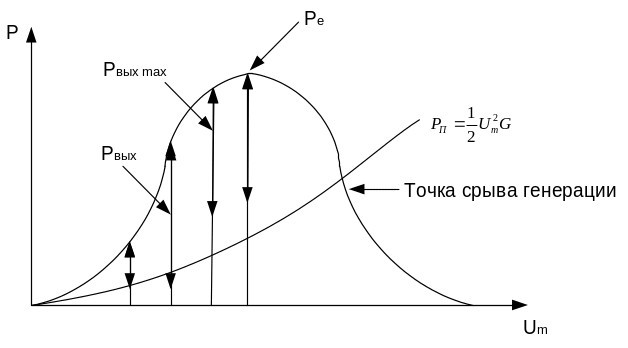
Рис.15