Тема: “Елементи математичної статистики. Довірчі (надійні) інтервали”

117. З великої партії електролампочок було відібрано у випадковому порядку 400 штук для визначення середньої тривалості горіння. Вибіркове середнє тривалості горіння лампочки виявилось рівним 1220 годин, а вибіркове стандартне відхилення – 35 годин. Визначити з імовірністю 0,95 надійний інтервал для середньої тривалості горіння лампочки в усій партії.

118. Для визначення середнього вмісту сирого білку в зернах пшениці було випадково відібрано 625 зерен. Їхнє обстеження показало, що вибіркове середнє дорівнює 16,8, а вибіркова дисперсія – 4. Визначити з імовірністю 0,95 надійний інтервал для середнього процентного вмісту сирого білку.

119. Обстежено 800 корів, які знаходяться в особистому володінні селян деякого району. Виявили, що середній річний надій від однієї корови складає 2800 кг, а вибіркове стандартне відхилення становить 250 кг. Визначити з імовірністю 0,95 надійний інтервал для середнього річного надою від однієї корови в усьому районі.

120. Проведено вибіркове вимірювання денного виробітку на земляних роботах у 144 робітників. Визначено, що середній виробіток становить 4,95 куб. м, а вибіркове стандартне відхилення дорівнює 1,5 куб. м. Визначити з імовірністю 0,95 надійний інтервал для середнього денного виробітку.

121. Верстат-автомат штампує валки. За вибіркою об‘ємом 100 штук встановлено, що їхній середній діаметр дорівнює 102 мм, вибіркове стандартне відхилення - 2мм. Визначити з імовірністю 0,95 надійний інтервал для середнього діаметра в усій партії виготовлених валків.

122. Проведено вибіркове обстеження продукції шліфувального верстата. Вимірюванням товщини 400 виготовлених пластин встановлено, що їхня середня товщина дорівнює 2,15 мм, а вибіркове стандартне відхилення - 0,04. Визначити з імовірністю 0,95 надійний інтервал для середньої товщини в усій продукції верстата.

123. Для визначення схожості зерна було сформовано вибірку з 500 зерен, з яких проросло 478. Визначити з імовірністю 0,95 надійний інтервал для процента схожості зерна.

124. З виготовленої продукції було взято вибірку з 400 виробів, в якій виявилися 6 бракованих виробів. Визначити з імовірністю 0,95 надійний інтервал для процента бракованих виробів в усій продукції.

125. Для визначення процента виробів другого сорту в усій партії взято випадкову вибірку об‘єму 300 одиниць. Визначити з імовірністю 0,95 надійний інтервал для проценту виробів другого сорту в усій партії, якщо у вибірці виявилося 75 таких виробів.

126. Вибірково обстежено якість цегли. З 1600 проб в 32 випадках цегла виявилася бракованою. Визначити з імовірністю 0,95 надійний інтервал для процента бракованих виробів в усій продукції.

127. Під час перевірки 10000 волокон з партії льону виявилося 1200 недозрілих. Визначити з імовірністю 0,95 надійний інтервал для долі недозрілих волокон в усій партії льону.

128. У 500 радіоламп даного типу було в заданих умовах перевірено силу анодного струму, причому у 150 вона виявилася вищою за ту, яка гарантується паспортом. Визначити з імовірністю 0,95 надійний інтервал для долі таких ламп в усій партії.

Основні формули

Ймовірність випадкової події : Р(А) =

Ймовірність суми подій:

Ймовірність добутку подій:

Ймовірність появи принаймні однієї події з двох незалежних подій:

Формула повної ймовірності:

Формули Баєса:

Формула Бернуллі:

Найбільш ймовірна кількість успіхів (мода):

Локальна формула Муавра-Лапласа:

Інтегральна формула Муавра-Лапласа:

Формула Пуассона:

Математичне сподівання випадкової величини дискретної неперервної

Початковий момент k-го порядку випадкової величини дискретної

неперервної

Дисперсія випадкової величини D(Х) = М(Х - М(Х))²

Розрахункова формула для дисперсії D(Х) = М(Х²) - (М(Х))²

Стандартне відхилення випадкової величини

Ймовірність попадання нормальної випадкової величини в

заданий інтервал Р( < X < ) = Ф

Ймовірність відхилення нормальної випадкової величини від п середнього значення

<

Вибіркове середнє: , або х_в =

Вибіркова дисперсія: або

Виправлена вибіркова дисперсія:

Вибіркове стандартне відхилення:

Умовні початкові моменти:

Вибіркове середнє і дисперсія через умовні початкові моменти:

Довірчий інтервал для математичного сподівання:

Довірчий інтервал для стандартного відхилення:

Довірчий інтервал для ймовірності: або , де

Статистика критерію для дисперсій:

Статистика критерію для середніх

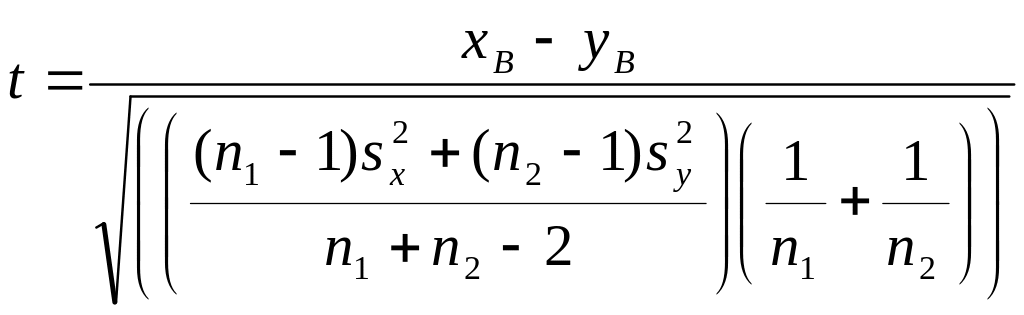
Статистика критерію для ймовірностей

Статистика критерію Пірсона

Вибіркове рівняння прямої лінії регресії